
Yes, you read that correctly. Not the Greenhouse Effect – the Green Plate Effect.
The Green Plate Effect is an analogy to the Greenhouse Effect, introduced by blogger Eli Rabett back in 2017. He begins his post with the following paragraph:
An evergreen of denial is that a colder object can never make a warmer object hotter. That's the Second Law of Thermodynamics, so according to the Agendaists, the Greenhouse Effect, with greenhouse gases playing the role of the colder object, is rubbish. They neglect the fact that heating and cooling are dynamic processes and thermodynamics is not.
Skeptical Science has had a link to Eli’s excellent post since it first appeared in October 2017 – at the bottom of the “Greenhouse effect and the 2nd law of thermodynamics” rebuttal. Yet here we are, over five years later, and we still see people arguing on the SkS 2nd law post that the process of atmospheric absorption and re-radiation cannot heat the surface because the atmosphere is colder than the surface. It truly is an evergreen of denial.

Figure 1: Would a large, green plate that captures and re-radiates the infra-red energy loss from the astronaut actually help warm the astronaut up? Yes, and it can do so even if the green plate receives no solar heating. Illustration by jg.
So, since we’re still sending people to Eli’s to read The Green Plate Effect, we’ve decided to provide a summary here, along with some additional results of a dynamic version – the progression of temperatures and radiation fluxes over time as The Green Plate Effect approaches equilibrium. This way, we can shift discussion of this specific topic off the 2nd law thread (which has now accumulated over 1500 comments) and provide a place where comments are active – rather than just pointing people to Eli’s and hoping they read and learn.
...but that’s not to say that reading Eli’s original post is not worth it. We’re only summarizing it here, and then adding some additional analysis – but the original is more complete in its derivation. (Make sure you put on your head vice before you read the comments, though.)
The Greenhouse Effect in the earth-atmosphere system stipulates that visible light from the sun heats the earth’s surface with little atmospheric absorption, and then the surface radiates IR radiation back upwards. Much of that upward-directed IR radiation is absorbed by the atmosphere, rather than being lost directly to space. And when the atmosphere re-radiates IR radiation, it does it in both upward and downward directions. The downward-directed IR then needs to be absorbed and re-radiated again, and may need to go through that cycle several times before being finally lost to space. In the end, global absorbed solar radiation balances IR radiation lost to space. With an atmosphere that absorbs IR radiation, this occurs with a higher surface temperature than it would without an atmosphere. This heating effect (a higher surface temperature caused by an overlying cooler atmosphere) is where the evergreen of denial that Eli mentions kicks in. People seem to think that the fact that the atmosphere is colder than the surface (it is) makes it impossible for it to have any effect that leads to a warmer surface (but it does).
Eli’s Green Plate Effect analogy take a much simpler system than the earth-atmosphere system, but it clearly demonstrates the errors in the ‘but the atmosphere is colder” argument. Rather than a spherical earth lit up by the sun, Eli postulates a single plate that receives 400 W/m2 from the sun on one side. The plate absorbs all of that radiation, so on the non-sunny side of the plate, there is no radiation from the sun. Here is Eli’s first figure illustrating the system: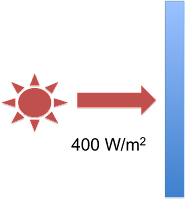
Figure 2: The single Blue Plate system - figure 1 from Eli Rabett's Green Plate Effect post.
Once the plate starts to warm up, it will emit radiation itself – and it will be emitted from both sides, not just the sunlit-side. When it heats up to the point where emitted radiation equals absorbed radiation, it will stop heating. At that point, the system fluxes will be as illustrated in Eli’s second figure:
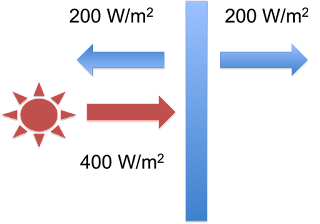
Figure 3: The single Blue Plate system at equilibrium - figure 2 from Eli Rabett's Green Plate Effect post.
From the Stefan-Boltzman Law (E=σT4), Eli points out that the plate will have a temperature of 244K.
Then, Eli introduces a second plate – the Green Plate. [Cue dramatic music.] This is located to the right of the first plate – so it is blocked from the sun. The only radiation it receives is the flux emitted from the right side of the first plate (the Blue Plate). Eli goes through more of the derivation to get to his fifth figure, which shows the temperatures and fluxes with the additional Green Plate:
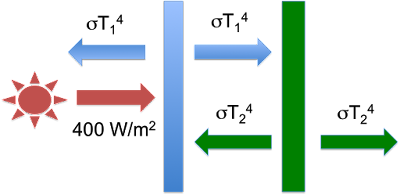
Figure 4: The Green Plate Effect system - figure 5 from Eli Rabett's Green Plate Effect post.
With a little additional algebra, Eli shows that the new equilibrium temperature of the Blue Plate will be 262K – a temperature 18K higher than when there was no Green Plate. Eli does not mention it, but at equilibrium the temperature of the Green Plate is 220K. So there it is: even though the Green Plate is cooler than the Blue Plate, it’s presence and re-radiation leads to a warmer Blue Plate. Just like the cooler atmosphere’s counter-radiation leads to a warmer earth surface temperature.
The Green Plate model is a simple energy balance model. It relies on the Stefan-Boltzman law to determine the radiation emitted from each side of each plate, but there is no violation of the 2nd law of thermodynamics. The Green Plate Effect is enough to clearly demonstrate that the presence of a cooler body will alter the radiative balance of another body (the Blue Plate) and cause an increase in the temperature of that body.
Eli only explicitly does the calculations for the equilibrium condition. Eli himself states “the entire system has to heat up to reach the equilibrium condition”, but he does not provide calculations showing how the temperature or radiation balance of each plate changes during that period. That is not hard to do, though, so we’ll do it here.
In The Green Plate system, at equilibrium the entire system and the two individual plates have the following energy balances:
For the entire system, we have the solar input equalling the amount emitted to the left of the Blue Plate plus the amount emitted to the right of the Green Plate. (The exchanges in between the two plates are completely internal to the system.)
400 W/m2 = σ T14 + σ T24
For the Blue plate, we have the solar input plus the input from the left side of the Green Plate equalling the amounts emitted from both sides of the Blue Plate:
400 W/m2 + σ T24 = 2 σ T14
For the Green Plate, we have the input from the right side of the Blue Plate equalling the amounts emitted from both sides of the Green Plate:
σ T14 = 2 σ T24
These equalities are what Eli used to determine the equilibrium temperature of the Blue Plate: 262K in the presence of the Green Plate, versus 244K without it.
What about conditions when the system is not at equilibrium? We can use those same equations, but we do a bit of rearranging to get:
For the entire system,
Net energy input = 400 W/m2 - ( σ T14 + σ T24 )
For the Blue plate,
Net energy input = 400 W/m2 + σ T24 - 2 σ T14
For the Green Plate,
Net energy input = σ T14 - 2 σ T24
In order to translate the net energy input for each plate into a temperature change, we need to specify the heat capacity of each. If we choose 400 as a value (I’ll let you figure out the units), we’ll have a system where a net input of 400 W/m2 will lead to a 1K rise in temperature in 1 second. (They are thin plates.) With this, our equation for temperature change in each plate is:
ΔT = net energy input / 400
This system is easy to set up in a spreadsheet. If we do this, and start each plate at a temperature of 0K, this is how the temperatures change over time:
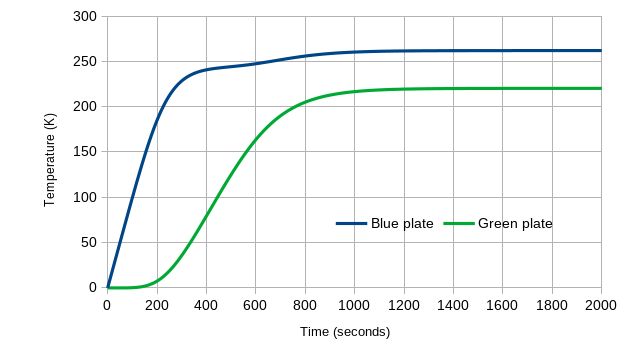
Figure 5: the temperature evolution of the Green Plate Effect starting at 0K, to equilibrium
After roughly 1200 seconds, we see that the two plates have more or less reached equilibrium, at the temperatures that Eli’s algebra said they would. We also see several other interesting characteristics:
We also can learn more by looking at the absorbed energy input for each plate over time. At the start, the Blue Plate only absorbs the 400 W/m2 from the sun, and the Green Plate is getting nothing – it is shaded from the sun, and the Blue Plate (at 0K) is not emitting anything towards the Green Plate. As the system warms, the Green Plate starts to get input from the Blue Plate, and the Blue Plate has the back-radiation from the Green Plate added to the sun’s 400 W/m2. At equilibrium, the Blue Plate is receiving a total of 533 W/m2 (400 W/m2 from the sun plus 133 W/m2 from the Green Plate). That’s a 33% increase – no wonder it is warmer! We also see that the Green Plate always absorbs less radiation than the Blue Plate.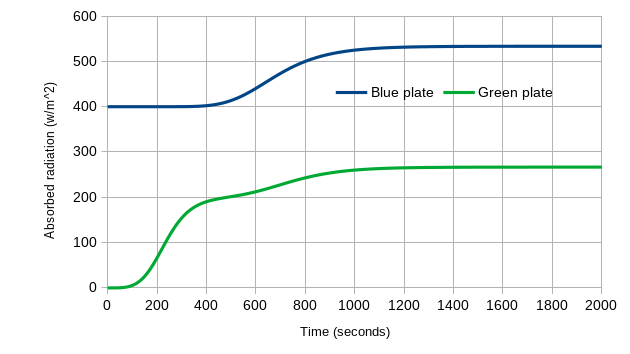
Figure 6: Absorbed radiation versus time, for the Green Plate Effect as it goes from 0K to equilibrium
We can also look at the net radiation for each plate: the inputs (above) minus the amount each plate emits. The Blue Plate starts at 400 W/m2 (the sun’s input), and as it warms up and emits radiation, the net radiation drops – eventually reach zero at equilibrium. For the Green Plate, it initially has zero input and zero emissions for net zero, then net radiation rises as the Blue Plate warms and emits more, and then as the Green Plate warms its net radiation drops – also reaching zero at equilibrium.
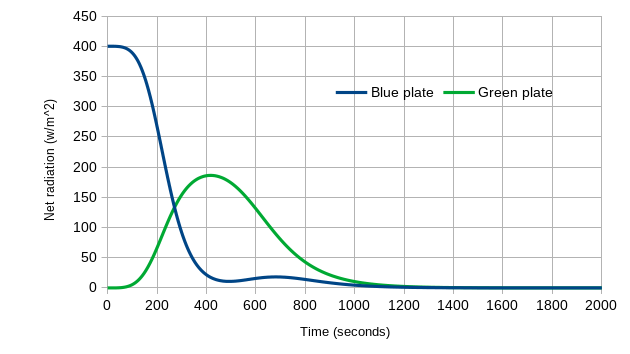
Figure 7: Net radiation versus time, for the Green Plate Effect as it goes from 0K to equilibrium
So, there you have it – a dynamic view of Eli’s Green Plate Effect. A cool object (the Green Plate, heated by the warmer Blue Plate) leads to an even warmer Blue Plate. Just as a cool atmosphere (heated by the warmer earth’s surface) leads to an even warmer surface.
To paraphrase Eli’s closing comment on his blog post:
Show this to the next person with an agenda who thinks that the Green Plate Effect [or Greenhouse Effect] violates the Second Law of Thermodynamics
Additional Information
The single-plate example should be enough to dissuade anyone from arguing that a cool object cannot have a warming effect on a warmer object. The Single Green Plate model is very simplistic compared to the earth-atmosphere system, though. Do you want to see what happens if additional plates are added to Eli’s Green Plate Effect? Eli has a later post for that scenario. Spoiler alert: adding more plates increases the warming effect.
Not convinced that this relates to the Greenhouse Effect in the earth-atmosphere system? Eli has a post for that, too. Spoiler alert: adding more gases that absorb IR radiation increases the warming effect.
Prefer to read about these things in published sources such as books? A model similar to Eli’s multi-layer models can be found in John Harte’s 1988 book Consider a Spherical Cow. No publisher’s page that I can find (I have a paper copy), but a search will find it listed at many book stores and libraries.
Supplemental Data
If you would like to play around with the calculations that generated figures 5-7, you can download this CSV file that includes the numbers and equations for the dynamic Green Plate Effect model. This is a plain text file that can be opened/imported into any common spreadsheet program. You will need to set up your own graphs after importing the file. The equations are set up so that you can easily change the solar input, plate heat capacities, and time step.
Posted by Bob Loblaw on Wednesday, 28 June, 2023
 |
The Skeptical Science website by Skeptical Science is licensed under a Creative Commons Attribution 3.0 Unported License. |