CO2 emissions change our atmosphere for centuries
What the science says...
Individual carbon dioxide molecules have a short life time of around 5 years in the atmosphere. However, when they leave the atmosphere, they're simply swapping places with carbon dioxide in the ocean. The final amount of extra CO2 that remains in the atmosphere stays there on a time scale of centuries.
Climate Myth...
CO2 has a short residence time
"[T]he overwhelming majority of peer-reviewed studies [find] that CO2 in the atmosphere remained there a short time." (Lawrence Solomon)
The claim goes like this:
(A) Predictions for the Global Warming Potential (GWP) by the IPCC express the warming effect CO2 has over several time scales; 20, 100 and 500 years.
(B) But CO2 has only a 5 year life time in the atmosphere.
(C) Therefore CO2 cannot cause the long term warming predicted by the IPCC.
This claim is false. (A) is true. (B) is also true. But B is irrelevant and misleading so it does not follow that C is therefore true.
The claim hinges on what life time means. To understand this, we have to first understand what a box model is: In an environmental context, systems are often described by simplified box models. A simple example (from school days) of the water cycle would have just 3 boxes: clouds, rivers, and the ocean.
A representation of the carbon cycle (ignore the numbers for now) would look like this one from NASA.
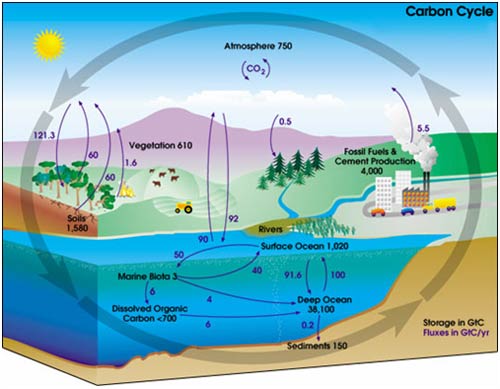
In the IPCC 4th Assessment Report glossary, "lifetime" has several related meanings. The most relevant one is:
“Turnover time (T) (also called global atmospheric lifetime) is the ratio of the mass M of a reservoir (e.g., a gaseous compound in the atmosphere) and the total rate of removal S from the reservoir: T = M / S. For each removal process, separate turnover times can be defined. In soil carbon biology, this is referred to as Mean Residence Time.”
In other words, life time is the average time an individual particle spends in a given box. It is calculated as the size of box (reservoir) divided by the overall rate of flow into (or out of) a box. The IPCC Third Assessment Report 4.1.4 gives more details.
In the carbon cycle diagram above, there are two sets of numbers. The black numbers are the size, in gigatonnes of carbon (GtC), of the box. The purple numbers are the fluxes (or rate of flow) to and from a box in gigatonnes of carbon per year (Gt/y).
A little quick counting shows that about 200 Gt C leaves and enters the atmosphere each year. As a first approximation then, given the reservoir size of 750 Gt, we can work out that the residence time of a given molecule of CO2 is 750 Gt C / 200 Gt C y-1 = about 3-4 years. (However, careful counting up of the sources (supply) and sinks (removal) shows that there is a net imbalance; carbon in the atmosphere is increasing by about 3.3 Gt per year).
It is true that an individual molecule of CO2 has a short residence time in the atmosphere. However, in most cases when a molecule of CO2 leaves the atmosphere it is simply swapping places with one in the ocean. Thus, the warming potential of CO2 has very little to do with the residence time of individual CO2 molecules in the atmosphere.
What really governs the warming potential is how long the extra CO2 remains in the atmosphere. CO2 is essentially chemically inert in the atmosphere and is only removed by biological uptake and by dissolving into the ocean. Biological uptake (with the exception of fossil fuel formation) is carbon neutral: Every tree that grows will eventually die and decompose, thereby releasing CO2. (Yes, there are maybe some gains to be made from reforestation but they are probably minor compared to fossil fuel releases).
Dissolution of CO2 into the oceans is fast but the problem is that the top of the ocean is “getting full” and the bottleneck is thus the transfer of carbon from surface waters to the deep ocean. This transfer largely occurs by the slow ocean basin circulation and turn over (*3). This turnover takes 500-1000ish years. Therefore a time scale for CO2 warming potential out as far as 500 years is entirely reasonable (See IPCC 4th Assessment Report Section 2.10).
Intermediate rebuttal written by Doug Mackie
Update July 2015:
Here is the relevant lecture-video from Denial101x - Making Sense of Climate Science Denial
Last updated on 5 July 2015 by pattimer. View Archives































 Arguments
Arguments

































And like a bad penny, this silly argument has risen again. Someone named Gosta Petterson (a professor emeritus of biochemistry and specialist in reaction kinetics, not atmosphere or carbon cycle) is once again claiming that individual molecular residence time (one way) is somehow identical to CO2 concentration change time (with most CO2 molecules simply exchanging for another from a different climate compartment), a much slower process.
There's a good discussion of this topic and the errors involved on SkS, under The Independence of Global Warming on Residence Time of CO2.
Sadly, this appears to be yet another example of an emeritus professor wandering out of his specialty, and with little perspective proclaiming an entire field of science invalid. And of long-debunked myths being recycled over and over again...
"Biological uptake (with the exception of fossil fuel formation) is carbon neutral: Every tree that grows will eventually die and decompose, thereby releasing CO2. "
I can see how that would be true for the portion of a tree above ground (assuming the wood isn't used to make a house or something that locks up the wood for 100+ years), but my impression is that the roots are probably as large a carbon sink as the above ground tree and that the smallest tendrils will constantly grow and die back and essentially become part of the soil, fixing their carbon for a long time. Do you have a paper that supports your assertion that trees/plants are carbon neutral? (Preferably one that actually measures the carbon fixing of below ground material over time.) It seems unlikely to be carbon neutral.
This paper argues that organic carbon stored in forest soils are a reservoir roughly the same size as the atmosphere, so we aren't talking about a small effect. http://www.dpi.nsw.gov.au/__data/assets/pdf_file/0006/389859/Principles-and-Processes-of-Carbon-Sequestration-by-Trees.pdf
Ashby, there are fungi and bacteria in the soil that break down the roots of dead trees as well. I suspect how fast this happens depends on the moisture and oxygen availability. If this were not true, we would be digging up the roots of dead trees everytime we dig a hole in the ground, which is not the case.
Ashby @145, according to Melin et al (2009), root systems apparently account for only 20% of the biomass of a tree (citing Hakilla, 1989). Further, for Norway Spruce, 4.6% of the subterainian biomass decomposes per year, so that 50% is lost in 15 years, and 95% in 64 years. That is faster than the 3.8% of soil carbon respired to the atmosphere each year (see diagram in main article), but not sufficiently so as to expect a large increase in the soil reservoir from reforestation relative to the increase in the vegetation reservoir from the growth of the trees.
Below-surface carbon in forest can be quite complex. I say "below-surface" because there is not only roots, but also carbon in other soil micro-organisms, plus carbon from decaying roots, etc., as well as the carbon that is carried into the soil from surface litter and such.
Roots do decay over periods of years to centuries, depending on size (and what forect type you are talking about). Tree trunks and branches fall to the forest floor, and then slowly rot - but the more persistent carbon compounds produced will work their way into the soil.
In tropical forests, soil carbon and surface litter are rapidly decayed, so soil carbon content is low - root mass will be the dominant store. In the boreal forest, soild carbon often exceeds (per hectare) the carbon stored in trees above ground, due to cooler temperatures and slow decay rates.
Fire obviously returns carbon rapidly back to the atmosphere, as biomass is burned. Removal of above-ground mass (burning, logging, etc.) will often lead to a rapid drop in soil carbon, as the soil is exposed to sunlight and warmer temperatures. The loss of soil carbon often exceeds the uptake by new growth, so a rapidly-growing forest in a recently-disturbed area can still be a source of carbon (loss to atmosphere), not a sink.
Turning lumber into houses and such does represent a moderate-term carbon sink. Carbon budget models of the forest will account for these factors, such as the Canadian Carbon Budget Model.
I'm most familiar with the dynamics of boreal forests. One major study from 20 years ago was the BOREAS project. A Google search for "BOREAS soil carbon" gives megahits.
Forests do represent major carbon storage, and that is where some of the carbon from burning fossil fuels is going, but by and large they do not represent a long-term permanent sink.
Hi, the question I have is how do we know that global CO2 emissions weren't increasing at a rate of 3.3x back before the industrial revolution? (Sorry forgot the units). If so, how did the process of figuring that out work?
Thank you.
[Rob P] - There are multiple lines of evidence, but the simplest to understand is that tiny bubbles of air are trapped in snow on the giant ice sheets of Antarctica and Greenland. As this snow is slowly compacted to form ice, the air trapped inside is sealed off from the atmosphere. The ice that has survived for hundreds of thousands of years is therefore a continuous record of the Earth's atmosphere. Core samples are obtained by drilling down into the ice with specialized drilling rigs, and the ice core is later painstakingly analyzed to determine atmospheric CO2 concentration.
Consider the last 10,000 years for instance.......
Tom Curtis' Climate Change Cluedo is also a worthwhile read if you want to learn more.
Zadams @149, I assume you are asking how do we know that atmospheric CO2 was not increasing by 3.3 Gigatonnes of Carbon per annum (1.56 ppmv) prior to the industrial revolution?
Well, to start with, the increase in CO2 concentration observed at Hawaii shows an accelerating trend:
Decade Total Increases Average Annual Rates of Increase
2005 – 2014 21.06 ppm 2.11 ppm per year (4.47 GtC per year)
1995 – 2004 18.67 ppm 1.87 ppm per year (3.96 GtC per year)
1985 – 1994 14.24 ppm 1.42 ppm per year (3.01 GtC per year)
1975 – 1984 14.40 ppm 1.44 ppm per year (3.05 GtC per year)
1965 – 1974 10.56 ppm 1.06 ppm per year (2.25 GtC per year)
1960 – 1964 3.65 ppm 0.73 ppm per year (5 years only) (1.55 GtC per year)
Second, CO2 data from icecores, and C13 data from icecores, speliothems, corals, and mollusc shells show CO2 levels to have been near constant prior to 1750 going as far back as the end of the last glacial. I discuss these in a post here that canvasses the wide range of evidence showing the recent increase in CO2 to have been anthropogenic (see in particular points 1, 5 and 10).
However, the most fundamental reason is arithmetic. The atmosphere currently has about 400 ppmv of CO2 (848 GtC). If atmospheric CO2 had been increasing continuously by 3.3 GtC per annum into the past, just 257 years ago, the atmosphere would have had no CO2 (at which point there could be no photosynthesis, and hence no plants on which we live). Even an increase of as little as 0.09 GtC per year would mean that at the start of the phanerozoic, at the time humans were inventing agriculture, there would have been no CO2 and hence no possibility of our wheat, rye, rice or maize growing. So, even if we had no CO2 records going back into the past, we would know that the current rate of increase is much greater than fifty times the long term average rate of increase leading into the industrial revolution.
So, if we want to believe that the increase in CO2 is natural in origin, we need to believe that just as the industrial revolution kicked of, the long term natural rate of net emissions suddenlty increased by a factor of 10 or more, and then continued to increase over the following 250 years in almost perfect sync with know human emissions until they rose to their current level of well over fifty times the previous long term rate of increase. Further, at the same time we have to believe their is an independent natural sink that did not previously operated that increased at the same rate as human emissions to nullify them, and which is triggered by those emissions so that it should not be included in the net natural emissions, is also incapable of stabilizing net natural emissions (which on this scenario are anything but stable). Put simply, that is not an elegant hypothesis.
Finally, FYI, from icecore data we know that the long term increase in CO2 over the holocene up to the industrial revolution was actually about 0.004 GtC per annum; and there is good reason to think that most of that was driven by deforestation driven by the expansion of agriculture (ie, that it was anthropogenic).