Climate time lag
Posted on 8 July 2009 by John Cook
The previous post on CO2/Temperature correlation sparked some interesting comments on climate time lag. Unfortunately, the discussion went pear shaped with some ideological anti-intellectualism and things got a little bitchy after that. Nevertheless, climate time lag is an important subject that deserves more attention. Several metaphors were invoked in an effort to explain the phenomenon including stove hot plates and warming baths. However, I find the best way to understand climate time lag is a direct look at the science.
Our climate receives its energy from the sun. The amount of energy the planet absorbs from the sun is calculated from this equation:
Incoming Energy Flux= πR2S(1-A)
R is the radius of the earth, S (the solar constant) is the energy flux from the sun and A is the Earth's albedo - around 30% of sunlight is reflected back to space. The earth also radiates energy into space. The amount of energy emitted is a function of its temperature:
Outgoing Energy Flux = 4πR2εσT4
σ is Boltzmann's constant, T is the absolute temperature in degrees Kelvin and ε is the average emissivity of the earth. Emissivity is a measure of how efficiently the earth radiates energy, between 0 and 1. A blackbody has an emissivity of 1. Greenhouse gases lower the earth's emissivity. When the climate is in equilibrium, energy in equals the energy out.
S(1-A) = 4εσT4
What happens if the sun warms (solar constant S increases) then maintains a sustained peak? This is what occured in the early 20th century when solar levels rose then plateaued at a hotter state in the 1950's. The radiative forcing from the warming sun is not particularly large - between 0.17 W/m2 (Wang 2005) to 0.23 W/m2 (Krivova 2007) since the Maunder Minimum. Nevertheless, let's assume for the sake of argument that there is some amplifying effect (perhaps the cosmic ray effect on clouds) so that the warming sun has a substantial effect on global temperature.
When the sun warms, initially more solar energy is coming in than is radiating back out. The earth accumulates heat and it's temperature rises. As the earth warms, the amount of energy radiating back out to space increases. Eventually, the energy out matches the incoming solar energy and the planet is in equilibrium again. The time lag is how long it takes climate to return to equilibrium.
How long does the climate take to return to equilibrium? The lag is a function of climate sensitivity. The more sensitive climate is, the longer the lag. Hansen 2005 estimates the climate lag time is between 25 to 50 years.
How would climate have responded to the solar levels maxing out in the 50's? For the next few decades after the 50's, the radiative imbalance would've gradually decreased until the climate reached radiative equilibrium around the late 80's (give or take a decade). So how has our planet's radiative imbalance evolved over the latter 20th century?
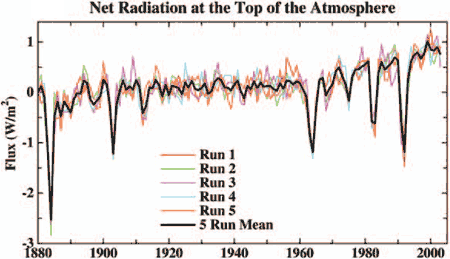
Figure 1: net radiation flux at the top of the atmosphere (Hansen 2005).
Hansen 2005 finds that the net radiative imbalance has steadily increased over the 20th century. There is no indication that the climate is heading towards equilibrium - quite the contrary. This is confirmed by satellite measurements of energy flux at the top of the atmosphere:
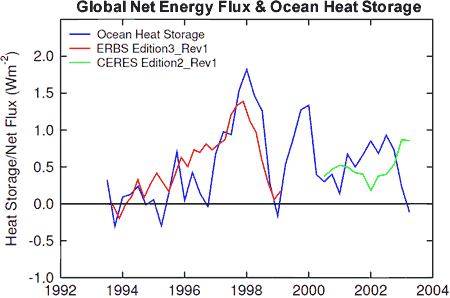
Figure 2: Global ocean heat storage (blue) against global net flux anomalies (Wong 2005).
The climate is not heading towards equilibrium. Rather, the radiative imbalance is increasing with the climate steadily receiving more energy than it is radiating back out into space. And this is where the true significance of climate time lag lies. Even if the radiative imbalance were to level off at its current rate of around 0.85W/m2, it would take several decades for the climate to return to radiative equilibrium. Based on this climate lag, Hansen 2005 calculates there is still 0.6°C warming still "in the pipeline".































 Arguments
Arguments























 0
0  0
0






Comments