
Figure 1: coefficients of determination (R2) values for subsequent and overlapping 40-year intervals, of regression of Holgate 2007 global mean sea level trend against sunspot count
In April 2009, climate change contrarian blog WattsUpWithThat? hosted a guest post from David Archibald entitled "Archibald on sea level rise and solar cycles" in which Archibald presented a graph he made showing a supposed causal correlation between solar output and global mean sea level (GMSL) trend data. Since then, in early February this year David Archibald expanded on his initial post, again on WUWT, and that new article can be viewed here.
What David Archibald is arguing is that solar output is modulating the rate of sea level change, seemingly singularly, and that sea level will drastically fall over the coming decades as we approach an implied Grand Solar Minimum. David Archibald tells in his post that he was apparently able to change the minds of the governing officials in New South Wales (Australia), who had been influenced by "evil environmentalists" to pass a regulation requiring issued building permits to be based on a projected ~1 meter sea level rise by the end of the twenty-first century. If David Archibald is correct about his projection, then great, we don't have to worry about sea level rise and New South Wales doesn't have to bother its councils about such a regulation.
Unfortunately, aside from a couple of superficially convincing graphics showing the overlay of the datasets, there is very little in the way of legitimate statistical analysis in David Archibald's post. Instead, what we are given is a very over-simplified model for sea level trend, cherry picked regressions, and a lack of consideration for the most important factor in drawing causality from correlation: chronology. In this set of posts, I will cover several of the basic statistical problems with David Archibald's analysis, and will discuss other factors that have influenced sea level variability during the twentieth century that David Archibald simply ignores.
First, where we're even getting our data: David Archibald does not make it terribly obvious from where he was deriving his GMSL trend data, though I did not have much difficulty finding it all the same. The GMSL trend data is from Holgate 2007, "On the decadal rates of sea level change during the twentieth century," published in GRL. The data is not avialable online from what I could (not) find, and wanting to recreate these graphics myself I contacted Dr. Simon Holgate, who was gracious enough to send me the data used in his paper and weigh in on the issue a bit as well. For comparing against solar output, both David Archibald and I use sunspot data, which I was able to download here.
The problems begin with Archibald's choice of time frame for comparing GMSL trend to solar output. He states:
"Using the period of best fit from 1948-1987, the relationship between solar activity and sea level is found to be 0.045 mm per unit of sunspot number."
A couple of issues here need to be addressed. First is his choice of that specific 40-year interval. What Archibald has done, by his own admission, is chosen the 40-year period that gives the best fit between the two datasets, and calculated the "relationship" based off of that. To illustrate, I have plotted the coefficients of determination (R2) for each 40-year period starting in 1909(-1948) through 1961-2000. Each coefficient is placed above its interval's start year.

Figure 1: coefficients of determination (R2) values for subsequent and overlapping 40-year intervals, of regression of Holgate 2007 global mean sea level trend against sunspot count
David Archibald's pick of 1948-1987 is given by the black dot. Our values differ very slightly (mine is 0.5438, his 0.5381), perhaps due to different sources of sunspot data, though this point remains: Archibald chose to quantify the "relationship" between solar output and sea level trend by choosing the interval over which they were best correlated, a time interval which ended over two decades ago. As one can see too, the correlation between the two datasets has drastically decreased, almost exclusively, since that peak. That would indicate that either solar output for some reason is now having a more marginalized impact on GMSL trend, or (and perhaps more likely) that the relationship between the two was spurious from the start.
Second: the choice of a 40-year interval is arbitrary and excludes over half a century of data in the "relationship" calculation. When we plot the two datasets against each other in full, while we can probably predict how this will turn out based on the previous figure, we can get a better sense of how strong the "relationship" really is.

Figure 2: regression of Holgate 2007 global mean sea level trend against sunspot count, 1909-2000
Note how we now have a much worse correlation, barely positive. If solar output is driving sea level trend, we would not expect such noise in the data, since solar output is predictably periodic. There certainly is noise though, caused by other factors that affect GMSL trend, factors that Archibald again did not consider. I will go into those in more detail later in Part 2.
David Archibald states:
"What is very interesting is that during four solar minima over the 20th Century, sea level fell during those minima. That means that during prolonged solar activity, sea level can be expected to continue falling."
We'll start here. I have recreated David Archibald's comparison figure below. The axes are slightly off due to scaling differences, but the overall effect is minimal and not important to this post.

Figure 3: Holgate 2007 global mean sea level trend, and sunspot sount, 1909-2000
There are 9 solar minima that occurred during the twentieth century. During 5 of these (instead of 4) as well, GMSL according to Holgate 2007 did indeed fall, if ever so slightly and briefly.
Even with the included fifth minimum during which sea level fell, that does not change the fact that 5/9 is simply not a high enough proportion to argue that sea level generally falls during a solar minimum. If a hypothesis cannot correctly predict reality half of the time, there are fundamental flaws in it. Assuming even that the solar link is so strong as Archibald suggests, choosing to only focus on those minima where sea level falls to make a general statement about GMSL response is sloppy and cherry picking.
There is also dissonance between Archibald's assertion that GMSL falls during "prolonged" low solar activity and the data. It is here that I'll shortly turn to total solar irradiance, instead of sunspots – reconstructions of twentieth century total solar irradiance, such as by Solanki and Krivova 2007 (below) or Krivova et al 2010, show that total solar irradiance was lower during the first half of the twentieth century than during the latter.
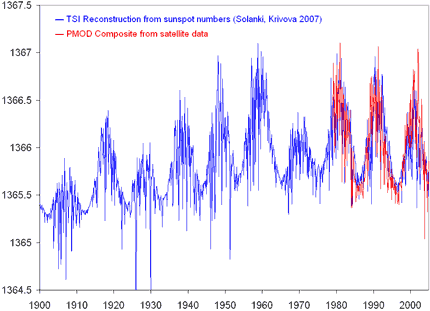
Figure 4: total solar irradiance reconstruction (blue), from Solanki and Krivova 2007, compared to PMOD composite (red)
Yet, 4 of the 5 brief periods of negative GMSL trend occurred during the latter half of the century when solar output (including the minima) was generally higher, as opposed to when solar output was lower in the first half. This calls into question whether or not it was actually solar output that pushed the sea level trend values slightly negative each time; or whether that was due to noise, or to other factors. We'll have a look at (at least) the latter in Part 2.
David Archibald continues later on, after calculating the "relationship":
"The threshold between rising and falling sea level is a sunspot amplitude of 40. Below 40, sea level falls. Above that, it rises."
But is that true? If we accept the linear fit as being perfect, this would be acceptable – but it's not perfect. It's the best fit to the data (despite being a rather poor fit), but the data simply don't agree with Archibald's threshold assertion. Using his own graphic first, and the 40-year period of best correlation, there are 7 data points where GMSL trend is actually negative while sunspots are at or below 40, but there are 8 points where GMSL trend is positive, quite strongly so in some cases. Again, half of the data disagrees with Archibald's "relationship." The mean sea level trend of all data points below 40 sunspots is +0.446 mm/year.
As said above though, focusing only on that time frame excludes over half a century of data. Let's look again at Figure 2, but this time I have plotted all of the points below the intercept as red markers.

Figure 5: regression of Holgate 2007 global mean sea level trend against sunspot count, 1909-2000; points falling below trend y-intercept marked in red
Below the linear model's intercept (45 sunspots), and where sea level supposedly falls, there are 13 observations where GMSL indeed falls. However, there are a total 29 points where the trend is positive, and the mean sea level trend for all the data points below the intercept is +1.32 mm/year.
This isn't to say that sea level will necessarily rise though if solar output is below that threshold, or even that it generally will. When we use all of the data, the correlation is rather poor between the sunspots and GMSL trend. We can almost always obtain an ordinary least squares fit through such poorly correlated data that will cross the y-axis at some point if we carry it out far enough. It's rather convenient that we have some negative sea level trend data so that we don't have to extrapolate outside our observational limit, but the massive bias of that data to being positive below our intercept tells us just how poor our linear model is at representing sea level trend. We thus need to be very cautious about the conclusions we draw when we extrapolate that trend in time to comment on behavior of potential future values at the fringe. David Archibald's argument is not at all convincing, mainly stemming from his issue of excluding over half of the data, which is a large issue in and of itself and an issue that, when corrected, disallows any conclusion of a robust "relationship."
The "relationship" falls apart at the inclusion of more data if we do a comparison of sunspots in a given year to GMSL trend in that same year. However, that's far from being the most dismissing argument against this connection between solar output and GMSL trend. If we (or Archibald) want to argue that it is solar output that modulates GMSL trend, then we should expect the best correlation between the two datasets when they are compared either concomitantly (i.e. at the same spot in time), or with sea level lagging solar changes due to perhaps thermal inertia of the oceans. The size of this lag is an important topic if we want to know how strong the solar signal is in the GMSL trend data, but if the chronology is reversed, then it is a secondary argument.
First, take a look again at Figure 3, and note the peaks (minima and maxima) and see how they match up. These can give us an idea of whether or not changes in solar output start before or after changes in GMSL trend. For all of the solar peaks, GMSL trend responds as below these many times:
| Leads by X years | 5 times |
| Lags by X years | 6 times |
| Changes same time | 5 times |
| No obvious correlation | 2 times |
That's a rather even spread. For convenience, I have highlighted such times in the below figures. The shading depth* and width of the bars (*except for the red bars indicating no obvious correlation, and the blue bars in Figure 7) indicate how long each lead/lag is.

Figure 6: Holgate 2007 and sunspots - concomitant peaks highlighted blue, periods of no or opposite correlation highlighted red

Figure 7: Holgate 2007 and sunspots - periods where sea leads solar output highlighted orange, periods of no or opposite correlation highlighted red

Figure 8: Holgate 2007 and sunspots - periods where sea lags solar output highlighted green, periods of no or opposite correlation highlighted red
The peaks only give us a general understanding of how the two behave relative to each other, but what they tell us is that the lead/lag relationship is quite unstable, and unphysical at several points. If solar output is the sole driver of sea level change, as Archibald implies by his solely solar projection and lack of discussion on other factors, then GMSL trend cannot change before solar output. This is simple causality. We should reject the singular solar causative model at this point.
This is also something that such a regression as plotting each on its own axis (i.e. Figure 1, or Figure 2) cannot tell us. We can still obtain some pretty good correlation (assuming we're choosy with what data we select for comparison) between datasets that slightly lead/lag each other, but the regression won't tell us anything about whether or not the result is physically feasible in nature. It helps to keep in mind the exact context of the problem we're looking at. If we use Archibald's method of picking the best-fitting 40-year period for comparison, then we can find that interval by using Figure 1 above. To better show just how concerning this causality problem is though, I repeated the process that produced Figure 1; however, I have lagged solar outut by a year in the correlation calculations, and have compared that to our original. I've also included a time series of the correlations when GMSL trend lags by a year.

Figure 9: coefficients of determination (R2) values for subsequent and overlapping 40-year intervals, of regression of Holgate 2007 global mean sea level trend against sunspot count; concomitant data in blue, 1-year solar lag in red, 1-year sea lag in green
This is an important outcome. Not only do we have a considerably higher peak in correlation when solar output lags by a year (including a higher correlation at the time interval Archibald chose), but the "solar-lag" scenario has better correlation for almost all of the 40-year intervals from the start of the record to the 1948-1987 interval. The steep drop-off is because (and let's look back to Figure 8 to see) solar output begins to lead sea level trend, and rather considerably too. The "sea-lag" scenario actually obtains higher correlation than the other two during the last three of the 40-year intervals. The sea level lag itself is perhaps physically reasonable (certainly when contrasted to a solar lag), but that still leaves the question of why such a change in lead/lag pattern came about in the first place. That needs a physical explanation, and considering all of what we have covered so far, perhaps the simplest is that the "relationship" between solar output and GMSL trend is specious at best.
Yes. There's the fact that it did not consider any other factors that we know have impacted sea level over the past century, and factors that we know will impact sea level in the coming century. We also have one more problem that I have not mentioned until this point: issues with Holgate 2007 itself, or perhaps more appropriately the fact that we're even using data from it. The intent of Holgate 2007 was to see if high quality, very long term tidal gauges (of which there are only a few) could be reliable measures of GMSL trend, as reliable as much larger reconstructions from hundreds of tidal gauges. Only 9 gauges were used in Holgate 2007, and it is not clear at all that so few should be used when trying to identify such signals in GMSL trend data. Holgate 2007 did conclude that for the purposes of that study, the few tidal gauges were adequate:
"The use of a reduced number of high quality sea level records was found to be as suitable in this type of analysis as using a larger number of regionally averaged gauges."
but issues of increased variability due to low gauge count and some dissonance compared to other, more comprehensive global reconstructions should be indicators that we would want to at the very least look at other sea level datasets besides just this one. We can then see if such a solar/sea relationship exists. In Part 2, I will cover all of these issues – other factors that impact global sea level, and some analysis with comprehensive global sea level datasets.
This Part 1 is also somewhat simplistic in its approach to the issue. There are more formal and more robust ways of approaching the topic of frequency correlation between two series, and probably some unintended effects on our analysis due to the current choice of trend processing (as implemented in Holgate 2007), and I will be sharing the results of such tests in Part 2 and providing discussion on what they mean. At the time of writing this I have yet to perform these tests, so it will be something to look forward to for everyone (and if it is necessary, I will reconsider my position and conclusion). I'll also cover some more miscellaneous and minor issues with Archibald's post (such as choice of local station data for comparing for New South Wales, and so on). Stay tuned.
Posted by Alex C on Wednesday, 4 April, 2012
 |
The Skeptical Science website by Skeptical Science is licensed under a Creative Commons Attribution 3.0 Unported License. |