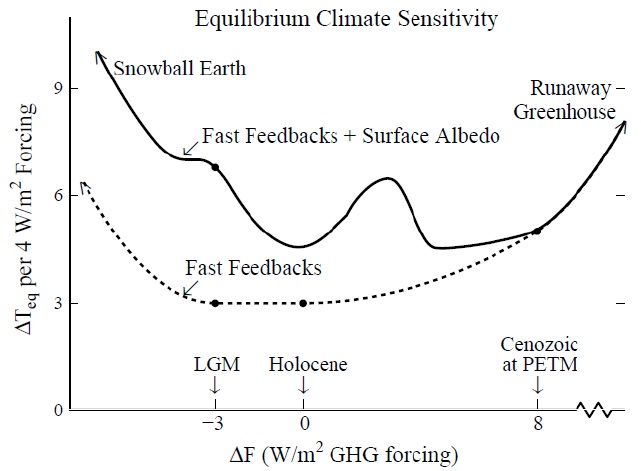
James Hansen and Makiko Sato from the NASA Goddard Institute for Space Studies (GISS) have made available a new draft paper, Climate Sensitivity from Earth's History (HS12). The paper discusses reconstructions of global deep ocean temperature, sea level, surface temperature, and climate sensitivity going back thousands to millions of years. HS12 is similar to a previous study, Hansen and Sato (2011) (HS11), but incorporates some updated data (e.g. revised radiative forcing estimates). Here we will mainly focus on the surface temperature and climate sensitivity analysis in HS12 and its implications for the future of our climate. We will see that HS12 provides an empirically-based climate sensitivity estimate which is consistent with estimates from today's climate models. Figure 7 from HS12, our Figure 1 below, summarizes the authors' climate sensitivity conclusions.
Figure 1: Schematic diagram of the equilibrium fast-feedback climate sensitivity and Earth system sensitivity that includes surface albedo slow feedbacks. Figure 7 from HS12.
In order to understand Figure 1, let's delve into some of the details of the paper.
HS12 uses the oxygen isotope record in ocean sediments Zachos et al. (2008) to estimate past changes of sea level and ocean temperature, and thus obtain a largely empirical estimate of climate sensitivity. HS11 (which is currently in press, and will actually be published in 2012) had used a previous version of that data set, publshed in 2001. The Zachos 2008 data are shown in HS12 Figure 1, our Figure 2 below.
Figure 2: (a) Global deep ocean δ18O from Zachos et al. (2008) and (b) deep ocean temperature, with the latter based on the prescription in HS12. Black data points are 5-point running means of original temporal resolution; red and blue curves have 500 ky resolution. Figure 1 from HS12.
Deep ocean temperature is approximated as linearly proportional to the fraction of the heavy oxygen istotope (δ18O), though Hansen has concluded that the proportion depends on the size of the continental ice sheets. As Earth became colder and continental ice sheets grew, further increase of δ18O was due in equal parts to deep ocean temperature change and ice mass change.
HS12 notes that as we are surface dwellers, the surface air temperature is of most interest to humans. HS12 assume that deep ocean temperature change was similar to global mean surface temperature change for Cenozoic climates warmer than today, but this relationship does not hold true for colder climates.
"deep ocean temperature change does not provide a good indication of surface temperature change when the deep ocean approaches the freezing point, as quantified by Waelbroeck et al. (2002). The empirical data show that deep ocean cooling slows relative to global mean surface cooling as the area of ice and snow on the surface expands, consistent with the fact that the increase of δ18O between the Holocene and LGM was due more to ice sheet growth than to deep ocean cooling."
The Last Glacial Maximum (LGM) approximately 20,000 years ago is a period often used to estimate climate sensitivity, because it represents a large climate shift in the relatively recent past, of which we have reasonably good measurements.
There have been a number of estimates of the average global surface temperature change during the LGM. Most studies estimate the change close to 5°C, although there are some outliers, such as a paper we previously examined and which garnered a great deal of attention and misrepresentation from climate contrarians, Schmittner et al. (2011). Schmittner et al. estimated the LGM cooling at only approximately 3°C, although as we discussed, this estimate was based heavily on sea surface temperature (SST) reconstructions from Multiproxy Approach for the Reconstruction of the Glacial Ocean (MARGO) project, which may underestimate the SST change. This relatively low glacial-interglacial temperature change estimate contributed to the relatively low climate sensitivity estimate of Schmittner et al. (more on this below).
HS12 discusses another paper on the subject, Schneider von Deimling et al. (2006), which used an intermediate complexity climate model to estimate an LGM cooling of 5.8 ± 1.4°C, which is about twice as large as Schmittner et al., who fed their primarily MARGO-based temperatures into a climate model to estimate climate sensitivity.
Another paper we recently discussed, Shakun et al. (2012), estimated the global surface temperature change in the LGM cooling at 4.9°C. HS12 reviews a number of other temperature estimates, including from the Vostok Antarctic ice core, and arrives at its LGM cooling estimate.
"Our estimate of LGM global cooling is thus 4.5±0.5°C, where 0.5°C is our estimated one standard deviation (σ) uncertainty. This range is meant to imply that there is about a 68% chance that the LGM global cooling was in the range 4-5°C, and about a 95% change that the cooling was in the range 3.5-5.5°C."
HS12 comments on the value of model-based results such as in the Schneider von Deimling and Schmittner studies.
"These model-based studies provide invaluable insight into the functioning of the climate system, because it is possible to vary processes and parameters independently, thus examining the role and importance of different climate mechanisms. However, the model studies also make clear that the results vary substantially from one model to another, and experience of the past few decades suggests that models are not likely to converge to a narrow range in the near future.
Therefore there is considerable merit in also pursuing a complementary approach that estimates climate sensitivity empirically from known climate change and climate forcings."
This empirically-based approach is the one Hansen and Sato pursue in this paper, while noting of course that their approach cannot be wholly independent of climate modeling, for example relying on radiative forcing computations from climate models, which is the most accurate way to estimate the magnitude of various forcings. However, Hansen and Sato use climate models in a way that their climate sensitivity does not significantly influence their radiative forcing or the global temperature estimates that they use in this study.
"For example, the best global atmospheric models driven by specified sea surface temperatures can do a good job of simulating global temperature, winds and water vapor distributions. Thus such models can be used to help define the distribution of radiative constituents needed to calculate accurately the global climate forcing for alternative specifications of long-lived GHGs and surface albedo. Similarly, such global models can be used to help define global surface temperature for specified atmospheric composition and surface properties such as sea surface temperature."
In this manner, Hansen and Sato use climate models to help them estimate past radiative forcings and surface temperature changes using paleoclimate data without influencing their climate sensitivity estimates. Thus their result in a predominantly empirical one.
One challenge in examining past climate data is in determining what should be treated as a forcing (driving a climate change) and what should be considered a feedback (amplifying or dampening a climate change). Climate sensitivity is estimated by dividing the surface temperature change (which is influenced by both forcings and feedbacks) by the total radiative forcing (which does not include feedbacks). Thus considering more temperature influences as forcings will increase the denominator, leading to smaller past climate sensitivity estimates, and vice-versa.
Aerosols are a challenge in this regard. HS11 discussed that it would be best to treat natural aerosol emissions as a fast feedback rather than a forcing.
"There is nothing inherently wrong with defining aerosol changes to be a forcing, but it is practically impossible to accurately determine the aerosol forcing because it depends sensitively on the geographical and altitude distribution of aerosols, aerosol absorption, and aerosol cloud effects for each of several aerosol compositions. Moreover, aerosols adjust rapidly to a changing climate, so it is logical to include natural aerosol changes in the category of fast feedbacks.
The low estimates of climate sensitivity by Chylek and Lohmann (2008) and Schmittner et al. (2011), ~2°C for doubled CO2, are due in part to their inclusion of natural aerosol change as a climate forcing rather than as a fast feedback (as well as the small LGM-Holocene temperature change employed by Schmittner et al., 2011)."
Non-CO2 greenhouse gases (GHGs) could also be treated as either feedbacks or forcings. In their estimate, Hansen and Sato only consider GHGs (including non-CO2 GHGs) and surface albedo (reflectivity) as forcings.
"Our estimated LGM-Holocene forcings with 1σ uncertainties are 3±0.3 W/m2 for GHGs (range 2.4-3.6 W/m2 for 95% confidence) and 3±0.7 W/m2 for surface albedo (range 1.6-4.4 W/m2 for 95% confidence)."
Hansen and Sato also differentiate between fast feedback and longer-term climate sensitivity, as illustrated in Figure 1 above. Ice sheets can take centuries to millennia to melt or form, whereas sea ice changes occur much more rapidly (as we're currently seeing in the Arctic). Therefore, albedo changes associated with sea ice are included in the fast feedback climate sensitivity, whereas albedo changes associated with ice sheets are only included in longer-term climate sensitivity estimates (which is termed "Earth System Sensitivity").
Thus given a total radiative forcing between the LGM and Holocene of approximately 6 W/m2, and a surface temperature change of approximately 4.5°C, HS12 arrives at a climate sensitivity best estimate of 3±0.5°C for a 4 W/m2 forcing (which is approximately equivalent to a doubling of atmospheric CO2). While this value is consistent with today's model-based estimates, Hansen and Sato note,
"the empirical paleoclimate estimate of climate sensitivity is inherently more accurate than model-based estimates because of the difficulty of simulating cloud changes (NYTimes, 2012), aerosol changes, and aerosol effects on clouds."
The NYTimes reference in this quote is to the piece by Justin Gillis which we previously examined. While climate contrarians like Richard Lindzen tend to treat the uncertainties associated with clouds and aerosols incorrectly, as we noted in that post, they are correct that these uncertainties preclude a precise estimate of climate sensitivity based solely on recent temperature changes and model simulations of those changes.
However, as Hansen notes, empirical estimates of climate sensitivity based on paleoclimate data are consistent with the sensitivity in climate models of approximately 3°C for doubled atmospheric CO2. In fact, as Figure 3 shows, the fit to the temperature data when multiplying the estimated radiative forcing by a climate sensitivity of 3°C for doubled CO2 is remarkably good.
Figure 3: Black curve: calculated surface air temperature change for climate forcings in HS12 and climate sensitivity 0.75°C per W/m2. Red curve: estimated global surface air temperature change based on deep ocean temperatures and assumption that LGM-Holocene surface temperature change is 4.5°C. Zero point is the 800 ky mean. Figure 6 from HS12.
Hansen and Sato examine the longer-term Earth System Sensitivity by adding in slow feedbacks one-by-one, starting with surface albedo. Hansen and Sato note the longer-term sensitivity is
"...more dependent on the initial climate state and the sign of the forcing. The fast-feedback climate sensitivity is a reasonably smooth curve, because the principal fast-feedback mechanisms (water vapor, clouds, aerosols, sea ice) do not have sharp threshold changes. Minor exceptions, such as the fact that Arctic sea ice may disappear with a relatively small increase of climate forcing above the Holocene level, might put a small wave in the fast-feedback curve."
This initial state dependency is illustrated by the more complex shape of the upper curve in Figure 1 above. For example, during a cooling event to a glacial period like the LGM, the long-term Earth System Sensitivity is approximately 6°C for an equivalent forcing to a doubling (or in this case halving) of CO2. This is primarily due to the increase in the Earth's reflectivity as large ice sheets form.
During a period like the Holocene while warming to a Pliocene-like climate, slow feedbacks (such as reduced ice and increased vegetation cover) increase the sensitivity to around 4.5°C for doubled CO2. However, a climate warm enough to lose the entire Antarctic ice sheet would have a long-term sensitivity of close to 6°C. Fortunately it would take a very long time to lose the entire Antarctic ice sheet.
Note also that the Earth System Sensitivity is deduced from various past climate change events like the Paleocene–Eocene Thermal Maximum (PETM), but the qualitative estimates of longer-term climate sensitivity are less precise than the HS12 fast feedback sensitivity estimates. Hence the authors note that Figure 1 above is a schematic.
Hansen and Sato argue that the probable range of climate sensitivity values is not as large as currently believed (unlikely to fall outside the range of 2 to 4°C for doubled CO2) - both very high and very low values can effectively be ruled out using paleoclimate data. This is also a position advocated by James Annan using a statistical approach, for example. Climate contrarians often argue that model-based climate sensitivity estimates are unreliable and empirical estimates suggest that climate sensitivity is low. On the contrary, HS12 shows that empirical estimates are consistent with climate models (as has also been previously shown by Knutti and Hegerl, for example [Figure 4]).
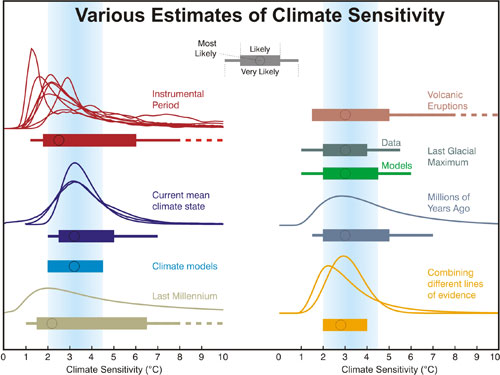
Figure 4: Distributions and ranges for climate sensitivity from different lines of evidence. The circle indicates the most likely value. The thin colored bars indicate very likely value (more than 90% probability). The thicker colored bars indicate likely values (more than 66% probability). Dashed lines indicate no robust constraint on an upper bound. The IPCC likely range (2 to 4.5°C) and most likely value (3°C) are indicated by the vertical grey bar and black line, respectively. Adapted from Knutti and Hegerl (2008).
In short, all lines of evidence point to a climate sensitivity of close to 3°C for doubled CO2, which in turn points to a very dangerous amount of global warming if we continue on a business-as-usual path.
Posted by dana1981 on Thursday, 24 May, 2012
 |
The Skeptical Science website by Skeptical Science is licensed under a Creative Commons Attribution 3.0 Unported License. |