Are we too stupid?
Guest post by Jacob Bock Axelson
In a recent interview, the famous environmentalist James Lovelock bluntly stated that “humans are too stupid” to mitigate global warming. Perhaps a better question is whether or not there is any way that we can cooperate in preventing climate change. This subject has been part of the research performed by the evolutionary biologist Manfred Milinski and co-workers at the Max Planck Institute in Plön, Germany. The Milinski group have identified that indirect reciprocity, information and perceived risk are important pieces of the puzzle. To better understand these concepts, and the results, we will briefly review the game theory of cooperation. Before we begin I should mention that cooperativity may have very strong switch-like dynamics e.g. whereas an agency with thousands of workers and engineering PhDs can produce low risk manned lunar flights, infinite individual geniuses cannot. Therefore, evolution has favoured cooperativity in biophysical mechanisms such as membrane formation, enzyme kinetics, protein folding, genetic regulation, cellular interaction and flock behavior.
In 1968 Garrett Hardin addressed the issue of misuse of common goods in the famous paper entitled "The Tragedy of the Commons". The paper created enormous controversy and has thus been cited more than 3608 times in the scientific literature (according to ISI Web of Knowledge). Hardin’s idea was based on the premise that the cost of individual use of common goods is distributed to the community. Individuals may then act according to their misguided self-interest and utilize any common resource to depletion – an individually undesirable state. Hardin mentions that psychological denial is evolutionary favorable and states: "The individual benefits (...) from his ability to deny the truth even though society as a whole, of which he is a part, suffers." Thus, one may regard the tragedy-of-the-commons partly as a consequence of individual illusory superiority (also known as the Dunning-Kruger effect). As it were, the ancient greeks had already identified some problems of unlimited freedom, in 1624 the poet John Donne wrote the famous phrase "no man is an island, entire of itself" and in 1882 the playwright Henrik Ibsen wrote the play "An Enemy of the People" on the problems of dealing with pollution. More interestingly, many native peoples are known to have somewhat successfully managed common resources such as the active use of wildfires by native Americans.
In 1971 Robert Trivers coined the term "reciprocal altruism" or "you scratch my back, I scratch yours" as a short description of the mechanism of rewarding someone for their good deeds (Trivers 1971). Major progess was seen when Axelrod and Hamilton let academics write strategies for computer tournaments and subsequently published the results in the famous paper "The Evolution of Cooperation" in 1981. The question was: what is the optimal strategy when a group of generally unrelated individuals play the Prisoner’s Dilemma (see figure below) over and over again?
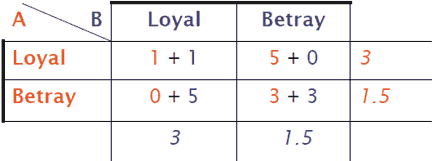
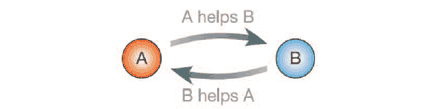
Figure 1: Top: Prisoner’s dilemma punishment matrix (years in prison per game). ‘Loyal’ means that you do not reveal information about your friend and ‘Betray’ means that you help the police. The colors and sums shows the consequences of the player’s choices. By minimizing the personal average punishment (in italics) the game thus reaches the stable Nash equilibrium of snitching. Contrary to this, the unstable Pareto optimum is that both are loyal because at least one prisoner will be unhappy with exchanging their 1-year sentence with 5 or 3. Bottom: the tit-for-tat (direct reciprocity) strategy.
The superior, strikingly simple, strategy was conceived by the mathematical psychologist Anatol Rapoport, whom had worked on the Prisoner's Dilemma for years. The strategy was that you should initially cooperate and then reciprocate your opponent i.e. start by being nice and then do what your opponent did to you last time - also known as direct reciprocity. The strategy was termed "tit-for-tat", which in the nuclear arms race had an extreme cousin known as "mutual assured destruction" and it bore resemblance to the legal concept "eye-for-an-eye" found in the Torah.
The result seemed to explain the emergence of cooperation if it were not for the fact that the dynamics in this simplified setup is highly unstable and prone to enter a "tragedy of the commons"-like scenario. Say a single one-time misunderstanding occurs: you misunderstand and think you have been cheated so you will cheat in the next round thus spurring more cheating of your partner. The “tit-for-two-tats” strategy proposed by Axelrod partly solved this instability problem. Many other strategies have been proposed amongst which the “win-stay lose-shift” (or Pavlov) strategy by Nowak and Sigmund (1993) performed markedly better in the long run than various tit-for-tat strategies. Put simply, by acting ‘as per reflex’ you could avoid sharp retaliations caused by misunderstandings.
The next major contribution was again made by Nowak and Sigmund (1998) when they studied the aspects of indirect reciprocation in evolutionary learning games. The game is the same as the Prisoner’s dilemma, but some players may now choose to punish, or discriminate against, the defectors. The inclusion of such indirect reciprocity inevitably complicates the understanding of the dynamics (see figure 2 and 3 below).
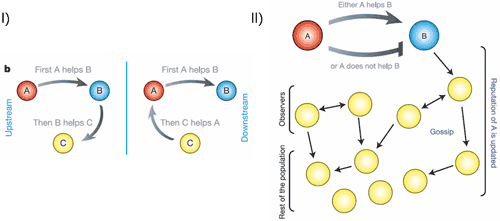
Figure 2: I) Indirect reciprocity. II) Building a reputation in the population affecting your future. Nowak and Sigmund (2005)
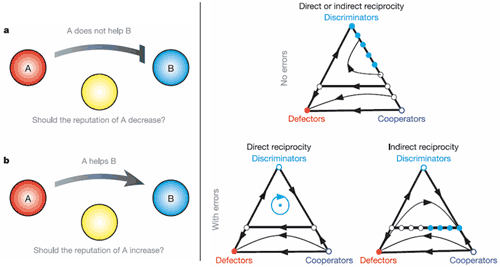
Figure 3: (left) Problems with indirect reciprocity. B has recently not helped anyone i.e. defected for some time. Should C altruistically sacrifice reputation by not helping A if A logically does not help the defector B? (right) The dynamics of a simplified game of “the good, the bad and the discriminator”. The triangle is a phase portrait i.e. the time evolution of the ratios of each type of player. Note that without sufficient discriminators/punishers everybody ends up defecting (the red lower left corner is the final outcome for the lower part of the combinations of player types). Nowak and Sigmund (2005)
All of the above is purely theoretical and somewhat confusing. Therefore there has recently been a strong interest in performing experiments with real test subjects. In 2005 Milinski and co-workers let students play a new kind of common goods game where funds are pooled to invest in mitigating climate change (Milinski 2005). They found that a finite - probably insufficient - level of altruism was always present in a population. If players were also enlightened with expert knowledge on the climate they even cooperated significantly more. Furthermore, allowing participants to take reputation into account and use indirect reciprocity also lead to cooperation comparable to publicly displaying the players’ level of altruism.
In 2008 the Milinski group found that only if disaster was 90% certain, i.e. the individual would suffer irreversible losses, could humans be motivated to reach a given target of total required preventive investments (Milinski 2008).
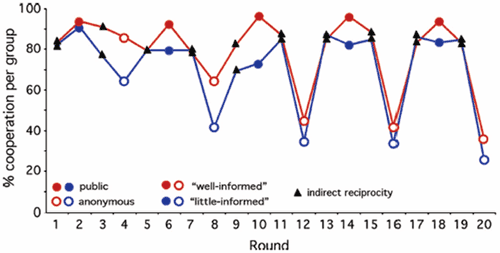
Figure 4: Results of the climate change game with real humans. Students were initially given an amount and in subsequent rounds asked to invest in a common climate pool. Filled circles were when investments were done publicly and open circles for when the investments were anonymous. The triangles was rounds when players was allowed to see each other’s investment history and decide to help each other. Red is for enlightened participants and blue for unenlightened. Blue open circles then gives a (slowly decreasing) basic level of altruism. Milinski et al. (2005).
In conclusion, theory and experiment indicates that we may be able to cooperate on climate change if a) social punishment is strong and active and b) the population is sufficiently enlightened about the facts and c) everybody knows that they will pay a price if they do not contribute in time. Lovelock probably knows this and simply finds the demands too high. In any case, the minimum 10-20 years it could take to replace the use of fossil carbon is the time it will take to reveal most of the final answer.
Posted by Jacob Bock Axelsen on Tuesday, 6 April, 2010






