
Let’s face it. The claim of uncertainty is a common argument against taking action on any prediction of future harm. “How do you know, for sure?”. “That might not happen.” “It’s possible that it will be harmless”, etc. It takes on many forms, and it can be hard to argue against. Usually, it takes a lot more time, space, and effort to debunk the claims than it takes to make them in the first place.
It even has a technical term: FUD.
Acronym of Fear, uncertainty, and doubt, a marketing strategy involving the spread of worrisome information or rumors about a product.
During the times when the tobacco industry was discounting the risks of smoking and cancer, the phrase “doubt is our product” was purportedly part of their strategy. And within the climate change discussions, certain individuals have literally made careers out of waving “the uncertainty monster”. It has been used to argue that models are unreliable. It has been used to argue that measurements of global temperature, sea ice, etc. are unreliable. As long as you can spread enough doubt about the scientific results in the right places, you can delay action on climate concerns.

Figure 1: Is the Uncertainty Monster threatening the validity of your scientific conclusions? Not if you've done a proper uncertainty analysis. Knowing the correct methods to deal with propagation of uncertainty will tame that monster! Illustration by jg.
At lot of this happens in the blogosphere, or in think tank reports, or lobbying efforts. Sometimes, it creeps into the scientific literature. Proper analysis of uncertainty is done as a part of any scientific endeavour, but sometimes people with a contrarian agenda manage to fool themselves with a poorly-thought-out or misapplied “uncertainty analysis” that can look “sciencey”, but is full of mistakes.
Any good scientist considers the reliability of the data they are using before drawing conclusions – especially when those conclusions appear to contradict the existing science. You do need to be wary of confirmation bias, though – the natural tendency to accept conclusions you like. Global temperature trends are analyzed by several international groups, and the data sets they produce are very similar. The scientists involved consider uncertainty, and are confident in their results. You can examine these data sets with Skeptical Science’s Trend Calculator.
So, when someone is concerned about these global temperature data sets, what is to be done? Physicist Richard Muller was skeptical, so starting in 2010 he led a study to independently assess the available data. In the end, the Berkeley Earth Surface Temperature (BEST) record they produced confirmed that analyses by previous groups had largely things right. A peer-reviewed paper describing the BEST analysis is available here. At their web site, you can download the BEST results, including their uncertainty estimates. BEST took a serious look at uncertainty - in the paper linked above, the word “uncertainty” (or “uncertainties”) appears 73 times!
The following figure shows the BEST values downloaded a few months ago, covering from 1850 to late 2022. The uncertainties are noticeably larger in the 1800s, when instrumentation and spatial coverage are much more limited, but the overall trends in global temperature are easily seen and far exceed the uncertainties. For recent years, the BEST uncertainty values are typically less than 0.05°C for monthly or annual anomalies. Uncertainty does not look like a worrisome issue. Muller took a lot of flak for arguing that the BEST project was needed – but he and his team deserve a certain amount of credit for doing things well and admitting that previous groups had also done things well. He was skeptical, he did an analysis, and he changed his mind based on the results. Science as science should be done.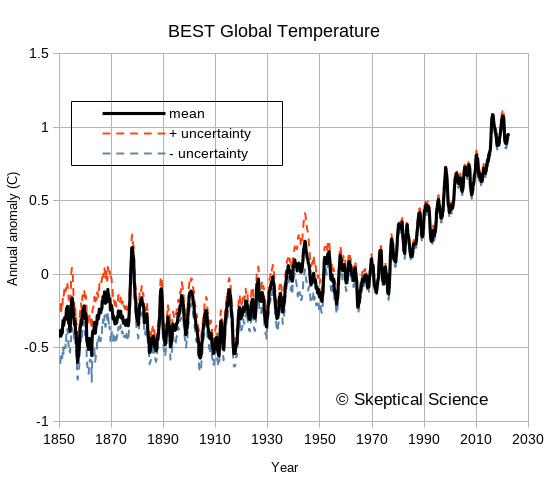
Figure 2: The Berkeley Earth Surface Temperature (BEST) data, including uncertainties. This is typical of the uncertainty estimates by various groups examining global temperature trends.
So, when a new paper comes along that claims that the entire climate science community has been doing it all wrong, and claims that the uncertainty in global temperature records is so large that “the 20th century surface air-temperature anomaly... does not convey any knowledge of rate or magnitude of change in the thermal state of the troposphere”, you can bet two things:
We’re here today to look at a recent example of such a paper: one that claims that the global temperature measurements that show rapid recent warming have so much uncertainty in them as to be completely useless. The paper is written by an individual named Patrick Frank, and appeared recently in a journal named Sensors. The title is “LiG Metrology, Correlated Error, and the Integrity of the Global Surface Air-Temperature Record”. (LiG is an acronym for “liquid in glass” – your basic old-style thermometer.)
Sensors 2023, 23(13), 5976
https://doi.org/10.3390/s23135976
Patrick Frank has beaten the uncertainty drum previously. In 2019 he published a couple of versions of a similar paper. (Note: I have not read either of the earlier papers.) Apparently, he had been trying to get something published for many years, and had been rejected by 13 different journals. I won't link to either of these earlier papers here,, but a few blog posts exist that point out the many serious errors in his analysis – often posted long before those earlier papers were published. If you start at this post from And Then There’s Physics, titled “Propagation of Nonsense”, you can find a chain to several earlier posts that describe the numerous errors in Patrick Frank’s earlier work.
Today, we’re only going to look at his most recent paper, though. But before we begin that, let’s review a few basics about the propagation of uncertainty – how uncertainty in measurements needs to be examined to see how it affects calculations based on those measurements. It will be boring and tedious, since we’ll have more equations than pictures, but we need to do this to see the elementary errors that Patrick Frank makes. If all the following section looks familiar, just jump to the next section where we point out the problems in Patrick Frank’s paper.
Spoiler alert: Patrick Frank can’t do basic first-year statistics.
Every scientist knows that every measurement has error in it. Error is the difference between the measurement that was made, and the true value of what we wanted to measure. So how do we know what the error is? Well, we can’t – because when we try to measure the true value, our measurement has errors! That does not mean that we cannot assess a range over which we think the true measurement lies, though, and there are standard ways of approaching this. So much of a “standard” that the ISO produces a guide: Guide to the expression of uncertainty in measurement. People familiar with it usually just refer to it as “the GUM”.
The GUM is a large document, though. For simple cases we often learn a lot of the basics in introductory science, physics, or statistics classes. Repeated measures can help us to see the spread associated with a measurement system. We are familiar with reporting measurements along with an uncertainty, such as 18.4°C, ±0.8°C. We probably also learn that random errors often fit a “normal curve”, and that the spread can be calculated using the standard deviation (usually indicated by the symbol σ). We also learn that “one sigma” covers about 68% of the spread, and “two sigmas” is about 95%. (When you see numbers such as 18.4°C, ±0.8°C, you do need to know if they are reporting one or two standard deviations.)
At a slightly more advanced level, we’ll start to learn about systematic errors, rather than random ones. And we usually want to know if the data actually are normally-distributed. (You can calculate a standard deviation on any data set, even one as small as two values!, but the 68% and 95% rules only work for normally-distributed data.) There are lots of other common distributions out there in the physical sciences - uniform Poisson, etc. - and you need to use the correct error analysis for each type.
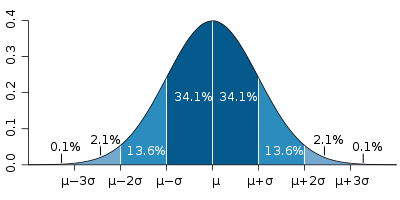
Figure 3: the "normal distribution", and the probabilities that data will fall within one, two, or three standard deviations of the mean. Image source: Wikipedia.
But let’s first look at what we probably all recognize – the characteristics of random, normally-distributed variation. What common statistics do we have to describe such data?
A key thing to remember is that measures such as standard deviation involve squaring something, summing, and then taking the square root. If we do not take the square root, then we have something called the variance. This is another perfectly acceptable and commonly-used measure of the spread around the mean value – but when combining and comparing the spread, you really need to make sure whether the formula you are using is applied to a standard deviation or a variance.
The pattern of “square things, sum them, take the square root” is very common in a variety of statistical measures. “Sum of squares” in regression should be familiar to us all.
Now, all that was dealing with the spread of a single repeated measurement of the same thing. What if we want to compare two different measurement systems? Are they giving the same result? Or do they differ? Can we do something similar to the standard deviation to indicate the spread of the differences? Yes, we can.
Although this looks very much like the standard deviation calculation, there is one extremely important difference. For the standard deviation, we subtracted the mean from each reading – and the mean is a single value, used for every measurement. In the RMSE calculation, we are calculating the difference between system 1 and system 2. What happens if those two systems do not result in the same mean value? That systematic difference in the mean value will be part of the RMSE.
Lastly, we’ll talk about how uncertainty gets propagated when we start to do calculations on values. There are standard rules for a wide variety of common mathematical calculations. The main calculations we’ll look at are addition, subtraction, and multiplication/division. Wikipedia has a good page on propagation of uncertainty, so we’ll borrow from them. Half way down the page, they have a table of Example Formulae, and we’ll look at the first three rows. We’ll consider variance again – remember it is just the square of the standard deviation. A and B are the measurements, and a and b are multipliers (constants).
| Calculation | Combination of the variance |
| f = aA | σf2 = a2 σ2A |
| f=aA+bB | σf2 = a2 σ2A + b2 σ2B + 2ab σAB |
| f=aA-bB | σf2 = a2 σ2A + b2 σ2B - 2ab σAB |
If we leave a and b as 1, this gets simpler. The first case tells us that if we multiply a measurement by something, we also need to multiply the uncertainty by the same ratio. The second and third cases tell us that when we add or subtract, the sum or difference will contain errors from both sources. (Note that the third case is just the second case with negative b.) We may remember this sort of things from school, when we were taught this formula for determining the error when we added two numbers with uncertainty:
σf2 = σ2A + σ2B
But Wikipedia has an extra term: ±2ab σAB, (or ±2σAB when we have a=b=1). What on earth is that?
Let’s finish with a simple example – a person walking. We’ll start with a simple claim:
“The average length of an adult person’s stride is 1 m, with a standard deviation of 0.3 m.”
There are actually two ways we can interpret this.
The claim is not actually expressed clearly, since we can interpret it more than one way. We may actually mean both at the same time! Does it matter? Yes. Let’s look at three different people:
Figure 4 gives us two random walks of the distance travelled over 200 steps by these three people. (Because of the randomness, a different random sequence will generate a slightly different graph.)
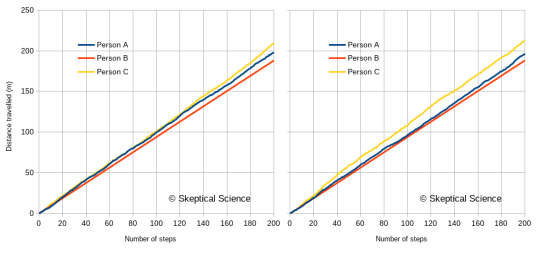
Figure 4: Two versions of a random walk by the three people described in the text. Person A has a stride of 1.0±0.3 m. Person B has a stride of 0.94±0.01 m. Person C has a stride of 1.06±0.3 m.
What’s the point? Well, to properly understand what the graph tells us about the walking habits of these three people, we need to recognize that there are two sources of differences:
Just looking at how individual steps vary across the three individuals is not enough. The differences have an average component (e.g., Mean Bias Error), and a random component (e.g., standard deviation). Unless the statistical analysis is done correctly, you will mislead yourself about the differences in how these three people walk.
Here endeth the basic statistics lesson. This gives us enough tools to understand what Patrick Frank has done wrong. Horribly, horribly wrong.
Well, just a few of them. Enough of them to realize that the paper’s conclusions are worthless.
The first 26 pages of this long paper look at various error estimates from the literature. Frank spends a lot of time talking about the characteristics of glass (as a material) and LiG thermometers, and he spends a lot of time looking at studies that compare different radiation shields or ventilation systems, or siting factors. He spends a lot of time talking about systemic versus random errors, and how assumptions about randomness are wrong. (Nobody actually makes this assumption, but that does not stop Patrick Frank from making the accusation.) All in preparation for his own calculations of uncertainty. All of these aspects of radiation shields, ventilation etc. are known by climate scientists – and the fact that Frank found literature on the subject demonstrates that.
One key aspect – a question, more than anything else. Frank’s paper uses the symbol σ (normally “standard deviation”) throughout, but he keeps using the phrase RMS error in the text. I did not try to track down the many papers he references, but there is a good possibility that Frank has confused standard deviation and RMSE. They look similar in calculations, but as pointed out above, they are not the same. If all the differences he is quoting from other sources are RMSE (which would be typical for comparing two measurement systems), then they all include the MBE in them (unless it happens to be zero). It is an error to treat them as if they are standard deviation. I suspect that Frank does not know the difference – but that is a side issue compared to the major elementary statistics errors in the paper.
It’s on page 27 that we begin to see clear evidence that he simply does not know what he is doing. In his equation 4, he combines the uncertainty for measurements of daily maximum and minimum temperature (Tmax and Tmin) to get an uncertainty for the daily average:
![]()
Figure 5: Patrick Frank's equation 4.
At first glance, this all seems reasonable. The 1.96 multiplier would be to take a one-sigma standard deviation and extend it to the almost-two-sigma 95% confidence limit (although calling it 2σ seems a bit sloppy). But wait. Checking that calculation, there is something wrong with equation 4. In order get his result of ±0.382°C, the equation in the middle tells me to do the following:
What Frank actually seems to have done is:
See how steps B and C are reversed? Frank did the division by 2 outside the square root, not inside as the equation is written. Is the calculation correct, or is the equation correct? Let’s look back at the Wikipedia equation for uncertainty propagation, when we are adding two terms (dropping the covariance term):
σf2 = a2 σ2A + b2 σ2B
To make Frank’s version – as the equation is written - easier to compare, let’s drop the 1.96 multiplier, do a little reformatting, and square both sides:
σ2 = ½ (0.3662)+ ½(0.1352)
The formula for an average is (A+B)/2, or ½ A + ½ B. In Wikipedia’s format, the multipliers a and b are both ½. That means that when propagating the error, you need to use ½ squared, = ¼.
So, sloppy writing, but are the rest of his calculations correct? No.
Look carefully at Frank's equation 5.

Figure 6: Patrick Frank's equation 5.
Equation 5 supposedly propagates a daily uncertainty into a monthly uncertainty, using an average month length of 30.417. It is very similar in format to his equation 4.
And equation 6 repeats the same error in propagating the uncertainty of monthly means to annual ones. Once again, the denominator should be 122, not 12. Another factor of 3.464.
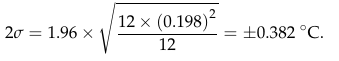
Figure 7: Patrick Frank's equation 6.
So, combining these two errors, his annual uncertainty estimate is √30.417 * √12 = 19 times too big. Instead of 0.382°C, it should be 0.020°C – just two hundredths of a degree! That looks a lot like the BEST estimates in figure 2.
Notice how each of equations 4, 5, and 6 all end up with the same result of ±0.382°C? That’s because Frank has not included a factor of √N – the term in the equation that relates the standard deviation to the standard error of the estimate of the mean. Frank’s calculations make the astounding claim that averaging does not reduce uncertainty!
Equation 7 makes the same error when combining land and sea temperature uncertainties. The multiplication factors of 0.7 and 0.3 need to be squared inside the square root symbol.
![]()
Figure 8: Patrick Frank's equation 7.
Patrick Frank messed up writing his equation 4 (but did the calculation correctly), and then he carried the error in the written equation into equations 5, 6, and 7 and did those calculations incorrectly.
Is it possible that Frank thinks that any non-random features in the measurement uncertainties exactly balance the √N reduction in uncertainty for averages? The correct propagation of uncertainty equation, as presented earlier from Wikipedia, has the covariance term, 2ab σAB. Frank has not included that term.
Are there circumstances where it would combine exactly in such a manner that the √N term disappears? Frank has not made an argument for this. Moreover, when Frank discusses the calculation of anomalies on page 31, he says “the uncertainty in air temperature must be combined in quadrature with the uncertainty in a 30-year normal”. But anomalies involve subtracting one number from another, not adding the two together. Remember: when subtracting, you subtract the covariance term. It’s σf2 = a2 σ2A + b2 σ2B - 2ab σAB. If it increases uncertainty when adding, then the same covariance will decrease uncertainty when subtracting. That is one of the reasons that anomalies are used to begin with!
We do know that daily temperatures at one location show serial autocorrelation (correlation from one day to the next). Monthly anomalies are also autocorrelated. But having the values themselves autocorrelated does not mean that errors are correlated. It needs to be shown, not assumed.
And what about the case when many, may stations are averaged into a regional or global mean? Has Frank done a similar error? Is it worth trying to replicate his results to see if he has? He can’t even get it right when doing a simple propagation from daily means to monthly means to annual means. Why would we expect him to get a more complex problem correct?
When Frank displays his graph of temperature trends lost in the uncertainty (his figure 19), he has completely blown the uncertainty out of proportion. Here is his figure:
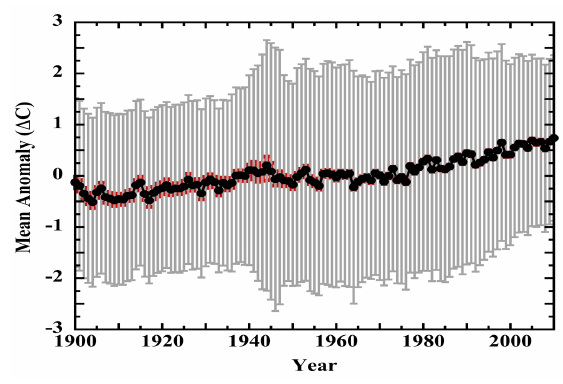
Figure 9: A copy of Figure 19 from Frank (2023). The uncertainties - much larger that those of BEST in figure 2, are grossly over-estimated.
Is that enough to realize that Patrick Frank has no idea what he is doing? I think so, but there is more. Remember the discussion about standard deviation, RMSE, and MBE? And random errors and independence of errors when dealing with two variables? In every single calculation for the propagation of uncertainty, Frank has used the formula that assumes that the uncertainties in each variable are completely independent. In spite of pages of talk about non-randomness of the errors, of the need to consider systematic errors, he does not use equations that will handle that non-randomness.
Frank also repeatedly uses the factor 1.96 to convert the one-sigma 68% confidence limit to a 95% confidence limit. That 1.96 factor and 95% confidence limit only apply to random, normally distributed data. And he’s provided lengthy arguments that the errors in temperature measurements are neither random nor normally-distributed. All the evidence points to the likelihood that Frank is using formulae by rote (and incorrectly, to boot), without understanding what they mean or how they should be used. As a result, he is simply getting things wrong.
To add to the question of non-randomness, we have to ask if Frank has correctly removed the MBE from any RMSE values he has obtained from the literature. We could track down every source Frank has used, to see what they really did, but is it worth it? With such elementary errors in the most basic statistics, is there likely to be anything really innovative in the rest of the paper? So much of the work in the literature regarding homogenization of temperature records and handling of errors is designed to identify and adjust for station changes that cause shifts in MBE – instrumentation, observing methodology, station moves, etc. The scientific literature knows how to do this. Patrick Frank does not.
I’m running out of space. One more thing. Frank seems to argue that there are many uncertainties in LiG thermometers that cause errors – with the result being that the reading on the scale is not the correct temperature. I don’t know about other countries, but the Meteorological Service of Canada has a standard operating procedure manual (MANOBS) that covers (among many things) how to read a thermometer. Each and every thermometer has a correction card (figure 6) showing the difference between what is read and what the correct value should be. And that correction is applied for every reading. Many of Frank’s arguments about uncertainty fall by the wayside when you realize that they are likely included in this correction.
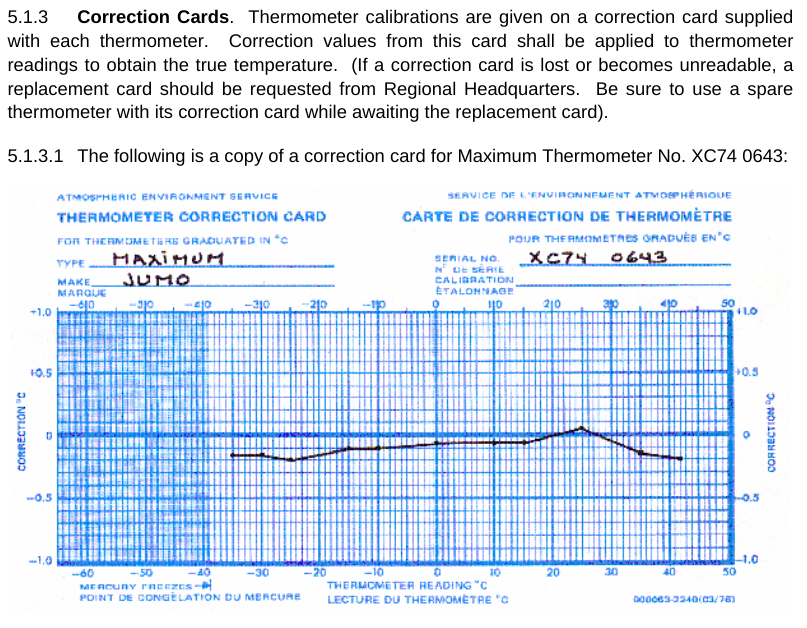
Figure 10: A liquid-in-glass temperature correction card, as used by the Meteorological Service of Canada. Image from MANOBS.
Frank’s earlier papers? Nothing in this most recent paper, which I would assume contains his best efforts, suggests that it is worth wading through his earlier work.
You might ask, how did this paper get published? Well, the publisher is MDPI, which has a questionable track record. The journal - Sensors - is rather off-topic for a climate-related subject. Frank’s paper was first received on May 20, 2023, revised June 17, 2023, accepted June 21, 2023, and published June 27, 2023. For a 46-page paper, that’s an awfully quick review process. Each time I read it, I find something more that I question, and what I’ve covered here is just the tip of the iceberg. I am reminded of a time many years ago when I read a book review of a particularly bad “science” book: the reviewer said “either this book did not receive adequate technical review, or the author chose to ignore it”. In the case of Frank’s paper, I would suggest that both are likely: inadequate review, combined with an author that will not accept valid criticism.
The paper by Patrick Frank is not worth the electrons used to store or transmit it. For Frank to be correct, not only would the entire discipline of climate science need to be wrong, but the entire discipline of introductory statistics would need to be wrong. If you want to understand uncertainty in global temperature records, read the proper scientific literature, not this paper by Patrick Frank.
Additional Skeptical Science posts that may be of interest include the following:
Of Averages and Anomalies (first of a multi-part series on measuring surface temperature change).
Berkeley Earth temperature record confirms other data sets
Are surface temperature records reliable?
Posted by Bob Loblaw on Monday, 7 August, 2023
 |
The Skeptical Science website by Skeptical Science is licensed under a Creative Commons Attribution 3.0 Unported License. |