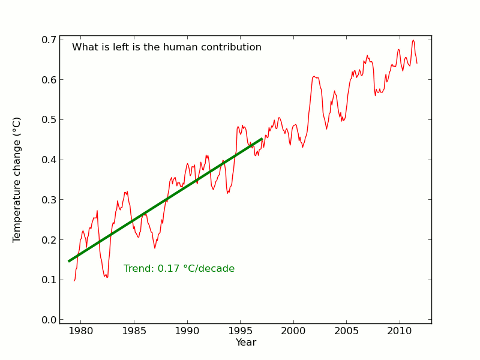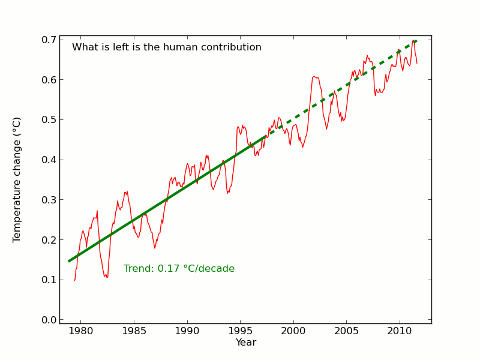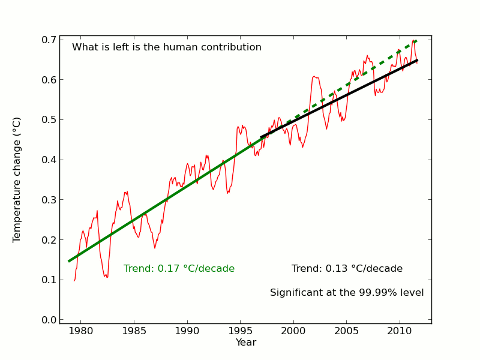
Update 21/02/2013: Troy Masters is doing some interesting analysis on the methods employed here and by Foster and Rahmstorf. On the basis of his results and my latest analysis I now think that the uncertainties presented here are significantly underestimated, and that the attribution of short term temperature trends is far from settled. There remains a lot of interesting work to be done on this subject.
The ‘16 years’ video has lead to a number of good questions from viewers which simply could not be addressed in a basic 2-minute explanation. We will first look at the results from the latest data, and then try and address some of the questions which have arisen. The main issues which will be addressed are:
Each question will be addressed at a basic level where possible, however some of the issues are more technical.
The GISTEMP temperature data for December 2012 was not available at the time the video was being made, and thus could not be included. The release of this extra month of data brought a couple of surprises: Firstly the additional month was cooler than expected, and secondly GISTEMP switched from using HadISST to ERSST for the sea surface temperature data. These both affected the results. In addition I have switched to using the constrained trend method described here for the trends reported in the text and included the latest volcano and solar data.
The result of the extra data is that there is now a visually observable change in trend pre- and post-1997, however the post-1997 trend is still significant at the 99.99% level and the change in trend does not reach statistical significance. However the visual impact is affected; the final scene would look like this with the new data:

This change in the results highlights the difficulty in drawing conclusions from such short periods - which is why most serious climate scientists avoid doing so. However given the public interest in this issue I will continue to monitor the underlying trends and report if there is a significant change, especially if the change in trend since 1997 becomes statistically significant.
In the short term I hope to annotate the video to direct viewers to this update. I will try to provide a new version of the video using the latest data and methods later in the year, however the task is time consuming and only practical during vacations.
The aim of the calculation is to subtract out natural influences from the actual temperatures to obtain an estimate of the human contribution to recent warming. Obviously if we are given a completely free choice of what to subtract out then we can get any answer we want and the exercise is meaningless. So a more rigorous approach is required.
There is a very widely used approach to this problem called ‘multivariate linear regression’, which is used across many fields of science and economics. Linear regression determines how much of each cause (i.e. natural and human influences) is required to best explain the observed effect (i.e. temperature).
Like most statistical methods linear regression can be misused to give misleading results. As more causal factors are added, it becomes easier to get a good fit by chance. Therefore only causal factors which significantly improve the fit to the observations should be used. So if linear regression is used properly we have very limited control over the answer. We can only use causal factors which are strongly supported by the observations, and we don’t get to choose how big the contributions of the various factors are: the linear regression does that for us.
In this case, the causal factors were determined by Foster and Rahmstorf, and included solar irradience (the PMOD satellite data), volcanic eruptions (from Nasa/GISS), the El Niño/La Niña oscillation (Multivariate ENSO Index or MEI), and a linear trend to approximate the current impact of human emissions (and a small correction for annual cycles). The different causal factors are shown in Figure 2: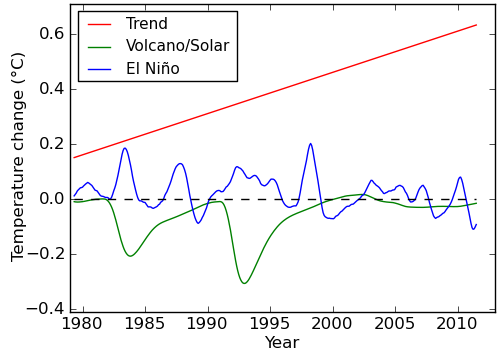
Figure 2: Estimated natural and human contributions to the temperature record, 12 month moving average.
In addition Foster and Rahmstorf allowed each natural influence to have a delay of a few months in its effect on temperature - these delays were also optimised to best explain the observed temperatures. It would be possible to add additional factors, or change the causal factors used, however any such change would need to be justified both physically and statistically.
Figure 3 shows the sum of the contributions, compared to the observed temperatures.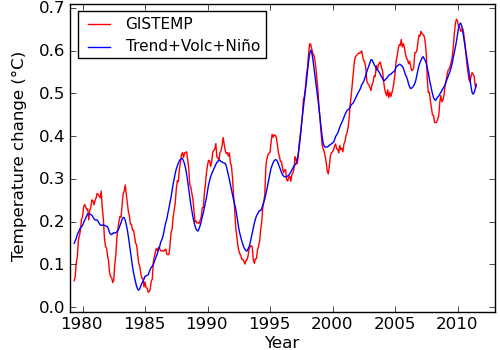
Figure 3: Sum of contributions and temperature record, 12 month moving average.
By definition, any change in the size of any of the contributions makes the fit to the temperatures worse.
In this work, two small changes were made to the Foster and Rahmstorf method. Firstly, there is a natural scale for combining the effects of the solar and volcanic influences, given by the effect they have on the amount of solar energy entering the climate system. This relationship was used to combine the solar and volcanic influences into one, reducing the amount of freedom in the calculation even further - i.e. this calculation is more conservative. This is reflected in the slightly lower final trend compared to Foster and Rahmstorf.
Secondly, instead of delaying the combined volcanic/solar term by a few months, an exponential response was used - just as an oven takes a while to get up to temperature after it is turned on, the effect of the volcanic/solar term was also made gradual. The time for this response was again optimised against the observations rather than chosen. These two changes were made to address an issue raised by Rypdal (2012) that the coincidental occurrence of volcanoes on the declining phase of the solar cycle could cause these two factors to be mis-estimated.
Are the results dependent on the choice of natural factors?
The effect of different and additional natural factors has also been examined. Instead of satellite measurements of solar irradience we can use a proxy, in this case sunspot number. Instead of MEI for El Niño we can use Nino34. In addition the effect of long term oscillations such as the Atlantic Multidecadal Oscillation and Pacific Decadal Oscillation can be tested. However care is required - adding additional terms, even noise, tends to improve the fit to the data. The AIC penalizes the addition of extra parameters to ensure that any new terms make a genuine improvement to the model fit.
| AIC |
Trend pre 1997 | Trend post 1997 | Trend difference | |
| Base calculation | -642.1 | 0.170±0.016 | 0.134±0.019 | 0.037±0.025 (<2σ) |
| MEI->Nino34 | -624.6 | 0.163±0.017 | 0.119±0.020 | 0.044±0.026 (<2σ) |
| TSI->Sunspots | -642.0 | 0.173±0.016 | 0.131±0.019 | 0.042±0.025 (<2σ) |
| Add AMO | -640.3 | 0.173±0.016 | 0.136±0.019 | 0.037±0.025 (<2σ) |
| Add PDO | -640.8 | 0.169±0.016 | 0.131±0.019 | 0.039±0.025 (<2σ) |
In every case the trend post 1997 is significant at the 99.99% level, and the trend difference is not statistically significant. None of the variants on the calculation are statistically better than the original, and in every case the conclusions are unchanged.
A similar calculation can be performed over the last 130 years rather than the past 35 years as used in the video. In this case it is no longer possible to fit the human contribution as a linear trend - instead the full range of climate influences must be used and their effect on temperature determined. The simplest way to do this is using a very simple ‘2-box model’ (Rypdal 2012) to relate influences to effects - a calculation requiring 20-30 lines of code. In this kind of calculation the speed with which temperature responds to changes in forcing is determined by finding the response times which best fit the observations. Again the result is optimised to best explain the data. This calculation includes one additional term to model the significant impact of El Niño on temperatures, which was omitted from the Rypdal calculation.
The modeled temperatures are compared to the observations using annual data from 1880-2010 in Figure 4.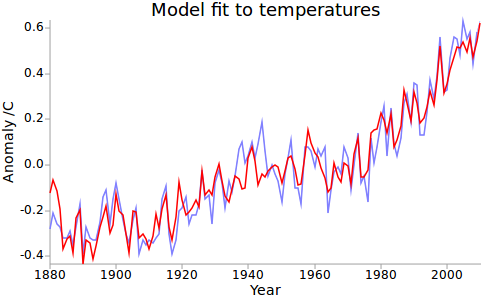
Figure 4: 2-box+El Niño model fit to temperatures over 130 years.
The fit is very good, and the model also shows a slowdown in warming since the late 90’s. The El Nino term, which is the principal factor affecting the rate of warming over the past 16 years, is actually larger than that obtained by the simpler approach.
| El Nino (MEI) coefficient | |
| Foster & Rahmstorf | 0.079 |
| 35 year calculation | 0.071 |
| 130 year calculation | 0.083 |
Using 130 years of data leads to the same conclusion.
Uncertainties in the observations
The use of a regression calculation depends on an assumption that the variance of the observations does not vary significantly - i.e. they are homoscedastic. The principal source of uncertainty in the long run temperature record is due to coverage, with substantially poorer coverage in earlier decades. GISTEMP has near-complete coverage since the establishment of Antarctic stations in the 1950s. The 2-box model calculation above was therefore repeated using just the post-1950 data. The results and therefore the conclusions are unchanged.
In fact the principal limitation of this kind of calculation lies elsewhere: The uncertainties in the forcings are far more important than temperature uncertainties in determining the results of the 2-box model. Fortunately the solar and volcanic effects behave differently from the anthropogenic forcings in that they show significant short term variations. This information might be better exploited by fitting an unknown smooth function instead of the uncertain anthropogenic forcings, and will be explored further in future.
The principle difference between the NASA GISTEMP and Hadley HadCRUT4 datasets is coverage - the GISTEMP data covers 98% of the Earth’s surface, whereas HadCRUT4 covers only 84%. The coverage of 6 temperature datasets along with an indication of the temperature change over 15 years is shown in Figure 5.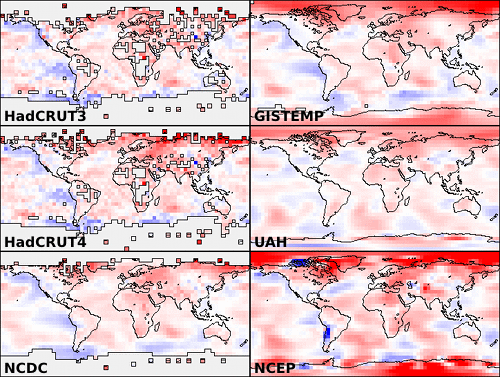
HadCRUT4 is missing the regions of the planet which, according to GISTEMP, the UAH satellite data and NCEP/NCAR reanalysis data (which combines diverse measurements in a weather model) are warming fastest. The implication is that HadCRUT4 underestimates recent temperatures. An estimate of the effect may be obtained by calculating how the UAH, GISTEMP or NCEP/NCAR temperatures would be biased if their coverage were reduced to that of HadCRUT4. The results are shown in Figure 6.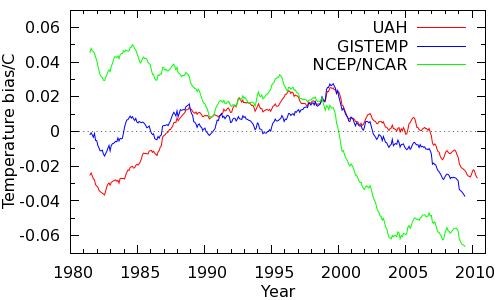
Figure 6: Coverage bias in the HadCRUT4 record estimates from various sources, 60 month smooth.
All the data sources agree that the non-global coverage of HadCRUT4 introduces a warm bias around 1998 declining to a cool bias in recent years, and thus significantly impacts the short term trend. On this basis, we expect the human contribution to the HadCRUT trend after 1997 to be biased lower than the trend prior to 1997. The trends are as follows:
| Trend ± uncertainty (1σ) | |
| Pre-1997 | 0.183 ± 0.015 C/decade |
| Post-1997 | 0.120 ± 0.018 C/decade |
| Difference | 0.063 ± 0.023 C/decade |
The trend post 1997 is lower, exactly as expected. The trend is still significant at the 99.99% level, however there is now a significant difference between the pre and post 1997 trends.
What if HadCRUT4 had global coverage? This question may be addressed by filling in the empty regions of the map from nearby temperatures. There is a good conservative method of doing this, called kriging, which learns how far it can fill temperatures by learning from the data that is already present. A preliminary application of kriging to the gridded HadCRUT4 has been made although the results are provisional at this stage. If the human contribution to the temperature trend is calculated using the global temperatures, the trends are as follows:
| Trend ± uncertainty (1σ) | |
| Pre-1997 | 0.178 ± 0.024 C/decade |
| Post-1997 | 0.152 ± 0.022 C/decade |
| Difference | 0.025 ± 0.033 C/decade |
Once again the change in trend is statistically indistinguishable from noise. When using global data there is no compelling evidence in the temperature record for a change in trend in the human contribution to global warming. Using the krigged data does introduce an interesting feature in the model - the characteristic time of the exponential lag drops from 14 months to 5 months - this will be the subject of further study. At this point it seems likely that an optimal treatment will require a combination of the two methods outlined here to exploit all of the data.
Note: Due to the time consuming nature of this calculation and the slow updating of the HadCRUT4 data this calculation still uses the Nov 2012 data, however the impact of the extra month is not expected to be so significant in this case as for GISTEMP.
Whether we use 35 years of data with the assumption of a linearly increasing human contribution to global warming, or 130 years of data using a simple forced model, the conclusion is the same - the recent slowdown in warming arises from the human contribution being partially masked by natural influences, primary El Niño. All the methods tested agree on the size of the El Niño contribution.
When applying the same method to the HadCRUT4 data, the trend in the human contribution to global warming over the last 16 years remains highly statistically significant. The incomplete geographical coverage of the HadCRUT4 data is expected to lead to a lower trend past 1997, and this is exactly what is observed. The slower warming of the HadCRUT4 data compared to GISTEMP is sufficiently explained by coverage bias.
Posted by Kevin C on Sunday, 10 February, 2013
 |
The Skeptical Science website by Skeptical Science is licensed under a Creative Commons Attribution 3.0 Unported License. |