In Part 1A we looked at how a reasonable temperature record needs to be compiled. If you haven't already read part 1A, it might be worth reading it before 1B.
There are four major surface temperature analysis products produced at present: GISTemp from the Goddard Institute of Space Sciences (GISS); HadCRUT, a collaboration between the Hadley Research Center and the University of East Anglia Climate Research Unit (HadCRUT); The US National Oceanic And Atmospheric Administration’s (NOAA) National Climatic Data Center (NCDC); and the Japanese Meteorological Agency (JMA). Another major analysis effort is currently underway: the Berkeley Earth Surface Temperature Project (BEST), but as yet their results are preliminary.
We will look first specifically at the product from GISS, at how they do their Average of Anomalies, and their Area Weighting scheme. This product dates back to work undertaken at GISS in the early 1980s with the principle paper describing the method being Hansen & Lebedeff 1987 (HL87).
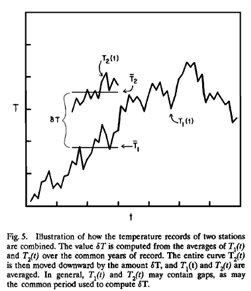
The following diagram illustrates the Average of Anomalies method used by HL87

This method is called the ‘Reference Station Method’. One station in the region to be analysed is chosen as station 1, the reference station. The next stations are 2, 3, 4, etc., to 'N'. The average for each pair of stations (T1, T2), (T1, T3), etc. is calculated over the common reference period using the data series for each station T1(t), T2(t), etc., where "t" is the time of the temperature reading. So for each station their anomaly series is the individual readings - Tn(t) - minus the average value of Tn.
"δT" is the difference between their two averages. Simply calculating the two averages is sufficient to produce two series of anomalies, but GISTemp then shifts T2(t) down by δT, combines the values of T1(t) and T2(t) to produce a modified T1(t), and generates a new average for this (the diagram doesn’t show this, but the paper does describe it). Why are they doing this? Because this is where their Area Averaging scheme is included.
When combining T1(t) and T2(t) together, after adjusting for the difference in their averages, they still can’t just add them because that wouldn’t include any Area Weighting. Instead, each reading is multiplied by an Area Weighting factor based on the location of each station; these two values are then added together and divided by the combined area weighting for the two stations. So series T1(t) is now modified to be the area weighted average of series T1(t) and T2(t). Series T1(t) now needs to be averaged again since the values will have changed. Then they are ready to start incorporating data from station 3 etc. Finally, when all the stations have been combined together, the average is subtracted from the now heavily-modified T1(t) series, giving us a single series of Temperature Anomalies for the region being analysed.
So how are the Area Weighting values calculated? And how does GISTemp then average out larger regions or the entire globe?
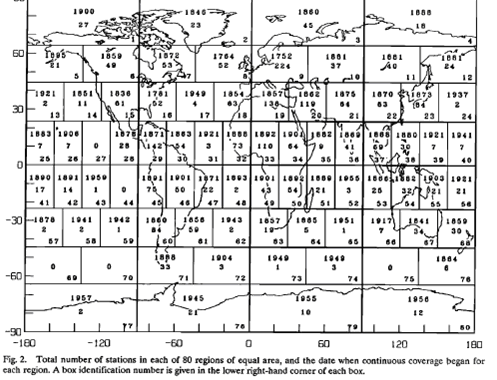
They divide up the Earth into 80 equal area boxes – this means each box has sides of around 2500km. Then within each box they divide these up into 100 equal area smaller sub-boxes.
They then calculate an anomaly for each sub-box using the method above. Which stations get included in this calculation? Every station within 1200 km of the centre of the sub-box. And the weighting for each station used simply diminishes in proportion to its distance from the centre of the sub-box. So a station 10km from the centre will have a weighting of 1190/1200 = 0.99167, while a station 1190 km from the centre will have a weighting of 10/1200 = 0.00833. In this way, stations closer to the centre have a much larger influence while those farther away an ever smaller influence. And this method can be used even if there are no stations directly in the sub-box, inferring its result from surrounding stations.
In the event that stations are extremely sparse and there were only 1 station within 1200 km, then that reading would be used for a sub-box. But as soon as you have even a handful of stations within range, their values will quickly start to balance out the result. And closer stations will tend to predominate. Then the sub-boxes are simply averaged together to produce an average for the larger box – we can do this without any further area averaging because we have already used area averaging within the sub-box and they are all of equal area. Then in turn the larger boxes can be averaged to produce results for latitude bands, hemispheres, or globally. Finally these results are then averaged over long time periods.
Remember our previous discussion of Teleconnection, and that long term climates are linked over significant distances. This is why this process can produce a meaningful result even when data is sparse. On the other hand, if we were trying to use this method to estimate daily temperatures in a sub-box, the results would be meaningless. The short term chaotic nature of daily weather would swamp any longer range relationships. But averaged out over longer time periods and larger areas, the noise starts to cancel out and underlying trends emerge. For this reason, the analysis used here will be inherently more accurate when looked at over larger times and distances. The monthly anomaly for one sub-box will be much less meaningful than the annual anomaly for the planet. And the 10-year average will be more meaningful again.
And why the range of 1200 km? This was determined in HL87 based on the correlation coefficients between stations shown in the earlier chart. The paper explains this choice:
“The 1200-km limit is the distance at which the average correlation coefficient of temperature variations falls to 0.5 at middle and high latitudes and 0.33 at low latitudes. Note that the global coverage defined in this way does not reach 50% until about 1900; the northern hemisphere obtains 50% coverage in about 1880 and the southern hemisphere in about 1940. Although the number of stations doubled in about 1950, this increased the area coverage by only about 10%, because the principal deficiency is ocean areas which remain uncovered even with the greater number of stations. For the same reason, the decrease in the number of stations in the early 1960s, (due to the shift from Smithsonian to Weather Bureau records), does not decrease the area coverage very much. If the 1200-km limit described above, which is somewhat arbitrary, is reduced to 800 km, the global area coverage by the stations in recent decades is reduced from about 80% to about 65%.”

It’s a trade-off between how much coverage we have of the land area and how good the correlation coefficient is. Note that the large increase in contributing station numbers in the 1950s and subsequent drop off in the mid-1970s does not have much of an impact on percentage station coverage – once you have enough stations, more doesn’t improve things much. And remember, this method only applies to calculating surface temperatures on land; ocean temperatures are calculated quite separately. When calculating the combined Land-Ocean temperature product, GISTemp uses land-based data in preference as long as there is a station within 100 km. Otherwise it uses ocean data. So in large land areas with sparse station coverage, it still calculates using the land-based method out to 1200 km. However, for an island in the middle of a large ocean, the land-based data from that island is only used out to 100 km. After that point, the ocean based data prevails. In this way data from small islands don’t influence the anomalies reported for large areas of ocean when ocean temperature data is available.
One aspect of this method is the order in which stations are merged together. This is done by ordering the list of stations used in calculating a sub-box by those that have the longest history of data first, with the stations with shorter histories last. So they are merging progressively shorter data series into a longer series. In principle, the method used to select the order in which the stations are being processed could have a small effect on the result. Selecting stations closer to the centre of the sub-box first is an alternative approach. HL87 considered this and found that the two techniques produced differences that were two orders of magnitude smaller than the observed temperature trends. And their chosen method was found to produce the lowest estimate of errors. They also looked at the 1200 km weighting radius and considered alternatives. Although this produced variations in temperature trends for smaller areas, it made no noticeable difference to zonal, hemispheric, or global trends.
The other temperature products use somewhat simpler methods.
HadCRUT (or really CRU, since the Hadley Centre contribution is Sea Surface Temperature data) calculate based on grid boxes that are xº by xº, with default value being 5º by 5º. At the equator, this means they are approximately 550 x 550 km, although much smaller at the polar regions. They then take a simple average all the anomalies for every station within that grid box. This is a much simpler area averaging scheme. Because they aren’t interpolating data like GISS, they are limited by the availability of stations as to how small their grid size can go, otherwise too many of their grids may have no station at all. And in grid boxes where there is no data available, they do not calculate anything. So they aren’t extrapolating / interpolating data. But equally, any large-scale temperature anomaly calculation such as for a hemisphere or the globe is effectively assuming that any uncalculated grid boxes are all actually at the calculated average temperature. However, to then build results for larger areas, they need to area weight the averages for the differing sizes of the grid boxes depending on the latitude they are at.
NCDC and JMA also use a 5º by 5º grid size and simply average anomalies for all stations within that grid then area weighted averaging is used to average grid boxes together. All three also combine land and sea anomaly data. Unlike HadCRU & NCDC, which use the same ocean data, JMA maintain their own separate database of SST data.
In this article and the Part 1A, I have tried to give you an overview of how and why surface temperatures are calculated, and why calculating anomalies then averaging them is far more robust than what might seem the more intuitive method of averaging then calculating the anomaly.
In parts 2A & 2B we will look at the implications of this for the various questions and criticisms that have been raised about the temperature record.
Posted by Glenn Tamblyn on Monday, 30 May, 2011
 |
The Skeptical Science website by Skeptical Science is licensed under a Creative Commons Attribution 3.0 Unported License. |