
This post is number 16 in a series about ocean acidification. Other posts: Introduction, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, Summary 1 of 2, Summary 2 of 2.
Welcome to the 16th post in our series about the fundamental background chemistry to ocean acidification. In the last post we introduced the solubility product, Ksp. Ksp describes the state of dissolution at equilibrium. By analogy with the K and Q we saw in post 8 we can also describe a Qsp that describes the state of dissolution when system is not at equilibrium.
To formalise this relationship and predict what will happen in a given situation we can write this as a ratio of the concentration of dissolved ions currently present in a given solution to the concentration of dissolved ions in a saturated solution. We call this ratio omega, Ω.

If Ω < 1 then the solution is undersaturated and dissolution occurs. If Ω > 1 then the solution is supersaturated and dissolution does not occur (i.e. precipitation can occur). If Ω = 1 the solution is exactly saturated and nothing happens.
We now know that the amount of ions present is given by the solubility product so we can rewrite the expression for Ω as Equations 25:

And we can, in turn, replace this with an expression specific for calcium carbonate as Equation 26:

We can now go one step further (*) because the bottom line of Eq. 26 for Ω is the same as the expression for the Ksp of CaCO3 (post 15) and the top line is Qsp for a system that is not at equilibrium:

We recall from post 13 that the 2 main polymorphs of calcium carbonate have different solubilities and so there is an Ω for calcite and an Ω for aragonite. That is, the values for the saturated concentrations of Ca2+ and CO32– are different for aragonite and calcite.
In surface seawater at 25oC and 35 salinity the Ksp (calcite) ≈ 4.3 ×10–7 and Ksp (aragonite) ≈ 6.5 ×10–7. And, as we have come to expect, each of those conditions – pressure, temperature, and salinity influence the solubility product.
The solubility of calcium carbonate increases at lower temperatures; for surface water at constant salinity a temperature change from 25oC to 5oC corresponds to a change in Ksp of ~1% for calcite and ~5% for aragonite. If you take a heap of salt or sugar and dissolve it in a cup of water you will find the water gets noticeably colder. This happens because it takes energy to shake the ions out of their stacked array. The source of the energy is heat energy from the water. This is why it is easier to dissolve salt or sugar in hot water; the water has more heat energy that can be stolen by the salt or sugar for the dissolution process. A reaction that takes in energy is called endothermic.
Similarly, a reaction that gives out energy is called exothermic and, unlike most minerals, the dissolution of calcium carbonates is exothermic it means that solid calcium carbonate is favoured at higher temperatures i.e. the solubility is greater at lower temperatures.
The effect of salinity is not so noticeable because in deep water there is little variation in salinity (though in surface waters local variation in salinity can have an impact on Ksp (including, tautologically, because "salinity" includes Ca2+ and dissolved inorganic carbon species).
Pressure also has an effect; solubility decreases with pressure. The theory behind this is way beyond a simple blog post but mostly comes down to the change in volume with pressure (this is the reason why we said earlier that it is better to use moles per kg for concentration than moles per L). So we'll simply give some values for 3000 m (at 25oC and 35 S) to demonstrate the extent of the effect. The Ksp for calcite at 3000 m is the same as the Ksp for aragonite at the surface.

The concentration of calcium in seawater doesn't change much with depth or location. This is because it has only one main source (the weathering of carbonate rocks) and, because weathering is slow, the ocean is well mixed in terms of the time scale for supply of calcium by weathering. But, as we have said, the relative concentration of carbonate species and the concentration of total carbonate species does change with depth. This is true even without a human influence.
Since the concentration of carbonate CO32– that is present decreases with depth, we can see that the ratio of present concentrations to the theoretical saturation values, Ω, decreases. Thus, we expect that Ω will decrease with depth in the deep ocean. And, so it does.
We can calculate Ω using the same deep ocean profiles we presented in post 14 for pH. If we draw a line at Ω = 1 then the depth at which this line crosses the actual Ω gives the depth below which aragonite and calcite dissolve. This is called the saturation depth or saturation horizon.
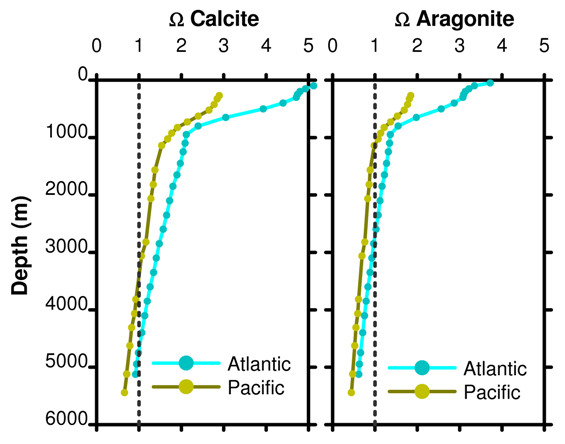
Figure 15. Depth profile of Ω for calcite and aragonite as a function of ocean basin. Data from the same WOCE project stations as the pH profile in Figure 11 from post 14.
Ω = 1 for calcite at about 3000 m and 4500 m in the Pacific and Atlantic oceans, respectively. Ω = 1 for aragonite at about 1000 m and 2500 m in the Pacific and Atlantic oceans, respectively. A poetic image used is to compare Ω to a mountain snow line; in the oceans any parts shallower than the saturation horizon will have white sediments containing calcium carbonate while the lower slopes are covered with brownish clay sediments. The real world is not quite so simple but the image is vivid and let it not be said that we will let reality get in the way of poetry.
What happens when CO2 is added to the atmosphere? Although the total amount of carbon species increases, we now know from Henry's law (post 9) and equations 7-9 (post 6 and post 7) that the net effect is to reduce the concentration of carbonate CO32– present in surface water and to leave the concentration of Ca2+ unchanged. We also know that if CO32–decreases, then Ω also decreases. That is, adding CO2 to the surface ocean will cause overall carbon to increase, but also causes the relative fraction of carbonate to decrease. In turn this decreases Ω so the profiles in Figure 15 to move to the left and the saturation horizon thus moves towards the surface, sketched in Figure 16. (Note that the future plot is not a prediction for a particular future time – we will go over such predictions in detail in the second series of posts but as a taster consider that in the Caribbean Ω aragonite is decreasing by about 0.12 per decade).

Figure 16. Conceptual plot of the saturation horizon moving towards the surface as CO2 is added to the surface ocean.

In the next post we look at how carbon is transferred from the surface ocean to the deep ocean.
Written by Doug Mackie, Christina McGraw, andKeith Hunter . This post is number 16 in a series about ocean acidification. Other posts: Introduction, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, Summary 1 of 2, Summary 2 of 2.

Posted by Doug Mackie on Sunday, 14 August, 2011
 |
The Skeptical Science website by Skeptical Science is licensed under a Creative Commons Attribution 3.0 Unported License. |