OA not OK part 7: Le Chatelier not good enough for ocean acidification
Posted on 19 July 2011 by Doug Mackie
This is post 7 in a series about ocean acidification. Other posts: Introduction , 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, Summary 1 of 2, Summary 2 of 2.
Welcome to the 7th post in our series about the fundamental chemistry of ocean acidification. In this post we shall expand on the speciation described in post 5 and consider what happens when the equilibrium of the oceans is disturbed. We will show that naive application of Le Chatelier's principle is not good enough for complex chemistry. (Following the confusion expressed in comments to previous posts we have expanded the advertised post 7 and split it in two parts.)
As we noted in post 4, the definition of an acid (in aqueous chemistry) is a substance that gives (or donates) an H+ (proton) to water to form H3O+, while a base takes (or accepts) the proton. This means that each acid (or base) reacts with a base (or acid) to produce another acid-base pair. For example, consider the dissociation of carbonic acid given in post 5's Equation 8.
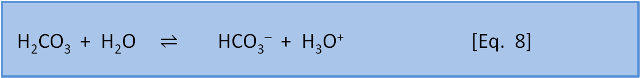
Here the carbonic acid has, not surprisingly, acted as an acid and donated an H+ to the H2O (becoming HCO3–). The H2O has acted as a base by accepting the H+ (becoming H3O+). In the reverse reaction HCO3– acts as a base by accepting H+ from H3O+ (becoming H2CO3) and the H3O+ acts as an acid by donating H+ (becoming H2O). The strength of an acid is a measure of how effectively an acid donates its proton.
We can also consider Equation 9 for the dissociation of bicarbonate to carbonate:
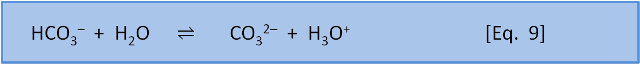
With our definition of acids we can see that bicarbonate is now acting as an acid by donating an H+. That is, bicarbonate can act as both an acid and as a base.
Chemical equilibria can be considered to be a self-balancing seesaw, pivoting around the equilibrium arrow. If one side becomes unbalanced there is a 'drive' to restore equilibrium. BUT equilibrium seldom means a 50:50 even distribution of molecules on both sides; natural equilibrium might mean a million-to-one balance.
Chemists describe the ratio of one side of a reaction equation to the other by using an equilibrium constant (K). This is the balance that a reaction will eventually reach if left undisturbed. K is calculated by using the reaction equation. For example, in the case of Equation 8 the expression is given by Equation 10:

To describe this balance the expression takes the concentrations of the products (HCO3–) and H3O+) and divides by the concentrations of the reactants (H2CO3). Note that we do not include the concentration of water (H2O) when we divide by the products. This is because the expression uses concentrations of each substance in water and the concentration of water in water is always 1 litre of water per litre of water (or whatever unit you are using).
The reason why the concentrations are multiplied is really outside the scope of a blog post. (And, in fact, for more complex salts the concentrations must sometimes be squared or cubed). At the risk of hand waving, we note that these relationships were discovered experimentally and theory caught up many years later.
However, as we have noted, such a balance is not necessarily achieved instantly. Many reactions are quite slow and so quite often a reaction system is not at equilibrium. Chemists describe the actual balance between the sides of an equation by using a reaction coefficient (Q) (Equation 11).
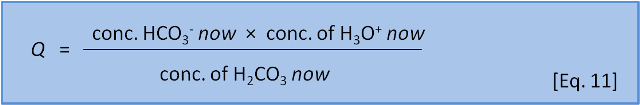
For now we will just state that K gives the ratio of products to reactants that exists when a system is at equilibrium and Q gives the ratio of products to reactants that is present at a given time before equilibrium has been reached.
Many readers may be familiar with Le Chatelier’s Principle as a way to predict how a see-saw like equilibrium reaction responds when it is disturbed. It is a useful way to consider simple reactions. However, Le Chatelier's principle only applies to single-step chemical reactions. It can't be applied in a simple way to coupled or sequential reactions.
Recall our peanut analogy for equilibrium from post 2:
Consider a dinner party with 6 people. There are 5 people on one side of the table and 1 person on the other. Each side starts with a bowl of peanuts and they begin to throw them at each other. At any one time a few peanuts will be in flight, most of them coming from the side with 5 people. However, it is plain that very quickly almost all of the peanuts will end up on the side with 1 person. At this point, the side with 5 people can only throw peanuts as quickly as the lone peanut pitcher sends them over. An equilibrium has been reached. The number of peanuts on either side does not change even though a few individual peanuts swap sides.
Now imagine that instead there is a long table. The lone peanut thrower is in the middle and there is a group at each end of the table. And, just to complicate things, at the top of the table a waiter keeps bringing in bowls of peanuts and at the foot of the table peanuts can only be thrown back if they land on the table (those landing on the floor stay there). What additional things do we need to know before we can decide how the equilibrium would change?
In our case Equations 7-9 are a coupled set of equations where the reactants (things on the left hand side) of one equation are the products (things on the right hand side) of the previous equation and both reactions are happening at the same time. For this reason Le Chatelier's Principle does not apply. Instead we need to consider the equilibrium balances for each equation.
If we look at equation 9 in isolation, Le Chatelier predicts that if a little H3O+ (i.e. acid) is added then it will force the reaction to the left side, producing bicarbonate. However, other reactions are occurring at the same time and we also need to consider equation 8. If we consider equation 8 in isolation, Le Chatelier predicts that if a little acid H3O+ is added then this should force the reaction to the left side, consuming bicarbonate.
That is, Le Chatelier predicts that adding acid both produces and consumes bicarbonate. In the next post, to solve this apparent paradox, we need to consider the equilibrium constants for the reactions.
Written by Doug Mackie, Christina McGraw , and Keith Hunter . This post is number 7 in a series about ocean acidification. Other posts: Introduction , 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, Summary 1 of 2, Summary 2 of 2.































 Arguments
Arguments

























 0
0  0
0 second summary post
second summary post







Comments