Climate Science Glossary

Term Lookup

Enter a term in the search box to find its definition.

Settings

Use the controls in the far right panel to increase or decrease the number of terms automatically displayed (or to completely turn that feature off).

Term Lookup

Settings

All IPCC definitions taken from Climate Change 2007: The Physical Science Basis. Working Group I Contribution to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Annex I, Glossary, pp. 941-954. Cambridge University Press.

Home Arguments Software Resources Comments The Consensus Project Translations About Support

Bluesky Facebook LinkedIn Mastodon MeWe

Twitter YouTube RSS Posts RSS Comments Email Subscribe


Climate's changed before
It's the sun
It's not bad
There is no consensus
It's cooling
Models are unreliable
Temp record is unreliable
Animals and plants can adapt
It hasn't warmed since 1998
Antarctica is gaining ice
View All Arguments...



Username
Password
New? Register here
Forgot your password?

Latest Posts

Archives

Are we too stupid?

Posted on 6 April 2010 by Jacob Bock Axelsen

Guest post by Jacob Bock Axelson

In a recent interview, the famous environmentalist James Lovelock bluntly stated that “humans are too stupid” to mitigate global warming. Perhaps a better question is whether or not there is any way that we can cooperate in preventing climate change. This subject has been part of the research performed by the evolutionary biologist Manfred Milinski and co-workers at the Max Planck Institute in Plön, Germany.  The Milinski group have identified that indirect reciprocity, information and perceived risk are important pieces of the puzzle. To better understand these concepts, and the results, we will briefly review the game theory of cooperation. Before we begin I should mention that cooperativity may have very strong switch-like dynamics e.g. whereas an agency with thousands of workers and engineering PhDs can produce low risk manned lunar flights, infinite individual geniuses cannot. Therefore, evolution has favoured cooperativity in biophysical mechanisms such as membrane formation, enzyme kinetics, protein folding, genetic regulation, cellular interaction and flock behavior.

In 1968 Garrett Hardin addressed the issue of misuse of common goods in the famous paper entitled "The Tragedy of the Commons". The paper created enormous controversy and has thus been cited more than 3608 times in the scientific literature (according to ISI Web of Knowledge). Hardin’s idea was based on the premise that the cost of individual use of common goods is distributed to the community. Individuals may then act according to their misguided self-interest and utilize any common resource to depletion – an individually undesirable state. Hardin mentions that psychological denial is evolutionary favorable and states: "The individual benefits (...) from his ability to deny the truth even though society as a whole, of which he is a part, suffers." Thus, one may regard the tragedy-of-the-commons partly as a consequence of individual illusory superiority (also known as the Dunning-Kruger effect). As it were, the ancient greeks had already identified some problems of unlimited freedom, in 1624 the poet John Donne wrote the famous phrase "no man is an island, entire of itself" and in 1882 the playwright Henrik Ibsen wrote the play "An Enemy of the People" on the problems of dealing with pollution. More interestingly, many native peoples are known to have somewhat successfully managed common resources such as the active use of wildfires by native Americans.

In 1971 Robert Trivers coined the term "reciprocal altruism" or "you scratch my back, I scratch yours" as a short description of the mechanism of rewarding someone for their good deeds (Trivers 1971). Major progess was seen when Axelrod and Hamilton let academics write strategies for computer tournaments and subsequently published the results in the famous paper "The Evolution of Cooperation" in 1981. The question was: what is the optimal strategy when a group of generally unrelated individuals play the Prisoner’s Dilemma (see figure below) over and over again?



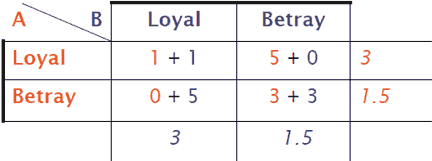
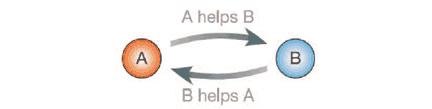
Figure 1: Top: Prisoner’s dilemma punishment matrix (years in prison per game). ‘Loyal’ means that you do not reveal information about your friend and ‘Betray’ means that you help the police. The colors and sums shows the consequences of the player’s choices. By minimizing the personal average punishment (in italics) the game thus reaches the stable Nash equilibrium of snitching. Contrary to this, the unstable Pareto optimum is that both are loyal because at least one prisoner will be unhappy with exchanging their 1-year sentence with 5 or 3. Bottom: the tit-for-tat (direct reciprocity) strategy.

The superior, strikingly simple, strategy was conceived by the mathematical psychologist Anatol Rapoport, whom had worked on the Prisoner's Dilemma for years. The strategy was that you should initially cooperate and then reciprocate your opponent i.e. start by being nice and then do what your opponent did to you last time - also known as direct reciprocity. The strategy was termed "tit-for-tat", which in the nuclear arms race had an extreme cousin known as "mutual assured destruction" and it bore resemblance to the legal concept "eye-for-an-eye" found in the Torah.

The result seemed to explain the emergence of cooperation if it were not for the fact that the dynamics in this simplified setup is highly unstable and prone to enter a "tragedy of the commons"-like scenario. Say a single one-time misunderstanding occurs: you misunderstand and think you have been cheated so you will cheat in the next round thus spurring more cheating of your partner. The “tit-for-two-tats” strategy proposed by Axelrod partly solved this instability problem. Many other strategies have been proposed amongst which the “win-stay lose-shift” (or Pavlov) strategy by Nowak and Sigmund (1993) performed markedly better in the long run than various tit-for-tat strategies. Put simply, by acting ‘as per reflex’ you could avoid sharp retaliations caused by misunderstandings.

The next major contribution was again made by Nowak and Sigmund (1998) when they studied the aspects of indirect reciprocation in evolutionary learning games. The game is the same as the Prisoner’s dilemma, but some players may now choose to punish, or discriminate against, the defectors. The inclusion of such indirect reciprocity inevitably complicates the understanding of the dynamics (see figure 2 and 3 below).


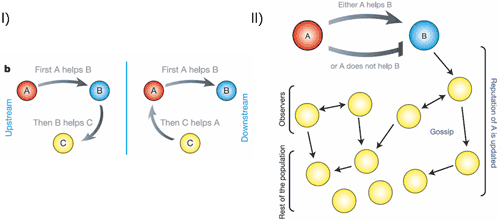
Figure 2: I) Indirect reciprocity. II) Building a reputation in the population affecting your future. Nowak and Sigmund (2005)


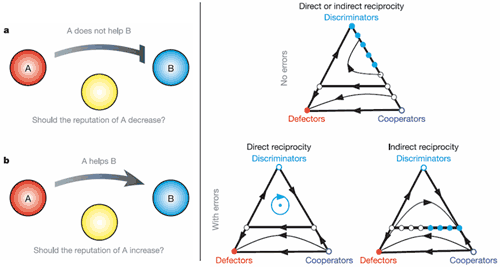
Figure 3: (left) Problems with indirect reciprocity. B has recently not helped anyone i.e. defected for some time. Should C altruistically sacrifice reputation by not helping A if A logically does not help the defector B? (right) The dynamics of a simplified game of “the good, the bad and the discriminator”. The triangle is a phase portrait i.e. the time evolution of the ratios of each type of player. Note that without sufficient discriminators/punishers everybody ends up defecting (the red lower left corner is the final outcome for the lower part of the combinations of player types). Nowak and Sigmund (2005)

All of the above is purely theoretical and somewhat confusing. Therefore there has recently been a strong interest in performing experiments with real test subjects. In 2005 Milinski and co-workers let students play a new kind of common goods game where funds are pooled to invest in mitigating climate change (Milinski 2005). They found that a finite - probably insufficient - level of altruism was always present in a population. If players were also enlightened with expert knowledge on the climate they even cooperated significantly more. Furthermore, allowing participants to take reputation into account and use indirect reciprocity also lead to cooperation comparable to publicly displaying the players’ level of altruism.

In 2008 the Milinski group found that only if disaster was 90% certain, i.e. the individual would suffer irreversible losses, could humans be motivated to reach a given target of total required preventive investments (Milinski 2008).


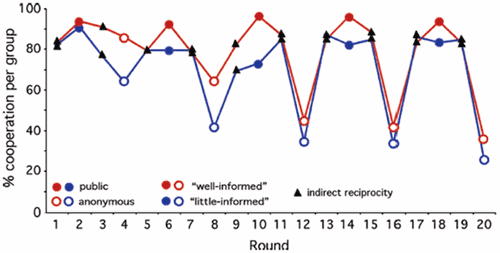
Figure 4: Results of the climate change game with real humans. Students were initially given an amount and in subsequent rounds asked to invest in a common climate pool. Filled circles were when investments were done publicly and open circles for when the investments were anonymous. The triangles was rounds when players was allowed to see each other’s investment history and decide to help each other. Red is for enlightened participants and blue for unenlightened. Blue open circles then gives a (slowly decreasing) basic level of altruism. Milinski et al. (2005).

In conclusion, theory and experiment indicates that we may be able to cooperate on climate change if a) social punishment is strong and active and b) the population is sufficiently enlightened about the facts and c) everybody knows that they will pay a price if they do not contribute in time. Lovelock probably knows this and simply finds the demands too high. In any case, the minimum 10-20 years it could take to replace the use of fossil carbon is the time it will take to reveal most of the final answer.

0 0

Printable Version  |  Link to this page

Comments

Prev  1  2  3  Next

Comments 51 to 100 out of 140:

  1. embb accuses me of setting up a "convenient straw man" in blaming the Oil Industry for the bulk of the skepticism out there. In truth, I'm just telling it as I see it. Look at the evidence: Exhibit A: Heartland Institute. Major skeptical organization, has received funding from the Fossil Fuel industry over the years-particularly Exxon. Exhibit B: George C Marshall Institute. Major skeptical organization which receives money from Exxon, amongst others, & has a former Exxon lobbyist, William O'Keefe, as its CEO. Exhibit C: Global Climate Coalition. Another Skeptic Organization-now defunct-had members from a number of large oil & automobile companies, as well as a lobbyist for Exxon. It also received considerable funding from the Oil industry in particular. Exhibit D: The Lavoisier Group. Key members are current or former members of Western Mining Corporation, Alcoa & other coal/mineral companies. Exhibit E: major skeptics, such as Ian Plimer, William Kininmonth & Garth Paltridge are all members of the group named in Exhibit D. So we see that, though not the source of *all* skepticism, the oil, coal & aluminium industries are definitely deeply involved in the skeptic "movement"-mostly because action against climate change will go against their short term interests. This isn't a straw man, its just THE FACTS!
    0 0
  2. Riccardo, I totally agree. And I would add that you're not able to (individually) find a way out of the Tragedy of the Commons even if you are aware of it. Try to picture the fisherman that notices his results diminishing, and he knows it's because of overharvesting. If he chooses to fish less, he will suffer the cost of this decision, and he will not increase the chances of perpetuating the resource (in the individual decision). Chances are, he will only leave more fish for other fishermen to overharvest. Our fisherman, alone, may choose to go on fishing even if he values the long term. The only way out is to articulate a rule of use of the resource - collectively- and find a way to enforce it. I'd say CO2 emissions are on the high end of difficulty for this kind of game. Worldwide, difficult to monitor, no direct or immediate consequences to the cheater... It's so diffuse that you have whole countries attempting to free-ride. I again suggest Elinor Ostrom's work. She even uses Game Theory as an initial test hypothesis - it's useful, but human behavior proves to be more complex than that.
    0 0
  3. Ostrom's research summarized in the Wikipedia page.
    0 0
  4. oops. for some reason, the link above came out wrong. Here's the right link to Ostroms Wikipedia page.
    0 0
  5. gallopingcamel writes: You mention CO2 "lagging". I think that fact alone destroys the idea that CO2 provides dominant forcing for global temperatures. When temperatures are rising, CO2 gets released into the atmosphere ~600 years later, nudging temperatures higher still. I'm really disappointed and frankly discouraged that you'd bring up this "lag proves that CO2 doesn't cause warming" claim. I would expect that from someone whose only familiarity with climate change issues is coming from websites like WUWT. I wouldn't expect it from someone like yourself who's spent many days reading and posting on this site. John Cook explains why CO2 lags temperature in the Pleistocene glacial/interglacial record here: CO2 lags temperature - what does it mean? It was also the subject of a blog post from just a few months ago (Why does CO2 lag temperature?). More recently, the subject of the CO2 time lag came up in this thread. One commenter suggested that in the paleoclimate record CO2 has never led temperature, always lagged. I responded by (a) explaining that this is an illogical argument, and (b) there have been many cases where CO2 changes preceded (and caused) changes in temperature. There are lots of other relevant comments in that thread as well. In fact, you yourself were part of that discussion! Help us out here, GC. What can we do to keep the same mistaken claims from popping up over and over and over again? I'm sure you're not deliberately trying to be provocative. So what's up?
    0 0
  6. Alexandre "Our fisherman, alone, may choose to go on fishing even if he values the long term." Axelrod shows that a cluster of cooperating individuals can displace the defectors and persist against mutations, making tit-for-tat evolutionary stable. In other words, the fisherman could try to convince a small group to put trust in him. He can also make the consumers discriminate against the defectors through indirect reciprocity by them favoring the single cooperator. This might not be hard as the consumers are also interested in a steady flow of fish in the future. "The only way out is to articulate a rule of use of the resource - collectively- and find a way to enforce it." This is the coercion option Hardin finally resorts to in his paper. Not having the results of Axelrod and followers he still faces the problem of how to agree on the necessary reform. "I'd say CO2 emissions are on the high end of difficulty for this kind of game. Worldwide, difficult to monitor, no direct or immediate consequences to the cheater..." It is clearly safe to say that it is a hard problem. This is why Milinski's results are so interesting: it can be handled using indirect reciprocity alone. It is not easy to hide a coal power plant, so this may be published. The media attention will affect the legislation and thus the defecting country can be indirectly punished by regulating consumer patterns.
    0 0
  7. I have just realised that I viewed a "tragedy of the commons" firsthand. May be off-topic - let the moderator decide. My family came in a long line of West of Ireland sheep-farmers in hilly country (think of the Scottish highlands). While the lowlands were divided up and walled, the upper hill slopes were known as "commonage". Those with commonage rights could graze their sheep there, and had "turbary" - the right to dig peat from the bogs for winter fuel. My father was a large landowner (he counted as a "rancher":)) I can remember plenty of land conflicts, but never one that involved the commonage. The areas were we had commonage, associated with the purchase of adjacent land, I could not grasp - but my mother claimed she knew every inch. How was the commonage so well policed? I think because all the conditions conditions Jacob mentions were in place: a) social punishment - a family overstocking the commonage would receive strong social sanction, not to mention finding their sheep had mysteriously jumped off a cliff. b) the population is sufficiently enlightened about the facts - there was a accepted social equality among the sheep-farmers, & a great spirit of assistance at lambing and sheep-shearing. It was not all about fear of a). c) everybody knows that they will pay a price if they do not contribute in time. The "laws" of the commonage were ingrained in custom, and the sanctions were well known. So where was the tragedy? Well, it came about through an external source - the European Union. Through the Common Agricultural Policy, farmers started to receive "headage" grants for the number of sheep they owned. This encouraged overgrazing. Furthermore, EU law did not recognise "commonage", so farmers were encouraged to formally divide the slopes into plots of land like the lowlands. It has come to pass that the remaining farmers (in the larger holdings)are dependent on handouts, the slopes overgrazed and the lakes polluted by sheep droppings. It was not exactly as Hardin imagined it, because the farmers were persuaded by an outside source (politicians, government advisers, lawyers) rather than self-motivated. But it was close enough. Also, the older "commonage" was not Utopia. Most of the small farmers had uneconomic holdings and were dependent on small handouts anyway (known as "farmer's dole"). But, environmentally, the unwritten commonage rights brought about better land management than modern, formal legal rights. My questions are: Is there a lesson here? What would a modern libertarian or legal positivist make of all this?
    0 0
  8. Jacob #56 Axelrod shows that a cluster of cooperating individuals can displace the defectors and persist against mutations, making tit-for-tat evolutionary stable. In other words, the fisherman could try to convince a small group to put trust in him. I´ll try to find the time to have a look at Axelrod´s paper. Ostrom´s research finds something different: even though she detects that impulse of autruistically staying within the rules, when you don´t have means to enforce the rule, in her lab experiments and field research, this usually collapses as free riders appear more and more. Of course, some means to "enforce the rules" can be some informal, cultural behaviour like diminishing one´s reputation or maybe some physical harassment. This has been observed in small fisher communities, for example. But I don´t see this working in some nationwide scale, let alone worldwide. BTW, in environmental issues I have never seen any successful case of solving air pollution without proper legislation. This is the coercion option Hardin finally resorts to in his paper. Not having the results of Axelrod and followers he still faces the problem of how to agree on the necessary reform. Coercion is a necessary part of any law. The most successful stories involve the users themselves working out an agreement (even if they resort to the state´s coercive power to enforce it). To reach the agreement can be difficult, but it´s a necessary step. You see any alternative? This is why Milinski's results are so interesting: it can be handled using indirect reciprocity alone. I assume you mean some kind of voluntary action that would lead to the agents "preferring" to stay within the rules (even if informal rules). I don´t see this happening in large scale (nation, world). And I don´t know any success stories with something as diffuse as air pollution. Think of car gas emissions - that´s only within a city, and I´ve never seen a city controlling this kind of pollution with indirect reciprocitiy alone.
    0 0
  9. Alexandre I assume you mean some kind of voluntary action that would lead to the agents "preferring" to stay within the rules (even if informal rules)(...) I don´t see this happening in large scale (nation, world). The problem, of course, is that on the other hand coercion for nations could mean war. Lovelock actually mentions this in his interview. And you are right about the problem of air pollution. In fact, handling particle filters on diesel cars has turned out to be hard to control even with laws. The setup in Milinski's first game is that the collected funds will be used to publish a notice in the newspaper about the study. The more funds the bigger the notice. Admitted, a poor substitute for the cost of investing in sustainable energy sources, but it gets interesting because it makes the players cooperate much more when using indirect reciprocity and/or informing them. The reason indirect reciprocity has not been applied yet is because these results are rather recent. With social networking media for an entire young generation in place, perhaps social peer pressure could be much stronger than for us. I have already read newspaper stories about the difference in culture of young people e.g. being upset about leaving appliances on stand by, using less water, sorting trash etc. The children will naturally be better educated than our contrarian generation, so enlightenment is implied.
    0 0
  10. My last posts on this thread (#42 & 43) caused quite a reaction. While I don't like to disappoint my fans, I have some new courses that start next week so I have some preparation to do. One has to stay at least a week ahead of the students! My regard for this blog and its denizens remains undiminished so I plan to return when the pressure of work eases. I don't want my last post to be disagreeable so I will refrain from offering any opinions. All I ask is that you view a video. This is not an unreasonable request as many of you ask me to read material that you consider important. Here is the link: http://www.youtube.com/watch?v=AHs2Ugxo7-8 This video covers the science relating to the availability of fission fuels; the effects of mining activities on the environment; "burning" high level nuclear waste; reactor safety issues; reducing plutonium production; truck mounted reactors and much more. I see "4th generation" nukes as something that both sides of the AGW debate could support. Am I wasting my time and yours?
    0 0
  11. There is a ugly practical side to this question - when it comes to a mutually binding agreement it has to be seen as "fair". Now, emerging industrial nations like China or Brasil will definitely use the non-sensical argument that the "West" caused the problem so fair means that they should get a bigger share of the commons. This argument can also be used to reject any kind of emission control, and where does that leave us?
    0 0
  12. Gallopingcamel: it is even nicer - there is a real possibility of using thorium as a nuclear fuel, and there is plenty of it.
    0 0
  13. Jacob: "The reason indirect reciprocity has not been applied yet is because these results are rather recent. With social networking media for an entire young generation in place, perhaps social peer pressure could be much stronger than for us." The point is, you need the same young generation applying the same peer pressure in China. Do you see that happening?
    0 0
  14. embb The point is, you need the same young generation applying the same peer pressure in China. Do you see that happening? No, because of censorship of the media. I was mostly thinking of societies where public opinion and public policy making is correlated. I do not think indirect reciprocity is the holy grail. However, something new is called for and tests show that it works specifically for this huge public goods game.
    0 0
  15. Commenters in this thread have discussed the problem of population growth. In that respect it might interest the audience that many economists are coming to the sobering realization that the era of continous economic growth is probably soon coming to an end: Degrowth Conference Barcelona 2010.
    0 0
  16. wrt the nuclear issue fast breeder reactors (Gen IV) use existing wastes as fuel and only 1% remains as waste, compared with 99% of Gen II reactors. Nuclear is safer than coal. The only real problem is that nuclear is still more expensive. Barry Brook's Brave New Climate is a well informed pro nuclear site based on the premise that AGW is a real problem. Also Tom Blee's book Prescription for the Planet is an interesting read mainly for his knowledge of the Integral Fast Reactor but he has other interesting ideas too, such as the boron fueled car.
    0 0
  17. Jacob:"I was mostly thinking of societies where public opinion and public policy making is correlated." well, this qualifies as a "pious wish" for me. The game participants are states, so any factor that will weaken the position of one participant will simply provide an advantage for the other - so in effect the social peer pressure can do a LOT of harm, even to the climate.
    0 0
  18. embb The game participants are states, so any factor that will weaken the position of one participant will simply provide an advantage for the other... Correct, because you are proving why the Nash-equilibrium is stable in the Prisoner's Dilemma. This calls for a strategy to maximize cooperation, as Axelrod did. The protracted conflicts around the world, where 'eye-for-an-eye' is used, shows that this is not a good way to handle such dilemmas. Therefore, perhaps indirect reciprocity between states is a solution: "you are using coal when producing goods exported to country X, so we will put a tax on imports of goods from your country and convince some of our fellows in the EU, OECD, UN, G8, G20 etc. to do the same." Wishful pious thinking is easy. All I have done is to outline proven theories and the findings of experiments that I found are quite powerful. I think the best counterargument must be real world examples of where indirect reciprocity did not work for humans or states.
    0 0
  19. Jacob:"you are using coal when producing goods exported to country X, so we will put a tax on imports of goods from your country and convince some of our fellows in the EU, OECD, UN, G8, G20 etc. to do the same." So, basically you say that economic sanctions are the way out of the "tragedy of the commons"? How realistic is that? Any example where sanctions actually worked? Are we talking about a trade war against climate offenders?
    0 0
  20. embb, Paul Krugman addresses your point nicely in his essay this past week Building a Green Economy. Scroll down to the section heading "The China Syndrome." If a country imposes anti-pollution costs on its own manufacturers, it can charge a tariff on imports from countries that don't internalize those costs, as long as the tariff is comparable to the cost borne by domestic producers (i.e., the tariff must be imposed fairly). This point is discussed in some detail in a recent World Trade Organization report on climate change. From the Executive Summary: These rules permit, under certain conditions, the use of [border tax adjustments] on imported and exported products. Indeed, border adjustments on internal taxes are a commonly used measure with respect to domestic indirect taxes on the sale and consumption of goods, such as cigarettes or alcohol. The objective of a border tax adjustment is to level the playing field between taxed domestic industries and untaxed foreign competition by ensuring that internal taxes on products are trade neutral. [...] The general approach under WTO rules has been to acknowledge that some degree of trade restriction may be necessary to achieve certain policy objectives, as long as a number of carefully crafted conditions are respected. WTO case law has confirmed that WTO rules do not trump environmental requirements. There's more detail in the body of the report. If you google this subject, you'll find the Chinese government has been arguing strenuously against this, and to some extent business media (e.g., the US Wall Street Journal) have tended to reflect this, claiming that tariffs would be "against WTO rules." But the WTO itself says there's no problem as long as foreign imports are just being charged the same cost that is borne by domestic products.
    0 0
  21. embb So, basically you say that economic sanctions are the way out of the "tragedy of the commons"? How realistic is that? Any example where sanctions actually worked? Sanctions comes on a scale and they are targeting problems on a scale. 'Oil-for-food' was a clear example of a mismatch between punishment and target. In fact, sanctions probably work more often than not. A counterexample would be something like exposing malpractices in production such as sweatshops or poisonous additives in one country and then sanctions such as taxes or legislation in the country of import were ineffective. As Ned mentions above, China knows very well that such measures works. In fact, I think economic sanctions are working so well that most of the humans in the developing world, particularly the ones with corrupt governments, have been affected unfairly by them.
    0 0
  22. This is a nice summary of the reasoning in Krugmans article: "To the objection that such a policy would be protectionist, a violation of the principles of free trade, one reply is, So? Keeping world markets open is important, but avoiding planetary catastrophe is a lot more important." There is nothing that is more important then avoiding a planetary catastrophe right? You can substitute anything to the phrase "keeping world markets open" and the sentence would be just as right or false. It is also interesting how there is a selective optimism/pessimism bias in all these arguments. Geo-engineering is sure to go wrong - and any social engineering is sure to have no negative impact, as if the precautionary principle could only be applied very very selectively.
    0 0
  23. embb Geo-engineering is sure to go wrong - and any social engineering is sure to have no negative impact, as if the precautionary principle could only be applied very very selectively. According to the Milinski papers all it takes is letting people discriminate against the ones who defies scientific evidence - much like discrimination against criminals. That can hardly be considered social engineering from a historical perspective. If one finds the consequences of global warming exaggerated, then being in favour of geo-engineering would constitute a contradiction. If one does not accept climate science, the consequences of geo-engineering cannot currently be scientifically calculated. If climate science is correct and the consequences are perceived as dire, then there is no good reason to significantly increase the risks by attempting geo-engineering on top of the problems. That is, unless in an emergency where CO2 reductions alone would not suffice.
    0 0
  24. This to me goes to show that websites like this one are doing their bit by working on requirement b) “the population is sufficiently enlightened about the facts”.
    0 0
  25. Let's say that we assume that unchecked emission of carbon dioxide will be calamitous. It seems that there are three possible approaches. 1.Current conservation approaches a la Kyoto. Negatives: They emphatically do not work and/because they are too expensive. Not only do some countries currently opt out, countries that have signed on don't do much(if any) better over the long term than countries that have opted out. Last I checked, even the countries with the "greenest" economies (like the Europeans) are still *increasing* their fossil fuel emissions. These approaches will only get more expensive as time goes on, as well. One can assume generally that the easiest, cheapest and hence, most effective changes came first. It follows thusly that as time goes on changes that reduce emissions of fossil fuel will become progressively more and more difficult and expensive, per amount of carbon removed from the atmosphere. A strategy that isn't working now and will become more and more difficult to apply in the future strikes me as a very poor one. Cost: very high. 2.As was raised earlier, we do have at least one possible option with current technology -nuclear power. Negatives. Pollution and security. Compared to 1, though, nuclear works and will continue to work as well or better as now in the future. Cost: moderate. 3. Rely on technological change to solve the problem, see below (solar power is specifically discussed at about 5:40 but the whole talk is useful to put this in context). Negatives: We don't know for sure that new technologies will continue to improve in the future as they have in the past(though it seems pretty likely that they will). Cost: Moderate. http://www.ted.com/talks/ray_kurzweil_announces_singularity_university.html Personally, I would submit that it would be "stupid" to use 1 as our primary response to the hypothetical calamity of AGW, yet that is the one that is *overwhelmingly* being advocated, even though it hasn't worked so far and will continue not to work for the foreseeable future. The "smart" response IMO would be to focus on 2 for the short to medium term and rely on investment in research on option 3 to provide for the long solution, relying on #1 as only a small and relatively unimportant part of the global warming solution. However, I personally think that 1 will continue being the popular response to AGW. This may be because people are stupid or more likely IMO that most folks use the AGW issue for other (political) issues. Cheers, :)
    0 0
  26. Shawnhet, I'd say that if one accepts continued dumping of C02 as a threat and sees #2 and #3 as solutions, they'll not be delivered as long as we continue pretending that fossil fuels are cheaper to use than reality increasingly suggests. Who is going to invest sufficient money in nuclear, wind and photovoltaic systems while the market is setting an unrealistically low price on fossil fuel consumption? To use an analogy that not only is becoming tired but remains disgusting, if I'm allowed to dump my sewage in my neighbor's yard for seemingly for free and am offered the voluntary choice of spending more money to put it in a municipal sewage system, what does human nature tell us will happen? It's not likely I'll do anything, until fecal bacteria begin showing up in my well, that's what. Not enough grownups in the room, that's the problem with C02. See Krugman's recent essay about ways we can begin playing as adults.
    0 0
  27. Doug, feel free to propose a tax increase on fossil fuels, if you want, but I feel that this is clearly a type 1 option(it's not going to work now, and it will be increasingly difficult to make it work in the future). European countries have high fuel taxes along with increasing GH emissions, so I don't think that carbon taxes will work. IAC, it is clearly not an either/or proposition, we don't need to tax carbon emissions further to build nuclear power plants or invest in solar power. We can do both right now and both will be much more effective than your proposal IMO. Cheers, :)
    0 0
  28. Shawnhet, I'm not sure where you're getting your EU emissions data but what I'm looking at shows an essentially flat total GHG emissions graph. Depending on what member state you view, you may find upward or downward emissions, but if by "European" you mean the EU I'd say the collective effort they're making is working sufficiently to arrest increases in emissions and of course this is just the beginning as far as they're concerned. As we know, that effort includes some powerful nudges from regulators. And guess what? The lights are still on in Europe, productivity figures equal or exceed our own, they're not huddled in mud huts. EU emissions data from the European Environment Agency. Now folks who are really serious about this stuff will point out that the EU has "exported" GHG emissions in various forms, mostly by accident, but one can hardly blame the Europeans for being unable to dictate how other parts of the world square up to their own responsibilities. Lord knows, they've tried their best to urge the rest of us to get our act together. Others may say that confounding factors such as collapsing Eastern economies make the EU emissions scene unrealistic, but at the same time we have some outliers (Italy, Spain) that have more than helped offset those events. In any case the absorption of Eastern states has largely receded into the past, those economies have adopted some habits that considered correlated with improving lifestyles, yet we've still got a flat graph to look at out of Europe. So I think the picture you paint is entirely too simple and is contradicted by empirical evidence.
    0 0
  29. Oops. When I said "productivity figures equal or exceed our own" I implied "our" as the U.S.A., ~4.5% world population.
    0 0
  30. Doug, here are a couple of references laying out the increased emissions from Europe. http://www.eea.europa.eu/pressroom/newsreleases/GHG2006-en http://ecopreneurist.com/2008/04/03/2007-european-carbon-dioxide-emissions-rise-11-carbon-futures-jump-39/ http://www.pbl.nl/en/news/pressreleases/2009/20090625-Global-CO2-emissions_-annual-increase-halved-in-2008.html Very recent numbers are affected by the economic downturn, of course. IAC, a flat rate isn't good enough if the theory is accurate, the recent US rate is pretty comparable to the European one. To prevent the proposed calamity, we would actually need to *reduce* the amount of CO2 emissions. So Europe will have to do *more* if you are right(bearing in mind of course that one of the reasons for EU's low carbon emissions is nuclear power). As I have said, it will be increasingly difficult to get them to do so. Again, far from being contradicted by empirical evidence, my POV is confirmed by it. Cheers, :)
    0 0
  31. I'd certainly prefer to see steadily declining GHG emissions in the EU, shawnhet, but your highlighting of 2 years' data and further remark on economic activity demonstrates yet again how it is a mistake to build a case on selected datapoints, noisy as they are. Using the data at the link I provided above, you can see that despite numerous swerves in economic activity and massive changes in regional geopolitics, the EU's GHG emissions trend is downward. During this period the EU as well as member states acting independently have introduced a number of aggressive schemes to limit GHG emissions. By so doing, a generous assessment is that they have if nothing else arrested the emissions trend we see in other parts of the world with looser regulations. A more pessimistic interpretation might emphasize the declining curve of reductions; that may be a matter of initial incentives running their course and leading to the steepening curve of effort you alluded to. However, your basic assertion of increasing EU GHG emissions does not have a firm foundation.
    0 0
  32. Doug, whether the trend is slightly downward or flat or slightly rising, the *big picture* is that in order to avoid the hypothetical catastrophe *significant* **reductions** in CO2 will have to be forthcoming. As I have said, those reductions will be increasingly difficult to come by. Most of the easy stuff has already been done. So what? Do you want to keep focusing on efforts that will be increasingly difficult to receive any sort of payout or do you want to focus on the stuff that has a chance to work? Does it make any sense to complain about others stupidity and ignore doing the easy stuff? Cheers, :)
    0 0
  33. Most of the easy stuff has already been done, shawnhet? I'm not so sure about that, if you run the numbers you'll see the EU is choosing to do some of the hard things first, a little prematurely, when they're too expensive. Take photovoltaic systems, for instance. Some EU countries have made the choice to invest in these early, which has helped to build manufacturing capacity but has I think been a poor choice of where the first funds directed to eliminating our fossil fuel habit should go. PV systems are still relatively expensive, dollar per watt, compared to some other technologies that are proven useful and waiting for deployment. For example, the EU like many other places has a substantial requirement for domestic hot water (sorry, one of my favorite grinds) as well as space heating. DHW and space heating systems require low grade heat of the sort not required to do "work" in the sense we're accustomed to. This sort of energy is extremely easy to capture using solar input and it also happens to be relatively easy to store. Because this technology is both very efficient at capturing sunlight and as well requires nothing particularly special in the way of manufacturing capabilities, it is potentially extremely affordable compared to PV systems. N. Europe is not a place where solar heating of water can be accomplished year 'round but nonetheless a substantial portion of energy input to heat water waits to be offset by augmentation of existing systems with solar input. The watt-equivalent contribution this adjustment can make to relieving load from the electric grid comes at about a tenth the price of watts captured via PV systems. Meanwhile, a liter of water heated 10 degrees centigrade does not care whether it was heated by electricity, natural gas or solar radiation, but we obviously should be when confronted with comparative numbers of 10:1. This matter of inverted priorities w/regard to solar energy capture will be noticed, is in fact being noticed now. Given that at the end of the day most water in Europe is ultimately heated via natural gas, we see there is actually a substantial amount of carbon being emitted by the EU that will be relatively easy to eliminate. This is assuming that regulators stimulate the private enterprise needed to produce DHW and space heating solar capture systems at sane production levels and hence prices, instead of the hobbyist level the industry occupies in much of the EU north of Spain and Greece.
    0 0
  34. And by the way, ahawnhet, you've left hanging the question of how and why-- without encouragement and full information-- free markets will choose non-legacy energy systems that are allowed to be mistaken as more expensive? -- How in the absence of full and transparent accounting for all costs whether that accounting be done voluntarily or otherwise will the free market make the correct choice, the one that is most economically efficient in the long term? -- Knowing of external costs that are presently ignored in pricing, how does the free market adjust the price of legacy energy liberation systems to reflect their true cost?
    0 0
  35. Doug, It seems as though your only response is to make carbon more expensive. The point about PV systems is not that they are cheaper now than all other forms of energy *right now*, but that their cost effectiveness is increasing exponentially quickly. This makes them a better investment *long-term* than the marginal sorts of improvements you are talking about in #83 IMO. As I have said before, nuclear power is the simplest near term solution for *large* reductions in GH emissions. These have already been used by, for example, the French. I don't really follow the example of the solar capture technology you advocate, but if I understand you correctly implementation of it requires a tax increase on carbon emissions(IOW it is currently too expensive, but when carbon is priced "correctly" this tech would be simple and easy to implement). As I have already argued, I think these sorts of tax increases will be increasingly difficult to bring forward, so I recommend other options. As to why the different options will be funded, this is not so terribly difficult to understand. I am pretty sure that most industrial countries actively impede the construction of nuclear power plants, we could move to a lower carbon footprint with just a shift in priorities (see the French example). As for why PV will be funded, again it comes back to the exponential nature of the growth. When PV finally becomes truly economical whoever has invested in the winning version will become absurdly, disgustingly wealthy (similar to folks who bought IBM in the 50s or Microsoft in the early 80s). You can hardly go a full week these days without some new piece of research or product that increases the efficiency or decreases the cost of solar power. Government investment in research can only speed that along. IMO, you continue to argue for a false choice where there is no way to make any progress on the GH gas front without what you might call pricing carbon accurately. There are clear alternatives that do not require this, and that would work. Cheers, :)
    0 0
  36. Shawnhet, the reason why PV systems and the like are "unaffordable" is the same reason why, for any country with substantial access to coal and the willingness to burn it, nuclear also is unaffordable, at least in the eyes of the economist's "rational man" and his present inability or unwillingness to integrate external costs of fossil fuel consumption into his equations. The capital cost of coal generation plant commissioning is substantially less than that of nuclear, somewhere in the neighborhood of half as much. And of course that's the estimate for "overnight" building costs, the perfect world. Folks like to ascribe the cost intensive nature of nuclear plant construction to excessive regulations, but I would caution anybody expecting to winnow down the overnight capital cost of a nuclear plant by eliminating regulations, operating rules and the like to think again. It's too easy to condemn construction standards and inspections without taking into a account the reason for each and every iota of regulation; there's not as much fat in nuclear regulation as we might imagine from popular literature. I've got nothing particular against nuclear power; clearly in certain contexts it works. My point in singling out nuclear plants is simply to help avoid making the mistake of imagining investors will flock to nuclear plants if given half the chance. Where are those investors today? Putting the money where they get faster ROI, such as coal plants. Why? At least in part because we're not doing full cost accounting for using coal and other fossil fuels for electrical generation. So, whatever are our pipe dreams of future energy supply, as long as there's plentiful coal and an incomplete accounting structure the private sector will have a strong preference for building coal generation plants and will continue to ignore the entire spectrum of seemingly more expensive systems.
    0 0
  37. Doug, you seem to think that nuclear power can only be funded privately, in which case you might be right about them being more expensive. However, my point was that rather than spending untold amount of effort to try and make carbon forms of energy more expensive, we can just get our governments to build them directly or to make them profitable through subsidy. This will be **way** easier than what you advocate IMO. Do you think it would be easier to make your neighbor pay for flooding your yard with waste or to pay for a (government funded) common sewer system? Isn't that very ease of application the fundamental reason why sewer systems are common and the "correct" pricing of waste is not? If someone based their whole approach to dealing with waste based on forcing people to correctly price it, wouldn't we say that they were ignoring a much simpler and more effective solution? Regardless of whether PV "should" be more economical now, it will especially if research is funded on it) become much more economical in the future, at some point making more economic sense even than untaxed carbon energy. This is what makes it a pretty good investment *even if there is no government assistance for them*. Cheers, :)
    0 0
  38. Shawnhet, the absolute price per KW of generation capacity does not vary according to who pays for it. How about if we pay for subsidies of better generation technology via revenues generated by a carbon tax? A subsidy is after all the output end of a tax, yes? Saying bye-bye to our hydrocarbon slaves is going to cost money, money we can actually see as opposed to the hidden cost of C02 emissions, a sum we're borrowing and simultaneously pretending does not exist. Call it a mitigation fee, a tax, a subsidy, whatever, the cost of C02 has to be brought into our accounting system or we're going to need an entirely new and different kind of "market magic" to make substantial progress with updating our generation systems, the kind of magic that comes from the end of a wand and suffers from lack of existence.
    0 0
  39. And how much of a no-brainer is ending any kind of subsidy on any industry that is a CO2 emitter? I am well aware that this will result in unemployed coal miners, etc - deal fairly to them by all means but their jobs are not a reason for messing the planet.
    0 0
  40. Doug, you seem to be pretty confused on this issue, so I'm not sure that there is much more I can add, I will just recap the points here as I see them. #1.You've been arguing that it is impossible to deal with this issue without properly accounting for (what you feel is) carbon's cost. However, this is clearly not the case. Have the French accurately accounted for the cost of carbon? Probably not, from your POV, but that doesn't stop them from emitting much less carbon by using nuclear technology. Again, you are acting like a crazy guy here who thinks he must properly account for the cost of his neighbor's waste instead of arguing for the construction of a sewer system. Personally, I have no idea what the "correct" cost of a month's waste dumped in my yard might be, but since I live in an area with sewers, it is not really necessary for me to know that. #2. You seem to misunderstand the scale of the supposed problem here. The fact is, that if catastrophe is looming, CO2 would have to be substantially reduced, not merely held flat. Even if everyone adopted the exact same approach as the best of the European countries, that would still be nowhere near close enough. #3.As time goes by, conservation efforts of one sort or another will get less and less efficient, in the absence of radical technological change. #4. OTOH, technological change will enable much more efficient conservation as time goes on. If current trends continue, solar power will equal fossil fuel's cost effectiveness(even at today's rates) in somewhere btw 20-40 years. Presumably, once this happens, we won't need to figure out what the correct cost of carbon-based energy, as everyone will more or less automatically switch to solar. Cheers, :)
    0 0
  41. Shawnhet, I think I'm correct when I say that the only place we've seen nuclear power adopted on a substantial scale sufficient to largely displace other means of generation is (as you point out) France, where it was made possible by massive public expenditure, via taxation. Elsewhere than France, the same technology is available and would be installed if the market deemed it financially attractive. It does not; if the market found nuclear power acceptable, we'd see it more widely deployed. I fully agree with you that C02 emissions will have to be substantially reduced in order to fix our problem. In fact, I'm not sure where we fully disagree (perhaps we're similarly crazed?) except with regard to your original incorrect assertion that the EU was increasing its GHG emissions despite government intervention of the type and scale you find attractive in France. Is it crazy to collaborate with my neighbor to rectify damage my neighbor and I are inflicting on one another by ignoring environmental costs? Is assigning a cost to our effluent (sewer tax, CCF charge, whatever) and then disposing of sewage using funds recovered from that cost assignment so crazy? I don't know, maybe you should ask your utility or other governmental entity if they believe they and you are crazy? Without some incentive of one form or another we'll burn every scrap of coal we have, until doing so becomes expensive on par with the next most expensive substitute. This in not some kind of controversial hypothesis, it's exactly what's happening today. Wishing the market away with hypothetical and especially unfunded and thus unbuilt technological fixes won't work. Cash incentives will. As long as coal is burned because we choose to ignore the costs doing so inflicts on us, no wishful thinking is going to solve this problem. So tell me, how are you going to get an investor to pay twice as much for a nuclear plant as he would for a coal plant? How are you going to persuade tax-averse Americans to pay twice as much for their generation capacity using tax dollars, and where will those tax dollars come from? In fact, the money for replacement generation plant is going to have to be extracted from somebody, us ultimately, and if that can be done in the form of a levy that simultaneously places a powerful incentive on ditching C02 emissions, so much the better.
    0 0
  42. Here's an example of what I'm babbling about incoherently in my crazy way w/regard to carbon pricing. A struggling private enterprise known as "Google" is also managed by crazy persons: Google wants a price on carbon and wants it now -- both for lofty reasons like combating global warming, but also because it could be good for business. As the Senate inches closer to climate legislation that could give the Internet giant what it wants, I checked in with Dan Reicher, the director of climate change and energy initiatives at Google to see what surfing the web had to do with reining in greenhouse gases. Turns out, the answer is technology. Reicher -- a former Department of Energy assistant secretary who now directs Google's investments in clean energy -- believes that exposing the hidden costs of dirty fuels will set off a rush of investment in new energy innovations. He says carbon pricing is an "essential signal we have to get to." Right now, "money is sitting there to make significant investments," he says, but the cash flow is sidelined because the incentives aren't there. Google climate change chief wants price on carbon
    0 0
  43. Guys, it is nice discussion but you forget the original article: the point is that any pricing of carbon emissions will create "game theoretical traps" like the tragedies of the commons. Google can want whatever they can imagine (e.g. a have seen a calculation of how much CO2 emission is caused by a google search so thjey will probalbly warmly welcome a tax on internet searches) the traps are there and waiting. Any measure that does not calculate with these traps and just wishes they were not there is bound to fail - like Kyoto.
    0 0
  44. embb (...) any pricing of carbon emissions will create "game theoretical traps" like the tragedies of the commons. Arguing that the decision whether to pay the tax or not poses a dilemma is not obvious. For example, if you import a car from China you can estimate the amount of CO2 emitted to build it using coal. If the producer denies using coal you let them carry the burden of proof because laws in your country prevents import of goods whose production damages the environment. Just because a new technology is expensive to acquire is no argument against using it if the total lifetime cost, on a global scale, is less. Any measure that does not calculate with these traps and just wishes they were not there is bound to fail - like Kyoto. Kyoto obviously failed because the Bush administration did not ratify it i.e. they defected. This perpetuated the tragedy of the commons, and several lawsuits in the US are now based on it. An interesting example is that the lawyers that faced off during the battle between 13 states and Phillip Morris in 1998, which lead to a whopping 200 billion USD settlement, have teamed up. They represent the village Kivalina and are accusing American Electric Power, BP America, Chevron, ConocoPhillips, Duke Energy, ExxonMobil, Peabody Energy, and Southern Company of conspiring to cover up the threat of man-made climate change. It is an interesting read: "A government memo obtained by Greenpeace outlines a State Department official’s talking points for a meeting with energy-company lobbyists: the president, the memo says, “rejected Kyoto, in part, based on input from you.”" That is indeed a trap that the energy companies set up for themselves.
    0 0
  45. Jacob:"Arguing that the decision whether to pay the tax or not poses a dilemma is not obvious. For example, if you import a car from China you can estimate the amount of CO2 emitted to build it using coal. If the producer denies using coal you let them carry the burden of proof because laws in your country prevents import of goods whose production damages the environment." This is in effect a trade war under the pretext of global warming - and an extreme form of protectionism. Not to mention that it does not work in practice - as it will boil down to the question of what kind of proofs will you accept? How much of a price increase are you willing to load on your own citizens - i.e. cheap imported car vs. expensive native one? How about smuggling and directly financing the mafia... Jacob:Kyoto obviously failed because the Bush administration did not ratify it i.e. they defected. No, Kyoto failed because the signatories did not implement the measures that were needed to actually achieve its goals, meaning that everybody defected - which was the logical thing to do. Lawsuits will not change that. And BTW Kopenhagen failed because the Chinese were not willing to play ball? And now several lawsuits IN CHINA are based on that???
    0 0
  46. Comparing the carbon tax with the decision to play or not to pay taxes has a pretty large logical hole: namely you have a state that has the power to make this decisin a no-brainer and it also offers benefits to those who pay their taxes in the form of schools etc. Carbon taxes do not play inside a state - so there is no police to enforce conformance - and the benefits are theoretical at most : the avoidance of something possibly bad happening in about 100 years. So all incentives are for defecting and there is no punishment - how practical is this idea?
    0 0
  47. embb This is in effect a trade war under the pretext of global warming - and an extreme form of protectionism. It could also be called scientifically founded coercion. Not to mention that it does not work in practice - as it will boil down to the question of what kind of proofs will you accept? Industry standards are already extensively used, so adding CO2-emissions is not hard. How much of a price increase are you willing to load on your own citizens - i.e. cheap imported car vs. expensive native one? The enlightened choice is between a cheap imported car that pollutes the environment and one that does not. If both cars fulfill the standards the market will pick the winner. How about smuggling and directly financing the mafia... Organized crime is a minor part of the commodities economy. Kyoto failed because the signatories did not implement the measures that were needed to actually achieve its goals, meaning that everybody defected - which was the logical thing to do. Lawsuits will not change that. No, Bill Clinton signed immidiately in 1997, but the Senate did not ratify. Bush did not sign because of lobbyism. The lawsuits then targets the lobbyism. And BTW Kopenhagen failed because the Chinese were not willing to play ball? And now several lawsuits IN CHINA are based on that??? Which lawsuits? Carbon taxes do not play inside a state - so there is no police to enforce conformance - and the benefits are theoretical at most : the avoidance of something possibly bad happening in about 100 years. That is just arguing for defection by exploiting the commons. That is why we consider strategies such as tit-for-tat, indirect reciprocity etc. You should read Hardin's and Axelrod's papers. So all incentives are for defecting and there is no punishment - how practical is this idea? The incentive is to conserve the environment, the punishment is the tax (with sanctions upon default). It seems much more practical than dealing with a ruined environment and fighting wars.
    0 0
  48. DOug, if you want to lump all the incentives into the same bag, you're going to continue to miss what I'm talking about. If we wanted to, we could, in theory, say that all generation of electricity by coal plants was illegal, right? Thus, we would not need to accurately cost carbon. This is not much different from how public sewers are funded, everyone has to contribute to the public sewer system, whether they want to or not. "Is it crazy to collaborate with my neighbor to rectify damage my neighbor and I are inflicting on one another by ignoring environmental costs? Is assigning a cost to our effluent (sewer tax, CCF charge, whatever) and then disposing of sewage using funds recovered from that cost assignment so crazy? I don't know, maybe you should ask your utility or other governmental entity if they believe they and you are crazy?" The difference here is that cost of sewage charged by your sewer utility is derived from the amount it costs to run your sewer utility, not some abstract idea on the cost of human waste. It is not based on assigning a correct value of the cost of your sewage. No one goes and lists specifically all the externalities from human waste and sets out to choose a price that reflects those externalities. They say, OTOH, that anyone who lives in location pays $x for y gallons of water or some such. The reason why this approach is common and an approach based on the true cost of human waste is common is not is practicality. Cheers, :)
    0 0
  49. Jacob:it could also be called scientifically founded coercion. You are right, it could. Wouldn`t change a thing, though. Jacob: Industry standards are already extensively used, so adding CO2-emissions is not hard. Right again! All you need is to be able to take an imported car and by measuring IT calculate how much CO2 was emitted during its manufacturing process. Easy! Jacob:The enlightened choice is between a cheap imported car that pollutes the environment and one that does not. No, it is not. The enlightened choice is between a car that possibly polluted the environment during the manufacturing and one that did not. Secondly, are you relying on the consumers enlightened choices here? Pious wish. Jacob: Organized crime is a minor part of the commodities economy. Dream on... The mafia never did anything of the alcohol interdiction in the US either. They never recognize a business opportunity... They are in fact nice guys... and WILL make the enlightened choices... BTW a report last year said that as much as 90% of the carbon credit market in the EU could be in the hands of the organized crime. Jacob:o, Bill Clinton signed immidiately in 1997, but the Senate did not ratify. I am talking about how Kyoto failed in the states that SIGNED it. never mind the US - it is a convenient target as a democratic state but the failure of the others is what we should discuss here. Jacob:Which lawsuits? Exactly! Are there any? Or are the activists looking for a cosy little armchair affair only? Jacob: That is why we consider strategies such as tit-for-tat, indirect reciprocity etc. LOL. Tit for tat would mean that if you emit co2 I will emit co2. Obviously a recipe for success. Indirect reciprocity is a different word for blackmail in this case, I guess. Jacob: The incentive is to conserve the environment, the punishment is the tax (with sanctions upon default). I But WHO wil do the punishing, pray? That is the question. Jacob:It seems much more practical than dealing with a ruined environment and fighting wars. Punishment being...?
    0 0
  50. embb I have already previously kindly answered most of your questions. Jacob:it could also be called scientifically founded coercion. You are right, it could. Wouldn`t change a thing, though. There is nothing remotely trade war-like about a scientifically founded carbon tax and coordinated import restrictions. Otherwise e.g. phthalates in plastictoys by Mattel in China would never have been removed by laws and trade restriction measures. The mafia never did anything of the alcohol interdiction in the US either. They never recognize a business opportunity. The nightmarish problem with the mafia is mostly the violence. Everybody knows that. BTW a report last year said that as much as 90% of the carbon credit market in the EU could be in the hands of the organized crime. I highly doubt that. I am talking about how Kyoto failed in the states that SIGNED it. never mind the US - it is a convenient target as a democratic state but the failure of the others is what we should discuss here. It would make no sense to disregard the defection of the largest economy. In fact, it underlines the importance of understanding the inherent dilemma of reaching and executing agreements such as this. Tit for tat would mean that if you emit co2 I will emit co2. Obviously a recipe for success. Indirect reciprocity is a different word for blackmail in this case, I guess. You seem unaware that tit-for-tat beats defection on payoff. I can also recommend actually reading the papers I provided in the post. Indirect reciprocity has nothing whatsoever to do with blackmail. P.S. Remember the comments policy of the site.
    0 0

Prev  1  2  3  Next

You need to be logged in to post a comment. Login via the left margin or if you're new, register here.


The Consensus Project Website

THE ESCALATOR

(free to republish)


© Copyright 2024 John Cook
Home | Translations | About Us | Privacy | Contact Us