The anthropogenic global warming rate: Is it steady for the last 100 years? Part 2.
Posted on 7 May 2013 by KK Tung
This is part 2 of a guest post by KK Tung, who requested the opportunity to respond to the SkS post Tung and Zhou circularly blame ~40% of global warming on regional warming by Dumb Scientist (DS).
In this second post I will review the ideas on the Atlantic Multidecadal Oscillation (AMO). I will peripherally address some criticisms by Dumb Scientist (DS) on a recent paper (Tung and Zhou [2013] ). In my first post, I discussed the uncertainty regarding the net anthropogenic forcing due to anthropogenic aerosols, and why there is no obvious reason to expect the anthropogenic warming response to follow the rapidly increasing greenhouse gas concentration or heating, as DS seemed to suggest.
For over thirty years, researchers have noted a multidecadal variation in both the North Atlantic sea-surface temperature and the global mean temperature. The variation has the appearance of an oscillation with a period of 50-80 years, judging by the global temperature record available since 1850. This variation is on top of a steadily increasing temperature trend that most scientists would attribute to anthropogenic forcing by the increase in the greenhouse gases. This was pointed out by a number of scientists, notably by Wu et al. [2011] . They showed, using the novel method of Ensemble Empirical Mode Decomposition (Wu and Huang [2009 ]; Huang et al. [1998] ), that there exists, in the 150-year global mean surface temperature record, a multidecadal oscillation. With an estimated period of 65 years, 2.5 cycles of such an oscillation was found in that global record (Figure 1, top panel). They further argued that it is related to the Atlantic Multi-decadal Oscillation (AMO) (with spatial structure shown in Figure 1, bottom panel).
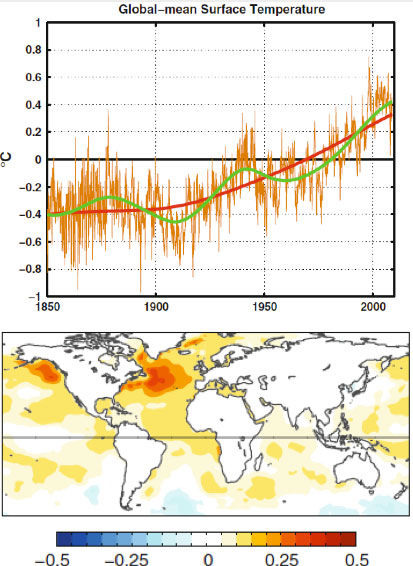
Figure 1. Taken from Wu et al. [2011] . Top panel: Raw global surface temperature in brown. The secular trend in red. The low-frequency portion of the data constructed using the secular trend plus the gravest multi-decadal variability, in green. Bottom panel: the global sea-surface temperature regressed onto the gravest multi-decadal mode.
Less certain is whether the multidecadal oscillation is also anthropogenically forced or is a part of natural oscillation that existed even before the current industrial period.
It is now known that the AMO exists in coupled atmosphere-ocean models without anthropogenic forcing (i.e. in “control runs”, in the jargon of the modeling community). It is found, for example in a version of the GFDL model at Princeton, and the Max Planck model in Germany. Both have the oscillation of the right period. In the models that participated in IPCC’s Fourth Assessment Report (AR4), no particular attempt was given to initialize the model’s oceans so that the modeled AMO would have the right phase with respect to the observed AMO. Some of the models furthermore have too short a period (~20-30 years) in their multidecadal variability for reasons that are not yet understood. So when different runs were averaged in an ensemble mean, the AMO-like internal variability is either removed or greatly reduced. In an innovative study, DelSol et al. [2011] extract the spatial pattern of the dominant internal variability mode in the AR4 models. That pattern (Figure 2, top panel) resembles the observed AMO, with warming centered in the North Atlantic but also spreading to the Pacific and generally over the Northern Hemisphere (Delworth and Mann [2000] ).
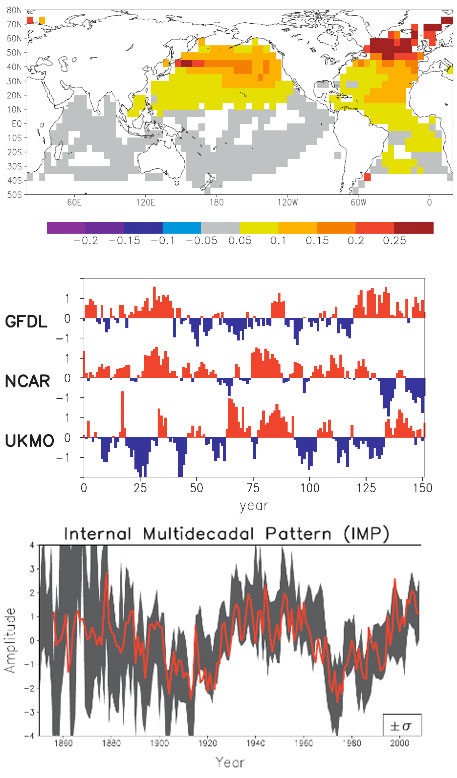
Figure 2. Taken from DelSol et al. [2011] . Top panel: the spatial pattern that maximizes the average predictability time of sea-surface temperature in 14 climate models run with fixed forcing (i.e. “control runs”). Middle panel: the time series of this component in three representative control runs. Bottom panel: time series obtained by projecting the observed data onto the model spatial pattern from the top panel. The red curve in the bottom panel is the annual average AMO index after scaling.
When the observed temperature is projected onto this model spatial pattern, the time series (in Figure 2 bottom panel) varies like the AMO Index (Enfield et al. [2001] ), even though individual models do not necessarily have an oscillation that behaves exactly like the AMO Index (Figure 2, middle panel).
There is currently an active debate among scientists on whether the observed AMO is anthropogenically forced. Supporting one side of the debate is the model, HadGEM-ES2, which managed to produce an AMO-like oscillation by forcing it with time-varying anthropogenic aerosols. The HadGEM-ES2 result is the subject of a recent paper by Booth et al. [2012] in Nature entitled “Aerosols implicated as a prime driver of twentieth-century North Atlantic climate variability”. The newly incorporated indirect aerosol effects from a time-varying aerosol forcing are apparently responsible for driving the multi-decadal variability in the model ensemble-mean global mean temperature variation. Chiang et al. [2013] pointed out that this model is an outlier among the CMIP5 models. Zhang et al. [2013] showed evidence that the indirect aerosol effects in HadGEM-ES2 have been overestimated. More importantly, while this model has succeeded in simulating the time behavior of the global-mean sea surface temperature variation in the 20th century, the patterns of temperature in the subsurface ocean and in other ocean basins are seen to be inconsistent with the observation. There is a very nice blog by Isaac Held of Princeton, one of the most respected climate scientists, on the AMO debate here. Held further pointed out the observed correlation between the North Atlantic subpolar temperature and salinity which was not simulated with the forced model: “The temperature-salinity correlations point towards there being a substantial internal component to the observations. These Atlantic temperature variations affect the evolution of Northern hemisphere and even global means (e.g., Zhang et al 2007). So there is danger in overfitting the latter with the forced signal only.”
The AMOC and the AMO
The salinity-temperature co-variation that Isaac Held mentioned concerns a property of the Atlantic Meridional Overturning Circulation (AMOC) that is thought to be responsible for the AMO variation at the ocean surface. This Great Heat Conveyor Belt connects the North Atlantic and South Atlantic (and other ocean basins as well), and between the warm surface water and the cold deep water. The deep water upwells in the South Atlantic, probably due to the wind stress there (Wunsch [1998] ). The upwelled cold water is transported near the surface to the equator and then towards to the North Atlantic all the way to the Arctic Ocean, warmed along the way by the absorption of solar heating. Due to evaporation the warmed water from the tropics is high in salt content. (So at the subpolar latitudes of the North Atlantic, the salinity of the water could serve as a marker of where the water comes from, if the temperature AMO is due to the variations in the advective transport of the AMOC. This behavior is absent if the warm water is instead forced by a basin wide radiative heating in the North Atlantic.) The denser water sinks in the Arctic due to its high salt content. In addition, through its interaction with the cold atmosphere in the Arctic, it becomes colder, which is also denser. There are regions in the Arctic where this denser water sinks and becomes the source of the deep water, which then flows south. (Due to the bottom topography in the Pacific Arctic most of the deep water flows into the Atlantic.) The Sun is the source of energy that drives the heat conveyor belt. Most of the solar energy penetrates to the surface in the tropics, but due to the high water-vapor content in the tropical atmosphere it is opaque to the back radiation in the infrared. The heat cannot be radiated away to space locally and has to be transported to the high latitudes, where the water vapor content in the atmosphere is low and it is there that the transported heat is radiated to space.
In the North Atlantic Arctic, some of the energy from the conveyor belt is used to melt ice. In the warm phase of the AMO, more ice is melted. The fresh water from melting ice lowers the density of the sinking water slightly, and has a tendency to slow the AMOC slightly after a lag of a couple decades, due to the great inertia of that thermohaline circulation. A slower AMOC would mean less transport of the tropical warm water at the surface. This then leads to the cold phase of the AMO. A colder AMO would mean more ice formation in the Arctic and less fresh water. The denser water sinks more, and sows the seed for the next warm phase of the AMO. This picture is my simplified interpretation of the paper by Dima and Lohmann [2007] and others. The science is probably not yet settled. One can see that the physics is more complicated than the simple concept of conserved energy being moved around, alluded to by DS. The Sun is the driver for the AMOC thermohaline convection, and the AMO can be viewed as instability of the AMOC (limit cycle instability in the jargon of dynamical systems as applied to simple models of the AMOC).
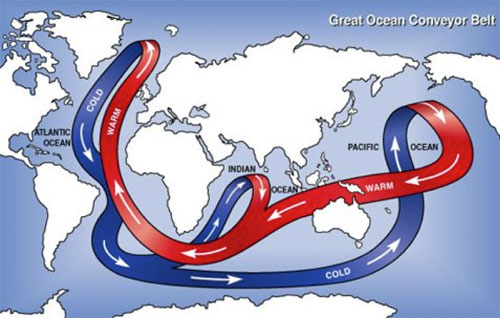
Figure 3. The great ocean conveyor belt. Schematic figure taken from Wikipedia.
Preindustrial AMO
It is fair to conclude that no CMIP3 or CMIP5 models have successfully simulated the observed multidecadal variability in the 20th century using forced response. While this fact by itself does not rule out the possibility of an AMO forced by anthropogenic forcing, it is not “unphysical” to examine the other possibility, that the AMO could be an internal variability of our climate system. Seeing it in models without anthropogenic forcing is one evidence. Seeing it in data before the industrial period is another important piece of evidence in support of it being a natural variability. These have been discussed in our PNAS paper. Figure 4 below is an updated version (to include the year 2012) of a figure in that paper. It shows this oscillation extending back as far as our instrumental and multi-proxy data can go, to 1659. Since this oscillation exists in the pre-industrial period, before anthropogenic forcing becomes important, it plausibly argues against it being anthropogenically forced.
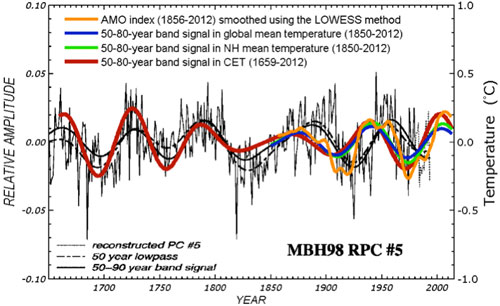
Figure 4. Comparison of the AMO mode in Central England Temperature (CET) (red) and in global mean (HadCRUT4) (blue), obtained from Wavelet analysis, with the multi-proxy AMO of Delworth and Mann [2000] (in thin black line). The amplitude of multi-proxy data is only relative (left axis). The orange curve is a smoothed version of the AMO index originally available in monthly form.
The uncertainties related to this result are many, and these were discussed in the paper but worth highlighting here. One, there is no global instrumental data before 1850. Coincidentally, 1850 is considered the beginning of the industrial period (the Second Industrial Revolution, when steam engines spewing out CO2 from coal burning were used). So pre-industrial data necessarily need to come from nontraditional sources, and they all have problems of one sort of the other. But they are all we have if we want to have a glimpse of climate variations before 1850. The thermometer record collected at Central England (CET) is the longest such record available. It cannot be much longer because sealed liquid thermometers were only invented a few years earlier. It is however a regional record and does not necessarily represent the mean temperature in the Northern Hemisphere. This is the same problem facing researchers who try to infer global climate variations using ice-core data in the Antarctica. The practice has been to divide the low-frequency portion of that polar data by a scaling factor, usually 2, and use that to represent the global climate. While there has been some research on why the low-frequency portion of the time series should represent a larger area mean, no definitive proof has been reached, and more research needs to be done. We know that if we look at the year-to-year variations in winters of England, one year could be cold due to a higher frequency of local blocking events, while the rest of Europe may not be similarly cold. However, if England is cold for 50 years, say, we know intuitively that it must have involved a larger scale cooling pattern, probably hemispherically wide. That is, England’s temperature may be reflecting a climate change. We tried to demonstrate this by comparing low passed CET data and global mean data, and showed that they agree to within a scaling factor slightly larger than one. England has been warming in the recent century, as in the global mean. It even has the same ups and downs that are in the hemispheric mean and global mean temperature (see Figure 4).
In the pre-industrial era, the comparison used in Figure 4 was with the multiproxy data of Delworth and Mann [2000]. These were collected over geographically distributed sites over the Northern Hemisphere, and some, but very few, in the Southern Hemisphere. They show the same AMO-like behavior as in CET. CET serves as the bridge that connects preindustrial proxy data with the global instrumental data available in the industrial era. The continuity of CET data also provides a calibration of the global AMO amplitude in the pre-industrial era once it is calibrated against the global data in the industrial period. The evidence is not perfect, but is probably the best we can come up with at this time. Some people are convinced by it and some are not, but the arguments definitely were not circular.
How to detrend the AMO Index
The mathematical issues on how best to detrend a time series were discussed in the paper by Wu et al. [2007] in PNAS. The common practice has been to fit a linear trend to the time series by least squares, and then remove that trend. This is how most climate indices are defined. Examples are QBO, ENSO, solar cycle etc. In particular, similar to the common AMO index, the Nino3.4 index is defined as the mean SST in the equatorial Pacific (the Nino3.4 region) linearly detrended. Another approach uses leading EOF in the detrended data for the purpose of getting the signal with the most variance. An example is the PDO. One can get more sophisticated and adaptively extract and then subtract a nonlinear secular trend using the method of EMD discussed in that paper. Either way you get almost the same AMO time series from the North Atlantic mean temperature as the standard definition of Enfield et al. [2001] , who subtracted the linear trend in the North Atlantic mean temperature for the purpose of removing the forced component. There were concerns raised (Trenberth and Shea [2006 ]; Mann and Emanuel [2006] ) that some nonlinear forced trends still remain in the AMO Index. Enfield and Cid-Serrano [2010] showed that removing a nonlinear (quadratic) trend does not affect the multidecadal oscillation. Physical issues on how best to define the index are more complicated. Nevertheless if what you want to do is to detrend the North Atlantic time series it does not make sense to subtract from it the global-mean time variation. That is, you do not detrend time series A by subtracting from it time series B. If you do, you are introducing another signal, in this case, the global warming signal (actually the negative of the global warming signal) into the AMO index. There may be physical reasons why you may want to define such a composite index, but you have to justify that unusual definition. Trenberth and Shea [2006] did it to come up with a better predictor for a local phenomenon, the Atlantic hurricanes. An accessible discussion can be found in Wikipedia. http://en.wikipedia.org/wiki/Atlantic_multidecadal_oscillation
The amplitude of the oscillatory part of the North Atlantic mean temperature is larger than that in the global mean, but its long-term trend is smaller. So if the global mean variation is subtracted from the North Atlantic mean, the oscillation still remains at 2/3 the amplitude but a negative trend is created. K.a.r.S.t.e.N provided a figure in post 30 here. I took the liberty in reposting it below. One sees that the multidecadal oscillation is still there. But the negative trend in this AMO index causes problems with the multiple linear regression (MLR) analysis, as discussed in part 1 of my post.
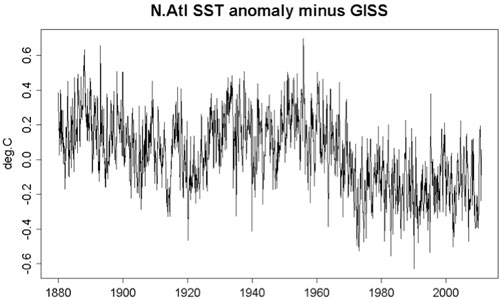
Figure 5: North Atlantic SST minus the global mean.
From a purely technical point, the collinearity introduced between this negative trend in the AMO index and the anthropogenic positive trend confuses the MLR analysis. If you insist on using it, it will give a 50-year anthropogenic trend of 0.1 degree C/decade and a 34-year anthropogenic trend of 0.125 degree C/decade. The 50-year trend is not too much larger than what we obtained previously but these numbers cannot be trusted.
One could suggest, qualitatively, that the negative trend is due to anthropogenic aerosol cooling and the ups and down due to what happens before and after the Clean Air Act etc. But these arguments are similar to the qualitative arguments that some have made about the observed temperature variations as due to solar radiation variations. To make it quantitative we need to put the suggestion into a model and check it against observation. This was done by the HadGEM-ES2 model, and we have discussed above why it has aspects that are inconsistent with observation.
The question of whether one should use the AMO Index as defined by Enfield et al. [2001] or by Trenberth and Shea [2006] was discussed in detail in Enfield and Cid-Serrano [2010] , who argued against the latter index as “throwing the baby out with the bath water”. In effect this is a claim of circular argument. They claimed that this procedure is valid “only if it is known a priori that the Atlantic contribution to the global SST signal is entirely anthropogenic, which of course is not known”. Charges of circular argument have been leveled at those adopting either AMO index in the past, and DumbScientist was not the first. In my opinion, the argument should be a physical one and one based on observational evidence. An argument based on one definition of the index being self-evidently correct is bound to be circular in itself. Physical justification of AMO being mostly natural or anthropogenically forced needs to precede the choice of the index. This was what we did in our PNAS paper.
Enfield and Cid-Serrano [2010] also examined the issue of causality and the previous claim by Elsner [2006] that the global mean temperature multidecadal variation leads the AMO. They found that the confusion was caused by the fact that Elsner used a 1-year lag to annualized data: While the ocean (AMO) might require upwards of a year to adjust to the atmosphere, the atmosphere responds to the ocean in less than a season, essentially undetectable with a 1-year lag. The Granger test with annual data will fail to show the lag of the atmosphere, thus showing the global temperature to be causal.
What is an appropriate regressor/predictor?
There is a concern that the AMO index used in our multiple regression analysis is a temperature response rather than a forcing index. Ideally, all predictors in the analysis should be external forcings, but compromises are routinely made to account for internal variability. The solar forcing index is the solar irradiance measured outside the terrestrial climate system, and so is a suitable predictor. Carbon dioxide forcing is external to the climate system as humans extract fossil fuel and burn it to release the carbon. Volcanic aerosols are released from deep inside the earth into the atmosphere. In the last two examples, the forcing should actually be internal to the terrestrial system, but is considered external to the atmosphere-ocean climate system in a compromise. Further compromise is made in the ENSO “forcing”. ENSO is an internal oscillation of the equatorial Pacific-atmosphere system, but is usually treated as a “forcing” to the global climate system in a compromise. A commonly used ENSO index, the Nino3.4 index, is the mean temperature in a part of the equatorial Pacific that has a strong ENSO variation. It is not too different than the Multivariate ENSO Index used by Foster and Rahmstorf [2011] . It is in principle better to use an index that is not temperature, and so the Southern Oscillation Index (SOI), which is the pressure difference between Tahiti and Darwin, is sometimes used as a predictor for the ENSO temperature response. However, strictly speaking, the SOI is not a predictor of ENSO, but a part of the coupled atmosphere-ocean response that is the ENSO phenomenon. In practice it does not matter much which ENSO index is used because their time series behave similarly. It is in the same spirit that the AMO index, which is a mean of the detrended North Atlantic temperature, is used to predict the global temperature change. It is one step removed from the global mean temperature being analyzed. A better predictor should be the strength of the AMOC, whose variation is thought to be responsible for the AMO. However, measurements deep ocean circulation strength had not been available. Recently Zhang et al. [2011] found that the North Brazil Current (NBC) strength, measured off the coast of Brazil, could be a proxy for the AMOC, and they verified it with a 700-year model run. We could have used NBC as our predictor for the AMO, but that time series is available only for the past 50 years, not long enough for our purpose. They however also found that the NBC variation is coherent with the AMO index. So for our analysis for the past 160 years, we used the AMO index. This is not perfect, but I hope the readers will understand the practical choices being made.
References
Booth, B. B. B., N. J. Dunstone, P. R. Halloran, T. Andrews, and N. Bellouin, 2012: Aerosols implicated as a prime dirver of twentieth-century North Atlantic climate variability. Nature, 484, 228-232.
Chiang, J. C. H., C. Y. Chang, and M. F. Wehner, 2013: Long-term behavior of the Atlantic interhemispheric SST gradient in the CMIP5 historial simulations. J. Climate, submitted.
DelSol, T., M. K. Tippett, and J. Shukla, 2011: A significant component of unforced multidecadal variability in the recent acceleration of global warming. J. Climate, 24, 909-026.
Delworth, T. L. and M. E. Mann, 2000: Observed and simulated multidecadal variability in the Northern Hemisphere. Clim. Dyn., 16, 661-676.
Elsner, J. B., 2006: Evidence in support of the climatic change-Atlantic hurricane hypothesis. Geophys. Research. Lett., 33, doi:10.1029/2006GL026869.
Enfield, D. B. and L. Cid-Serrano, 2010: secular and multidecadal warmings in the North Atlantic and their relationships with major hurricane activity. Int. J. Climatol., 30, 174-184.
Enfield, D. B., A. M. Mestas-Nunez, and P. J. Trimble, 2001: The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental U. S. Geophys. Research. Lett., 28, 2077-2080.
Foster, G. and S. Rahmstorf, 2011: Global temperature evolution 1979-2010. Environmental Research Letters, 6, 1-8.
Huang, N. E., Z. Shen, S. R. Long, M. L. C. Wu, H. H. Shih, Q. N. Zheng, N. C. Yen, C. C. Tung, and H. H. Liu, 1998: The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London Ser. A-Math. Phys. Eng. Sci., 454, 903-995.
Mann, M. E. and K. Emanuel, 2006: Atlantic hurricane trends linked to climate change. Eos, 87, 233-244.
Trenberth, K. E. and D. J. Shea, 2006: Atlantic hurricanes and natural variability in 2005. Geophys. Research. Lett., 33, doi:10.1029/2006GL026894.
Tung, K. K. and J. Zhou, 2013: Using Data to Attribute Episodes of Warming and Cooling in Instrumental Record. Proc. Natl. Acad. Sci., USA, 110.
Wu, Z. and N. E. Huang, 2009: Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv. Adapt. Data Anal., 1, 1-14.
Wu, Z., N. E. Huang, S. R. Long, and C. K. Peng, 2007: On the trend, detrending and variability of nonlinear and non-stationary time series. Proc. Natl. Acad. Sci., USA, 104, 14889-14894.
Wu, Z., N. E. Huang, J. M. Wallace, B. Smoliak, and X. Chen, 2011: On the time-varying trend in global-mean surface temperature. Clim. Dyn.
Wunsch, C., 1998: The work done by the wind on the oceanic general circulation. J. Phys. Oceanography, 28, 2332-2340.
Zhang, D., R. Msadeck, M. J. McPhaden, and T. Delworth, 2011: Multidecadal variability of the North Brazil Current and its connection to the Atlantic meridional overtuning circulation. J. Geophys. Res.,, 116, doi:10.1029/2010JC006812.
Zhang, R., T. Delworth, R. Sutton, D. L. R. Hodson, K. W. Dixon, I. M. H. Held, Y., J. Marshall, Y. Ming, R. Msadeck, J. Robson, A. J. Rosati, M. Ting, and G. A. Vecchi, 2013: Have aerosols caused the observed Atlantic Multidecadal Variability? J. Atmos. Sci., 70, doi:10.1175/JAS-D-12-0331.1.































 Arguments
Arguments






























Dr Tung writes: "That model spread is rather large. If you are satisfied with that, that is fine with me."
The model spread is indeed large, the key question is whether there is a good reason to suppose that the spread should be smaller, and you so far have provided no evidence or argument to suggest that it should. Of course we want the projection to have as great a certainty as possible, so none of us are "satisfied" with the spread and why climate modelling groups are working hard to improve their models.
"And I am not sure how the models can be made to do it since we do not know the initial condition in the ocean sublayer well in 1850-1870 (the time these model simulations start)."
That is the entire point of using a Monte Carlo simulation. We can't predict chaotic phenomenon, but we can simulate them, so that is what we do and the spread of the model is an indication of what is plausible given what we know about the underlying physics.
"My comments about the CMIP3 model underpredicting the warming should not be taken as a criticism of the models"
In that case, I think you need to be more careful in how you express yourself as there are those in the public debate on climate that are likely to use your words to argue that the models are flawed. The statement however is still wrong - the models DON'T underpredict the warming, the ensemble mean IS NOT a hindcast of the observed climate change, only the forced component. The enembles hindcast of the actual climate is that it lies somewhere in the spread of the model runs, which indeed it does, so the models DO NOT underpredict the warming. I'm sorry to go on about this, but this is a fundamental point in understanding what the model ensemble actually says.
"One could take the point of view that the internal variability is just climate noise, and that the difference from any such unpredictable (by models) internal variability should be considered as "insignificant" (p595 of AR4) (post 33 here)"
It is only insignificant for the purposes of deciding whether the models do what they are intended to do correctly, which is to hindcast/project the forced component of the climate change.
"This is in essence a statement that we will ignore internal variabilities just because we have not found a way to simulate it using the current generation of models."
This is a deeply unfair and uncharitable characterisation of a community of hard working scientists. In making policy for (in)action on fossil fuel use, the key question is what is the effect of fossil fuel emissions on future climate. The answer to this question depends only on the forced component of climate change. This means the modellers are giving the direct answer to the question posed. They are not ignoring internal variabilities, far from it, the spread of the model runs is a good way of characterising the plausible effects of internal variability (according to our current understanding of the physics).
With my memories of the heavy-going I encountered discussing the more straightforward issues raised in part 1 of this post, this second part would appear a nightmare.
One of the areas I consider worthy of discussion is the reconstruction of the past AMO. Tom Curtis has already addressed some aspects of this up-thread.
The existence of an AMO prior to the industrial age would give much credence to the Tung & Zhou 2013 thesis. But I find the offered analysis, the statistical significance identified between CET & Mann et al 1998 RPC#5 data, to be less than convincing. The wavelet analysis on CET will yield a 50-80 year signal of some sort, just as the Mann et al filtering will yield a 50-90 year signal. And as there are such signals existing in synchronisation in both the AMO & the CET for the last 130 years, it would take very little for them to stay in synchrony for a further 200 years into the past. So why is this 50-80 year cycle in CET more than just a form of cherry-picking?
Mann et al 1998 is not the only extended AMO reconstruction. Gray et al 2004 present an AMO reconstruction 1567-1990 which certainly looks more convincing that Mann et al 1998 when compared to Enfield et al 2001. Gray et al 2004 was noted within Tung & Chou 2013 but not seriously considered for analysis. And Gray et al 2004 shows nothing convincing by way of a periodic AMO that could be resulting from natural variation.
For illustration, I have plotted the Enfield, Mann & Gray AMO series here.
In reply to post 51 by Dikran Marsupial:You have taken my statements on model-observation discrepancy out of context. We all seem to agree that ensemble mean model results reveal the forced response. And we all agree that this one realization that is our observed climate in principle contains internal variability as well as forced response. If model ensemble mean systematically under predicts the observed warming, as happens in the first half of the 20th century, it is legitimate for a scientist to ask whether the difference could be caused by the presence of internal variability in the real climate. To me the discrepancy is revealing and is what we should be learning from models. This is not a criticism of the models. You first claimed that the difference was insignificant because the internal variability is unpredictable by models and quoted AR4 to support your view. Then when I replied that your position was essentially asking us to ignore internal variability you accused me of being deeply unfair and uncharitable to the community of hard working scientists. I am sorry that our scientific discourse has taken this sad turn.
Dr Tung, electronic forms of communication have a tendency to be percieved (on both sides) as being more aggressive than is intended. None of what I have written is intended as an attack on you, but is intended to understand your statements and to discuss and correct errors where they appear. That is the way science should work. I find the best way to go about this is to ask direct questions and give direct answers; however when they are not answered this inevitably leads to misunderstandings.
The ensemble mean is the models estimate of the forced response, I think we can agree on that.
Now I would say that the spread of the ensmeble (at least for a particular model) characterises the plausible effects of the unforced response (i.e. natural variability) and the observations can only be expected to lie within the spread of the models runs and no closer. Do you agree with that?
Now you have said that the spread of the models is wide, and I have agreed that it is. However, what I want to know is whether you think there is good reason to expect the spread of the models to be any smaller than it is. This question is intended to help me understand why you appear to think that the models under-predict the warming. As far as I can see it doesn't, the warming lies within the stated uncertainty of the hindcast.
Essentially when comparing observations with models you need to look at BOTH the ensemble mean AND the spread of the ensemble as they are both integral parts of the projection/hindcast. If you only look at the ensemble mean and igniore the spread, you are ignoring the information about internal variability that the model provides.
I'm sorry, but in my view you are being unfair in suggesting the modellers use the ensemble mean because they can't predict chaotic phenomenon, firstly becuase the forced component is the answer to the question posed by the politicians and secondly because they don't ignore internal variability, the spread of their model ensemble is a characterisation of internal variability. If the modellers only used the ensemble mean the comment would be fair, but they don't. Do you disagree with either of these statements? If so, please can you explain why.
In reply to post 54 by Dikran Marsupial: I agree with everything you said except the last paragraph, where you still accuse me of being unfair to modelers. I am one of them and I had no intention of doing so.
What is nice about this way of communication is that what we said are all recorded. You can go back to reread what I said and see if I was being unfair. My statements were about what we could learn from the models, in particular about model-observation systematic discrepancies. We have looked at both CMIP 3 and CMIP5 model result archives, at individual model's ensemble means where it is available. What it reveals to me is a tendency for the model ensemble means to under predict the observed warming in the early half of the 20th century. I wanted to learn from this model result, while you thought I was a unfairly attacking the hard working modelers. I suggested that the discrepancy was possibly due to the absence of internal variability in the ensemble mean. The ensemble means were not supposed to contain much internal variability. We both agree with that.
The intermodel spread is an entirely different matter.
I'm sorry Dr Tung, I explained why it is important to look at the spread of the model runs as that is the way in which the models characterise internal variability. You agree with me on this point, as you wrote "I agree with everything you said except the last paragraph", yet you then follow this by "discussing model-observation systematic discrepanices", without reference to the spread of the model runs and concentrating solely on the ensemble mean.
Of course the model ensemble means don't exactly match the observations, but this is not evidence of a systematic discrepancy, it is evidence of a stochastic/chaotic discrepancy, which the spread of the models clearly tells us we should expect to see.
I will now bow out of the discussion. I have explained why I feel your comment was unfair, and explained the two reasons for this, and asked you "Do you disagree with either of these statements? If so, please can you explain why.". I am perfectly willing to change my mind if I am wrong, but if polite questions are asked that are designed to address a misunderstanding, and those questions are ignored, the chance of a productive discussion are rather slim. Note I did not mean to imply that your comments were deliberately unfair.
This has been a very interesting discussion and I would be very disappointed if an aggressive tone led to a premature conclusion. I would really encourage the participants to keep discussing the science. It's rare to see such debate online.
I find discussions like this delightful - although I find myself wanting to wave my arms as I talk, scribbling back and forth on a white-board.
I invariably learn from them, even in the (all too common, sadly) case of finding I was completely mistaken. :)
Dr. Tung:
I have been watching the disucssion, but I have been mostly staying out of it. One of the comments policies here at SkS is "no dogpiling", which means SkS does not want one participant to have to deal with comments from a large number of people at the same time. In this case, I have tended to stay out because you, as author of the blog post, may find it discouraging if you have to have multiple conversations with multiple participants at the same time. It is more constructive to keep a small number of conversations going, and avoid having you feel overwhelmed.
Nonetheless, I have been reading, and Dikran has suggested that he'll be dropping out, so I am going to pick up the conversation with one point that you have repeated several times. In #55, you said:
Now here is the problem that I have with that statement, and what I believe Dirkan has been trying to point out in his comments about the spread of the model simulations:
- you have agreed that the ensemble mean represents primarily the "forced response" (at least, better than a single model run would).
- you seem to be neglecting that the observations always represent both the forced response plus the internal variability. It cannot possibly be any other way - the observations include everything. Thus it is, in part, an apples-oranges comparison to look at observation with respect to the ensemble mean.
You cannot come to a conclusion that the ensemble mean of the models is in error (which is what "under predict" is saying) unless you can separate the forced portion of the observations from the internal variation portion. And that is exceedingly difficult.
Even in a single model run, you cannot easily separate the forced and non-forced portions of the response. However, if you run the model a number of times, with slightly different initial conditions, each different model run will have the same forced response, but a different "internal variability" response. Averaging those runs will see the forced response have the same effect on the ensemble mean (thus it will be strongly represented), but the differing internal variability between runs will tend to cancel out and not appear in the mean.
At that point, the ensemble mean no longer tells you about internal variability - but you can look at the entire range of individual model runs to see how far the internal variability can change the results from the forced response.
..and to get back to the observations - as long as the observed temperatures fall along the path that could have happened in any one of the many possible single model runs, then you have to accept that the observations are not in disagreement with what the model has done. After all, if you picked a different model run, you'd see a different combination of forced response plus internal variability - and the model isn't "wrong" until it is different from all single model runs (i.e., it falls outside th range).
In summary, I simply disagree with you that comparing the ensemble mean to the observations is an appropriate test. The ensemble mean could be a perfect match for the real forced response, and the ensemble mean and observations would still be different because the observations include both the forced response and the internal variability.
In reply to post 56 and post 59: I must have been a terrible communicator that you both think that I said the opposite of what I wanted to say on some aspects of the problem. So let me try again in a different way. Let us remove the emotions and value judgements by considering a perfect model of our climate, a hypothetical model. Because of chaos, and the hypersensitivity to the initial conditions, we can only hope to simulate the observed forced response, not the observed response which contains definitely both forced and unforced response. To reveal the model forced response, we need to average out the internal variability by ensemble averaging. We need at least 15 ensemble members, each initiated differently. Suppose we have the resources for doing them and we now have the perfect model forced response. Now we want to compare with the observed response, but we do not know what the observed forced response is. But we find the model ensemble mean to under predict the observed warming rate in the first half of the twentieth century. What can we conclude from this fact? By using the word "under predict" I can't possibly be saying the model's forced solution is in error. Remember we said the model is perfect. Is it unfair to the hardworking folks who produce this model to even compare the model with the observation and notice this systematic discrepancy? Notice that I used the word "discrepancy" and not the word "error". In this hypothetical case the discrepancy is certainly due to the presence of a multidecadal internal variability (do I dare to say the AMO?), which is present in this one realization that is our observed climate but not in the ensemble mean model result.
"In this hypothetical case the discrepancy is certainly due to the presence of a multidecadal internal variability"
Or it is due to two episodes of opposite sign of subdecadal variablility coincidentally timed.
Or possibly it is due to an incorrect characterization of the forcing agents (ie, the paleoclimatologists got it wrong, not the modellers).
Or it is due to errors in the instrumental record due to reduced coverage consequent on the two world wars.
Or it is due to synergy of two or more oceanic oscilations that do not coincide more than once every thousand years on average.
Or ....
The leap to the AMO is not justified, and is certainly not justified on the AR4 model runs which do not have a systematic error in the post 1950 temperature record which would be there if the AMO was the cause of "systematic discrepancy" in the early twentieth century. If you are to run your argument, you must at least assume the models are in error about the post 1950 forcing response, and hence presumably the pre-1950 responce. Having done that, you are not entitled to assume a "perfect" model will continue to show the pre-1950 discrepancies.
Continue with my post 60: I hope post 60 can clear up the confusion and we can get back to the scientific issue at hand.
Back to CMIP3 models. I mentioned that the intermodel spread is rather large. It is difficult to conclude anything concrete with the intermodel spread. For political reasons less developed models from some countries were included. Some models have unrealistic internal variability. I know of one model with a perfectly periodic ENSO with exactly two year period that is also quite large in amplitude. Another model with a huge decadal variability of 0.4 C in the global mean temperature. In the 40 years the early twentieth century warming also warmed by 0.4C in the observed global mean temperature. When all of the model results are averaged in the all model ensemble mean, only 0.2 C warming is found during this period. There should have enough members in the all-model ensemble mean to eliminate the model internal variability, but we are not sure if that ensemble mean gives the correct forced solution. We could pick a few models we know and trust and look at them. Although there were not enough ensemble members available (usually 5 were done), we suspect that they were good enough to reveal approximately the forced response. During the first half of the 20th century, the warming generally were rather flat in these models that we examined. This is also a period during which the AMO was in its warm phase and can contribute 0.3 C to the warming. This was my thought process. It was not intended to be a criticism, but I might have pushed one of the hot buttons for some of you unknowingly. Could it be the word "under predict", which to me just means that the model warming is less than the observed warming. I did not attach any value judgement to it.
Dr Tung,
But we find the model ensemble mean to under predict the observed warming rate in the first half of the twentieth century.
You keep making this statement as if it is self-evidently meaningful so allow me to ask a very simple question:
If you plot the observed warming rate in the first half of the 20th century together with all of the model simulations, does it stand out? In other words, can you pick out which one is the observed warming without knowing in advance which line represents the observations and which lines represent the simulations?
My answer to that question would be "No", based on Figure 9.5 (a) from AR4, posted already by KR in #23 and reproduced here for convenience:
If the observed warming wasn't black then you wouldn't be able to distinguish it from any of the individual realisations of the climate models. Contrast this with Figure 9.5 (b) above — the behaviour of the black line clearly stands out from the individual realisations in the second half of the century and is even the most extreme realisation a few times in the first half.
A more sophisticated test would be: "What is the range of trends for the individual realisations for the first half of the 20th century? Is there a statistically significant difference between the observed trend and that range?"
All of this is even before considering Tom Curtis' points, which are also valid, and the fact that Kevin C's simple 2-box model does a remarkable job of matching the observations with just the forced response and ENSO.
In reply to Tom Curtis in post 61: your points are well taken. Assume the observation is perfect in my hypothetical argument. By "multidecadal internal variability" you could take it to mean "internal variability that in this multidecadal period in total gives rise to an additional warming"
I find it frustrating that I often get bogged down by words. I was surprised by so much nitpicking that distracts the discussion into a different direction. I guess I shouldn't have been surprised. After all this is Skeptical Science.
Dr Tung,
It was not intended to be a criticism, but I might have pushed one of the hot buttons for some of you unknowingly. Could it be the word "under predict", which to me just means that the model warming is less than the observed warming. I did not attach any value judgement to it.
I think the issue is that we're used to statements like that being supported. There are many potential reasons why the models might under-predict the early 20th century warming but we'd like that to be established before moving on to the implications.
Your point about inter-model variability is a good one. One danger of combining different models with different systematic errors is that the systematic differences become part of the spread (i.e. it makes it harder to distinguish between internal variability, which is meant to model non-climactic "noise", and systematic differences between models).
If this is a genuine issue that you have identified then you should be able to answer "Yes" to my first question in my last comment — there is a test that would allow you to distinguish between the actual observations and any of the individual model realisations. If so, please present it, it would be really interesting to see.
In reply to post 63 and post 65 by JasonB: you and others are asking a different question and a different test than the point I was trying to make. The question you asked was if I claim that the model is in error in under predicting the observed warming what statistical test do I have to prove it. The standard test, which many of you are alluding to, is to test if the mean of all the ensemble members is different from the observation by seeing if it is within two standard deviations of the variance created by the ensemble members. If so then I cannot claim that the model is in error because the difference is random climate noise. My question was different, it concerns forced response vs unforced response. I used the model ensemble mean to approximate the forced response. If I see the forced response is lower than the observation, which contains both forced and unforced internal variability, I tentatively attribute the difference to internal variability that is not and should not be in the ensemble mean. It is tentative because there were not enough ensemble members from any modeling group in CMIP3. I see it happen systematically in most models we looked at with more attention paid to models we trust. I mentioned it previously as an revelation to me, a thought process that is often necessary in science, not a proof in mathematics. You may have a different thought process for discovery. I know of mathematicians who do not proceed to solve for the solution to a partial differential equation until they could prove that the existence and uniqueness of the potential solution.
Dear Prof Tung, "underpredict" and "discrepancy" are both words that carry a strong implication that two things should be the same, but aren't.
As we agree, the ensemble mean is an estimate of only the forced response. This means that it is not itself a prediction of observed temperatures. Therefore it is unfair to say that the ensemble mean underpredicts something that it does not actually attempt to predict.
The collins dictionary says this about the word "discrepancy":
"Discrepancy is sometimes wrongly used where disparity is meant. A discrepancy exists between things which ought to be the same; it can be small but is usually significant. A disparity is a large difference between measurable things such as age, rank, or wages"
Now if you had said there was a difference rather than a discrepancy, your statements would have been far less of an issue.
Note this is not nitpicking. There are many skeptical arguments used to criticise models that explicitly or implicitly are based on the assumption that the observations should lie close to the ensemble mean (which would seem reasonable to most, but which we would I hope agree is incorrect). Sometimes these arguments even make it through into publciations in peer reviewed journals, for example Douglass et al (2008). When discussing science for the general public, especially on a contentious subject, such as climate change, it is very important to make sure that ones choice of words is correct and does not propogate misunderstandings.
I offer this in the hope that we can return to the substantive issue, which is the circularity of the proposed method.
Replying to post 67 by Dikran: Your comment is well taken. I had suspected that all these accusations of my motives may be due to a word that I used. Instead of the word "underpredict" I should have used a longer phrase "a difference and the difference is negative when taken as the model ensemble mean minus the observation". I will try to be more careful commenting on this site and not use short-hand words. Often when I was busy or in a noisy environment trying to reply using my ipad I tend to write tersely, and it has not worked here.
I'm sorry Dr Tung, but there were no accusations of your motives, in fact I clearly stated "I did not mean to imply that your comments were deliberately unfair".
Busy, so not much time to comment, but I want to stress Dikran's comment in #67, and put it more bluntly:
The model ensemble mean can't be used as a prediction of forced response plus internal variability, and thus is can't "under predict". Regardless of what label you put on it, I think you are over-interpreting the difference.
Also as Dikran points out: you need to get back to the points people have raised about the circularity of the argument. I think that your repeated "under predict" type vocabulary underlies a lack of realization that that you have potentially serious issues related to your methodology. You are interpreting things in a fashion that is not supported by either the evidence or your discussion, but you don't seem to be able to step back and realize that there is an implicit assumption in your work that is not jsutified (and is leading you in the wrong direction).
...back to reader mode...
Another thought just popped in. You (Dr. Tung) said:
The problem is that "under predict" is a value judgment. Just as "discrepancy" is. A non judgmental wording would be "the numbers are not the same".
Part of my science training was the importance of making clear distinctions amongst "observations", "interpretations", and "conclusions". Not only is "under predict" not an observation, it is not even an interpretation - it is a conclusion.
And we're "nit-picky" not because we're at Skeptical Science - we're nit-picky because that is what scientists do...
In reply to post 70 and 71: I may have used the word "underpredict" and "discrepancy" incorrectly, but the meaning was clear because I elaborated many times and in different ways what I meant. It was even clear from my first mention that I was using the ensemble mean as the prediction of the forced response only. But you keep repeating an erroneous interpretation of what I said, as using the ensemble mean as a prediction of forced response plus internal variability. I never said that. In fact I kept saying the opposite. We are all wasting our time here.
Dr Tung,
We are all wasting our time here.
On the contrary, this latest exchange has definitely cleared up some confusion that I, and apparently many others, had about your position. You may feel that the meaning was clear but by continuing to use a word that carries a different meaning to that which you were apparently trying to express, it made it difficult for others to discern.
So this has certainly been productive and should move the discussion forward.
Prof. Tung, I don't think we are wasting our time either. It is unfortunate that misunderstandings ocurr sometimes, but we wouldn't be so thorough in trying to get to the bottom of them if we didn't think understanding the science properly was important.
Dr. Tung.
OK. Let's follow up on my comment in #71, and apply it to your study. I am not an expert on AMO, but from what I have read here, I would state the following:
- temperature can be classified as an observation
- pressure can be classified as an observation
- I'd even be content classifying the pressure difference between two locations as an "observation" - e.g., Southern Oscillation Index based on Tahiti-Darwin - so when it comes to linking an oscillation (ENSO) to temperatures, SOI is a methodologically-independent observation and it is appropriate to use it to try to explain temperatures.
AMO, which from descriptions here and in the NOAA link is described as a detrended areal average of temperatures, is not an observation. It is an interpretation of a rather large number of observations, and it includes processing that removes part of the signal contained in the original observations (the detrending).
Once you start using that interpretation of the data as if it is an "observation", and then attempt to use your analysis to deternine the portion of the observed temperatures that is attributable to AGW, then you are at risk of making errors. The AMO, as an interpretation, has built-in assumptions. The detrending has changed the character of the information contained in the result (as compared to the original temperature observations). The averaging and detrending are based on a statistical model, and the remaining values (the AMO) represent the parts that the model doesn't remove or smooth.
Now, if your goal is to get people to accept your conclusions, then you are going to have to go back over the steps from observation, through interpretation, to your conclusions. You are going to have to provide an analysis that clearly demonstrates that the result you want us to believe is not affected by the assumptions (especially detrending) that are inherent in the application of processing/modeling to derive the AMO.
From what I have read here and elsewhere on the web, this is a serious methodological flaw, and you have not addessed the criticisms that have been made here. Please go back over Dumb Scientist's original post, and the comments to both it and your two posts, and address the issue of the detrending that is done in deriving the AMO.
This is not quibbling about definitions of words. The distinction between "observations" and "interpretations" is essential. You are attempting to explain temperatures using temperatures, which seems unsupportable - it involves a circularity that is hidden because you appear to be forgetting that AMO is not an observation.
In reply to post 73 by Jason B and post 74 by Dikran: I accept your position. I understand that this is a necessary step for you before we can move forward. I was just becoming impatient because I was trying to make two simple points about Figure 9.5 in AR4, and then use the time available to go back to reply to some of the interesting (to me at least) comments that were posted here. I barely made the first point about that figure before being distracted.
The first point is, we can use the model ensemble mean as a proxy for the forced response in the observation. Since the observation contains both forced response and internal variability, comparing the ensemble mean from a model and the observation may tell us something about the presence of the internal variability. I saw the possibility of internal variability explaining about half of the observed early twentieth century warming. This is not a firm conclusion because afterall the models may contain systematic errors. If the models were perfect, this impression could be made into a firmer conclusion.
The second point concerns comparing Figure 9.5a with Figure 9.5b (the figure is shown in post 65 by JasonB), still assuming that the model ensemble mean serves as a proxy for the forced response in the observation. The interpretation is that in the second half of the twentieth century, CMIP3 models used by AR4 produced all the observed warming by anthropogenic forcing. Without anthropogenic forcing, Figure 9.5b shows that the all-model ensemble mean (the blue curve), has no warming or even negative warming. Figure 9.5a shows that with anthropogenic forcing, the all-model ensemble mean reproduces the observation very well (compare the blue red curve with the black curve). Since we all agreed earlier that the observation should contain internal variability as well as forced response, this is telling us that the AR4 models do not need internal variability to simulate the observation during the second half of the twentieth century.
You probably are aware of the discussions on the recent hiatus in warming for the past 17 years. A possible explanation is that that is caused by internal variability. The CMIP3 models, which do not need internal variability to explain the accelerated warming since 1980, have projections that overshoot the observation in the recent decades, beyond the 95% range. While we could still take the position that this is fine, because one can always add back internal variability when we need it to explain the difference, it becomes rather awkward to only insert an internal variability that cools for the past 17 years and not a warming internal variability during the period of accelerated warming. In any case, we do not have a coherent sense of the internal variability in the warm vs cool episodes in the observation.
@76 - "You probably are aware of the discussions on the recent hiatus in warming for the past 17 years."
I cannot say that I am.
"...the past 17 years" you say? Would that be 1996-2013? Where abouts on AR4 fig 9.5a is there such a "hiatus" evedent (bearing in mind that AR4 fig 9.5a shows "the observation ... (black curve)" to 2005 if not 2006)?
I suggested that anthropogenic forcings were faster after 1950. In response, you discussed logarithms and aerosols that were already taken into account in the IPCC radiative forcings chart I originally linked:
Then you linked to that same forcings chart and linked to another:
The estimates you linked both show that anthropogenic forcings increased faster after 1950. So do the GISS and Potsdam estimates. Perhaps all these estimates are wrong, but you can't prove them wrong by assuming linearity for anthropogenic forcing.
Again: You regressed global surface temperatures against the AMO in order to determine anthropogenic warming. Because the AMO is simply linearly detrended N. Atlantic SST, this procedure would only be correct if AGW is linear. Otherwise you'd be subtracting AGW signal, sweeping some AGW into a box you've labelled "natural" called the AMO.
I already addressed this point: Removing the AMO to determine anthropogenic warming would only be justified if detrending the AMO from 1856-2011 actually removed the trend due to anthropogenic warming.
Predictors are compromised to the extent that warming the globe also changes those predictors. Not all such compromises are created equal.
These barely qualify as compromises. Global warming doesn't force humans to burn fossil fuels. Also, there's no published mechanism (that I know of) linking global warming to volcanic activity.
This is more of a compromise, as I noted: "Even though global warming might indirectly affect ENSO, it's important to note that it hasn't yet: the ENSO index doesn't have a significant 50-year trend. This means it can be subtracted without ignoring AGW."
Because ENSO doesn't have a significant multidecadal trend, this ENSO compromise can't (and doesn't) ignore AGW over multidecadal (i.e. climate) timescales.
I agree: it's better to use an index that isn't temperature.
It wouldn't matter much even if you forgot to regress against ENSO altogether, because ENSO doesn't have a significant multidecadal trend. Regressing against ENSO primarily reduces the uncertainties on the recent multidecadal trend; it doesn't significantly change that trend.
The AMO index is a seriously compromised predictor because warming the globe also warms the N. Atlantic, and anthropogenic forcing is faster after 1950. I've obviously failed to communicate this point, which is why I asked you two questions:
Question 1
Would regressing global surface temperatures against N. Atlantic SST without detrending the SST remove some anthropogenic warming from global surface temperatures?
Yes or no?
Question 2
Now suppose we regress global surface temperatures against N. Atlantic SST after linearly detrending the SST. In other words, we regress against the standard AMO index as Tung and Zhou 2013 did.
Just imagine that anthropogenic forcings increased faster after 1950. In that case, would regressing global surface temperatures against the AMO remove some anthropogenic warming from global surface temperatures after 1950?
Yes or no?
I'll start: my answers are yes and yes. In fact, I think answering yes to question 1 also implies a yes to question 2, but I'm willing to be educated.
Since you never answered these questions, I have to guess at your answers:
Linearly detrended, which means that nonlinear anthropogenic forcing can force a recent upward trend in the AMO. Regardless, your certainty seems to imply that you'd answer "yes" to my question 1. That's fortunate, given that N. Atlantic SST are highly correlated with global surface temperatures:
You've repeatedly pointed out that you used a nonlinear anthropogenic index, and that the result is "very close" to the result using a linear index. Perhaps that's why you think that it's possible to answer yes to question 1 but no to question 2?
If so, I disagree. Because N. Atlantic SST and global surface temperatures are so highly correlated, I think bouke was right to point out that any other predictor will just be a distractor. I suspect that's why you get answers that are "very close" regardless of the assumed anthropogenic index. Unfortunately, I haven't found your code online, and don't have the time to independently reproduce your methodology.
I also respect Isaac Held, which is why I linked that post as well as this one:
"... While the specifics of the calculations of heat uptake over the past half century continue to be refined, the sign of the heat uptake, averaged over this period, seems secure - I am not aware of any published estimates that show the oceanic heat content decreasing, on average, over these 50 years. Accepting that the the sign of the heat uptake is positive, one could eliminate the possibility of [the fraction of the temperature change that is forced] < ~3/4 ..." [Isaac Held]
Note that Isaac Held's analysis is based on thermodynamics, not curve-fitting the AMO. As such, when he claims that the fraction of the temperature change over the last 50 years due to internal variability is less than ~25%, he's summing over all modes of internal variability, not just the AMO. As I've discussed, this is essentially the same conclusion reached by Huber and Knutti 2012.
As KR noted, Anderson et al. 2012 says that less than 10% of the warming over the last 50 years could be due to internal variability.
Your claim of ~40% is inconsistent with studies that base their claims on thermodynamics rather than curve-fitting.
I'm aware that there hasn't been a statistically significant change in the surface warming rate.
In reply to post 75 by Bob Loblaw: I think I have answered your questions in part 2 of my post, in the last section.
In reply to post 77 by MA Roger: My typo. Not 17 years. Some said the hiatus is since 1998, but I don't want to count that because 1997/8 was a warm El Nino. I personally would say the broad leveling off of warming is since 2004/5. You cannot see the leveling off in Figure 9.5, which is up to 2004. The figure up to 2011 using HadCRUT4 is in our paper. 2012 is now available, and it is even lower.
Dr. Tung @80:
Your last section says "It is in the same spirit that the AMO index, which is a mean of the detrended North Atlantic temperature, is used to predict the global temperature change." [Emphasis added]
As Dumb Scientists has given a far more detailed discussion you may wish to respond to, I will temporarily step back again by saying that "in the same spirit" is not particularly convincing. You may have good intentions, and you may have some insight as to why you think that the AMO is good enough, but you haven't conveyed it here and it is a hugely important assumption.
On the other hand, Dumb Scientist is providing a much more convincing argument as to why your methodology causes problems.
Prof. Tung There is no statistically significant evidence for a change in the underlying rate of warming since 1998, so I think it is not scientifically correct to claim there has been a hiatus in global mean surface temperatures since then. The statistical power of the appropriate hypothesis test would be even lower for a trend starting in 2004. As OHC has continued to rise, it seems clear that the apparent hiatus is likely to be due to transport of heat between surface and deep oceans, and so it would be unwise to assume that the apparent hiatus means anything with regard to the forced response. However I think it would be better to discuss this sub-topic on the other thread that Dumb Scientist mentioned so as not to dilute the discussion of the paper.
In short, in order to claim there has been an actual hiatus in warming, rather than merely an artefact of the noise, that hypothesis should be subjected to a formal statistical hypothesis test. The eye is only too prone to seeing patterns in noise that don't actually exist, which is why as scientists we use statistics.
[Dikran Marsupial] link added to make the more appropriate thread for this topic easier to locate.
Dr. Tung - "...I think I have answered your questions in part 2 of my post, in the last section"
I would strongly disagree; Bob Loblaws' points about the circularity in definition of temperature from temperature (or rather, the difficulty of distinguishing between components of the same measure) are unaddressed - forcings have not followed a linear trajectory over this century, hence a linear detrending of the AMO is guaranteed to leave external forcing in that definition. (Aerosol uncertainties, I will point out, do not linearize total forcings.)
Enfield and Cid-Serrano 2010, who you refer to as support for your methods (as I noted before), consider Trenberth and Shea 2006 correct about the failings of a linear detrending, and they instead use a quadratic detrending - a much closer fit to the upwards acceleration in total forcings over the last century. Ting et al 2009 using EOF analysis find that linear detrending is inappropriate for an AMO definition, and they "...argue that the globally averaged surface temperature appears to be a good proxy for the temporal march of externally forced variability and that most of the latter is globally synchronous, albeit nonuniform spatially".
I therefore cannot consider a linearly detrended AMO appropriate in a global warming attribution study - that is contradicted by a significant part of recent literature, as aliasing significant portions of the forced signal.
As a separate piece of evidence, the thermodynamic considerations pointed to by Anderson et al 2012 and by Issac Held (thank you for that interesting reference, Bob) argue that the 40% contribution to warming found with a linearly detrended AMO is inconsistent with observed ocean heat content by a factor of 2-4x. OHC is a constraint upon internal variability, and a 40% internal variability fails that constraint. I'm disappointed that you have not responded to that issue in any fashion.
---
It would be quite interesting to evaluate and compare the attribution percentages under other definitions of the AMO (detrended with global MST or a quadratic, for example) - and whether such estimates are consistent with external constraints such as OHC. But I believe there are significant issues with the attributions you have derived in the current work, issues coming from the AMO definition used - issues which require consideration.
KK Tung @80.
I would suggest that the tiny up-tick at the end of the black trace (which is evidently HadCRUT3 annual data) makes this HadCRUT3 to at least 2005, not 2004.
[JH] Mispelling of Dr Tung's name has been corrected.
Prof. Tung wrote "The CMIP3 models, which do not need internal variability to explain the accelerated warming since 1980, have projections that overshoot the observation in the recent decades, beyond the 95% range."
Please could you provide some supporting evidence for this statement, as far as I am aware, the observations currently lie well within the 95% range of the CMIP3 models (click on the image to access the source).
Last year I downloaded the model runs and was able to reproduce this figure with acceptable accuracy, so I am confident that it is correct (except for the last year of the observations).
In reply to post 78 by Dumb Scientist: You have so many questions in one comment and I have to wait until I have a block of time to answer them. Often one question is convoluted with another and my answers may run the danger of further confusing the readers. You also prefer black and white, yes or no answers. In climate sciences, much is unclear. Let me try the best I could to convey to you my thinking. Your questions involve two groups. One group concerns the linearity of net anthropogenic forcing, and the other group concerns the AMO index.
In part 1 of my post, I attempted to address the claim you raised in your original post that our use of linear regressor (as a placeholder only in the intermediate step) in our multiple linear regression to arrive at an anthropogenic response that is almost linear is circular. This was a technical question and the way I rebutted that claim was to show that our methodology does not depend on what we used for the anthropogenic regressor. We showed this by using a regressor that is not linear. In fact we showed a few such examples. We showed that our procedure is not sensitive to using linear or nonlinear regressors for anthropogenic forcing as long as we add back the residual to the regressed signal. If the true anthropogenic response is linear, but we used a nonlinear regressor that increases faster after 1950, then the residual will show a negative trend after 1950 when it is only supposed to contain noise. When the trend from the residual is added back the combined trend becomes linear. Of course we do not know that the true anthropogenic response is linear, but this example is used here just to illustrate the procedure. This is intended as a technical rebuttal to your claim that our result follows from our assumption of a linear regressor for anthropogenic forcing. This technical rebuttal does not really address what the real anthropogenic forcing is and did not address the choice of the AMO index, the latter does affect the regressed anthropogenic response, as you correctly pointed out. The AMO part was discussed in part 2 of my post.
So what is the shape in time of the net anthropogenic forcing? We know the radiative forcing from the greenhouse gases well (your blue line), but the net forcing has other components that subtract from the greenhouse gas part. They include tropospheric sulfate aerosols, which are highly uncertain. In order for our result of a steady anthropogenic warming to be self consistent with our choice of the AMO index, the net anthropogenic forcing needs to be approximately linear without the ups and down in your red-dashed curve. We claimed that that is not unreasonable given the uncertainty in the aerosol component. This is not an assumption but a proposal. No one knows what the net anthropogenic forcing is with certainty. Therefore there is no inconsistency at our current stage of understanding.
On the AMO index and answering your two questions: Of course anthropogenic forcing can affect the North Atlantic temperature and hence the AMO index, no matter how you define it. It can affect both the secular trend of the N. Atlantic mean temperature and the multidecadal oscillation on top of the secular trend. We are more certain that anthropogenic warming affects the secular trend, but much less certain that it affects the oscillatory part. We know the former because the N. Atlantic temperature trend is less than the global mean trend, and that can be explained by the AMOC (Atlantic Meridional Overturning Circulation) slowing down secularly by the basin-wide warming, with the warm and less saline water sinks less at the Atlantic Arctic. So the Atlantic secular trend has a part that is a direct basin-wide warming by anthropogenic heating and a part that is a result of a change in the AMOC brought about by the warming. The two oppose each other.
At this point one can construct two competing theories. One involves anthropogenic forcing being responsible for both the secular part and the oscillatory part of the N. Atlantic mean temperature. Since the greenhouse gas forcing increase is secular, it cannot be responsible for the oscillatory part of the Atlantic temperature variability. So it falls upon the uncertain tropospheric aerosol to do the job. One needs to come up with an argument on why the aerosol forcing should have such an oscillatory behavior, and builds a model to demonstrate that such variations are sufficient for producing the observed oscillatory response. This job was not attempted by CMIP3 models, but Booth et al (2012) has put forth their HadGEM-ES2 model that produces an oscillatory multidecadal variability. Although the model response in other ocean basins and in subsurface Atlantic are not too consistent with the available observation, I would not rule out this theory, a theory for a forced AMO-like behavior in observation.
The other competing theory is to attribute the oscillatory part to the variations of the AMOC. The mechanism involves the Arctic ice melt and SST feedback on the formation of deep water. This theory is self consistent. The model simulations were consistent with observation. It could also be shown wrong given further evidence, but none of your arguments do it.
Again: I've repeatedly pointed out that the form of the anthropogenic regressor or adding the residual back is not the problem that concerns me. Again, you're implying that anthropogenic warming can only appear in your residual or anthropogenic terms, not your AMO term. I think it could go into your AMO term if anthropogenic warming is nonlinear. So do papers like Enfield and Cid-Serrano 2010, etc.
... nothing has to be true. Your result is always consistent with your choice of AMO index because that choice made your result inevitable. Regressing against the linearly-detrended AMO, which is highly correlated with global surface temperatures, causes any non-linearity to be absorbed by the AMO(t) function. The fact that you get answers which are "very close" regardless of using linear or nonlinear anthropogenic indices to suggest that the regression is more sensitive to the highly correlated AMO(t) function.
But please continue.
You've previously claimed that aerosol time evolution is so uncertain that a linear total anthropogenic forcing lies within its error bars. MA Rodger already asked where that uncertainty bound can be found, and I second his request.
... the fact that the N. Atlantic is filled with water, which has a higher specific heat than the rock making up some of the globe and the fact that oceans can evaporate without limit to shed heat. The land making up some of the globe can (and is) doing that, but those pesky severe droughts limit evaporative cooling on land.
Your mechanism probably plays a role too, especially if the N. Atlantic is compared to other oceans.
I'm not disputing that the AMO exists, and AMOC variations seem like a plausible mechanism. I'm just disputing your curve-fitting claim that ~40% of the warming over the last 50 years can be attributed to a single mode of internal variability, when Isaac Held and Huber and Knutti 2012 used thermodynamics to conclude that all modes of internal variability couldn't be responsible for more than about 25% of the warming. Even if the 10% limit from Anderson et al. 2012 is somehow wrong... didn't you say Isaac Held is one of the most respected climate scientists? I agree.
In reply to post 85 by Dikran: You asked for a figure. I hope my attempt at inserting a figure to a post here works this time: The first figure is from AR4, and the projection was made in 2000. The projection has gone out of the model 95% range of the scenarios shown. The grey band is supposed to be observational uncertainty. The second figure is from CMIP5 by Ed Hawkins. The projection was made in 2005. The more recent projection is almost getting out of the 90% range.
[RH] Whoops. Sorry. The image actually has to be hosted somewhere.
Post 88: My figure insertion did not work. I will try later. Any advice on how to do it?
Also the statement was a little confusing. In the AR4 projection comparing with the observed temperature, the latter has gone out of the model 95% range of all the scenarios shown. In Ed Hawkins' figure showing CMIP5 model projections since 2005, the observation has gone out of 90% of the model range.
[RH] You need to have the image hosted somewhere and then use the image insertion tool (the little tree).
Dr Tung... You first hit the "insert" tab above the comment text box. That where you find the little tree image for image insertions.
Here is the Ed Hawkins graphic as sourced by the Daily Rail's David Rose (who is not the sort of person any self-respecting climatologists should associate with).
The AR4 projections are presented in fig 10.26 but also in fig SPM5 shown here. The shaded areas are 1sd. If you zoom really close in with your rulers (as I did), you will find the 2000 temperature sits at 0.241ºC with the 2012 central projection at 0.457ºC (1 sd +/- 0.18ºC) This would thus require a temperature drop (of 0.08ºC) below the 2000 level for the 2012 observed temperature to be below the AR4 model projection 95% range.
[image deleted]
[Dikran Marsupial] I'm sorry Prof. Tung, SkS doesn't support uploading images to the site, only linking to images that are already hosted on other sites already. Perhaps the easiest approach would be to place them on your own webserver and then link to them here, or possibly use one of the photo sharing services, such as flikr (which is what I have to do for another blog to which I occasionally contribute). Specifically, the data for the image cannot be part of the URL.
I am still having problem inserting figures. I was able to insert a pdf but not a powerpoint figure previously on this site, but no more. I also don't have a server where I can host. SkS need to fix this problem.
I managed to find one figure, the one by Ed Hawkins, on his own twitter site. MA Roger's comment on the person who sourced Hawkins' figure is irrelevant. I thought it better to use a direct source and bypass the second quesssing of the motives of the person who sourced it.
[Dikran Marsupial] I have sent an email suggesting an interim solution. I will raise this issue with the other SkS moderators. I don't think powperpoint images are directly supported by browsers, so perhaps converting it to png, jpg gif etc may resolve the problem.
Still can't insert. But the figure can be found here.
https://twitter.com/ed_hawkins/status/299161479268139009
[Dikran Marsupial] Image added, on my browser (Firefox) clicking over the image on the Twitter brings up a menu with an option to "view image", which loads the image in a new tab on the browser, which then gives a URL that you can use with the SkS image widget. I suspect other browsers have similar functionality but I only use Firefox myself. HTH
Prof. Tung I do not understand the point you are trying to make with this image.
Nobody should expect the observations to lie any closer to the ensemble mean than is indicated by the spread of the model runs (as I have stated before). Note that in 1998 the observations were closer to the (upper) boundary of the 95% than current observations are to the lower boundary. However the 1998 event was not evidence that the ensemble mean was not a good approximation of the forced response, so I see no reason to think that the current observation-ensemble mean difference is indication of a systematic issue, but is probably just internal variability. Of course we are also interested in the physics of internal variability.
The diagram I gave uses the model projections actually used in AR4 and uses the same baseline period that is used in making the projection. Do you agree that it shows that the observations are consistent with the model projection, yes or no? If "no" please explain what is defficient in the figure I presented here.
Note that the choice of baseline has a large effect on the apparent uncertainty of the observations and the models at the boundaries of the baseline period. I suspect this is the issue that James Annan mentions on the twitter thread. Compare the width of the model spread using the two different baseline periods
Note the observations are less close to the edge of the model spread if the longer baseline period is used, as the baselineing procedure minimises the differences between models in the baseline period. The longer the baseline period, the less this can over-fit the variability within the baseline period, so less of the model uncertainty is attenuated.
Dikran Marsupial has performed an analysis which is relevant to this conversation.
Dr. Tung, if you'd like to comment on Dikran's method, we'd all appreciate your insight. Thanks.
In reply post 95 by Dikran and post 96 by Dumb Scientist: I like the tone of our exchanges now. To understand the point I was trying to make, please first do not view my comments as saying there is anything wrong with the IPCC models. My comments concern the forced response vs internal variability. Since I do not know what the forced response is in the observation, I was using the model ensemble mean as a proxy for that. In fact this is an assumption that the model is perfect. Now we cannot do ensemble mean of the observation, because our climate is just one realization and we do not have the other ensemble members. So we cannot compare observation's forced response with the model's forced response. My statements were never intended to be a comparison of the two and see if the models are correctly simulating the real forced response. Subject to the caveat of my assumption of perfect models, my statement concerns the presence of internal variability. When the observation is below the model ensemble mean, I tentatively suggest that the explanation could be that there is an internal variability that is in a cool phase in the observation but is not (and should not be) in the model ensemble mean. The point I made previously was why we need it now during the hiatus period and not during the period of accelerated warming.
In reply to post 95 by Dikran: I liked your work investigating the effect of the change in baseline offsetting on the apparent model uncertainty.
Just to be clear, my comment #96 didn't refer to Dikran's comment #95 above. I linked to Dikran's comment on another page which is much more interesting.