Can we trust climate models?
Posted on 24 May 2011 by Verity
This is the first in a series of profiles looking at issues within climate science, also posted at the Carbon Brief.
Computer models are widely used within climate science. Models allow scientists to simulate experiments that it would be impossible to run in reality - particularly projecting future climate change under different emissions scenarios. These projections have demonstrated the importance of the actions taken today on our future climate, with implications for the decisions that society takes now about climate policy.
Many climate sceptics have however criticised computer models, arguing that they are unreliable or that they have been pre-programmed to come up specific results. Physicist Freeman Dyson recently argued in the Independent that:
“…Computer models are very good at solving the equations of fluid dynamics but very bad at describing the real world. The real world is full of things like clouds and vegetation and soil and dust which the models describe very poorly.”
So what are climate models? And just how trustworthy are they?
What are climate models?
Climate models are numerical representations of the Earth’s climate system. The numbers are generated using equations which represent fundamental physical laws. These physical laws (described in this paper) are well established, and are replicated effectively by climate models.
Major components of the atmosphere system such as the oceans, land surface (including soil and vegetation) and ice/snow cover, are represented by the current crop of models. The various interactions and feedbacks between these components have also been added, by using equations to represent physical, biological and chemical processes known to occur within the system. This has enabled the models to become more realistic representations of the climate system. The figure below (taken from the IPCC AR4 report, 2007) shows the evolution of these models over the last 40 years.
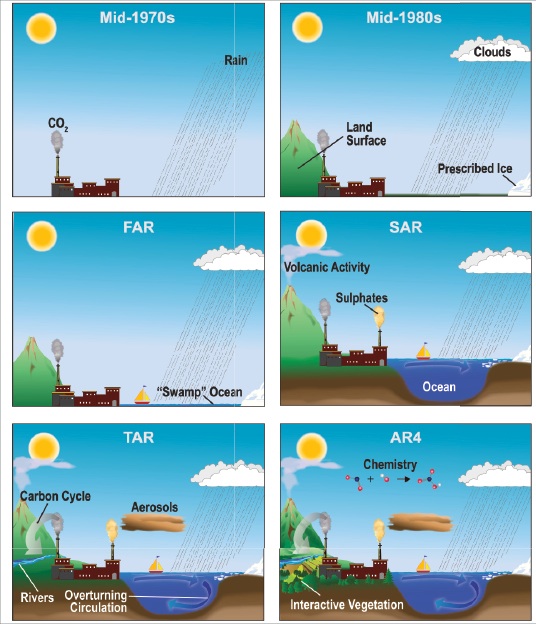
Models range from the very simple to the hugely complex. For example, ‘earth system models of intermediate complexity’ (EMICs) are models consisting of relatively few components, which can be used to focus on specific features of the climate. The most complex climate models are known as ‘atmospheric-oceanic general circulation models’ (A-OGCMs) and were developed from early weather prediction models.
A-OGCMs treat the earth as a 3D grid system, made up of horizontal and vertical boxes. External influences, such as incoming solar radiation and greenhouse gas levels, are specified, and the model solves numerous equations to generate features of the climate such as temperature, rainfall and clouds. The models are run over a specified series of time-steps, and for a specified period of time.
As the processing power of computers has increased, model resolution has hugely improved, allowing grids of many million boxes, and using very small time-steps. However, A-OGCMs still have considerably more skill for projecting large-scale rather than small-scale phenomena.
IPCC model projections
As we have outlined in a previous blog, the Intergovernmental Panel for Climate Change (IPCC) developed different potential ‘emissions scenarios’ for greenhouse gases. These emissions scenarios were then input to the A-OGCM models. Combining the outputs of many different models allows the reliability of the models to be assessed. The IPCC used outputs from 23 different A-OGCMs, from 16 research groups to come to their conclusions.
Can we trust climate models?
'All models are wrong, but some are useful' George E Box
There are sources of uncertainty in climate models. Some processes in the climate system occur on such a small scale or are so complex that they simply cannot be reproduced in the models. In these instances modellers use a simplified version of the process or estimate the overall impact of the process on the system, a procedure called ‘parameterisation’. When parameters cannot be measured, they are calibrated or ‘tuned’, which means that the parameters are optimised to produce the best simulation of real data.
These processes inevitably introduce a degree of error - this can be assessed by sensitivity studies (i.e. systematically changing the model parameters to determine the effect of a specific parameter on model output).
Other sources of potential error are less predictable or quantifiable, for example simply not knowing what the next scientific breakthrough will be, and how this will affect current models.
The IPCC AR4 report evaluated the climate models used for their projections, taking into account the limitations, errors and assumptions associated with the models, and found that:
“There is considerable confidence that AOGCMs provide credible quantitative estimates of future climate change, particularly at continental and larger scales.”
This confidence comes from the fact that the physical laws and observations that form the basis of climate models are well established, and have not been disproven, so we can be confident in the underlying science of climate models.
Additionally, the models developed and run by different research groups show essentially similar behaviour. Model inter-comparison allows robust features of the models to be identified and errors to be determined.
Models can successfully reproduce important, large-scale features of the present and recent climate, including temperature and rainfall patterns. However, it must be noted that parameter ‘tuning’ accounts for some of the skill of models in reproducing the current climate. Furthermore, models can reproduce the past climate. For example simulations of broad regional climate features of the Last Glacial Maximum (around 20,000 years ago) agree well with the data from palaeoclimate records.
Climate models have successfully forecast key climate features. For example, model projections of sea level rise and temperature produced in the IPCC Third Assessment Report (TAR - 2001) for 1990 – 2006 show good agreement with subsequent observations over that period.
So it is a question of whether the understanding of the uncertainties by the climate science community are sufficient to justify confidence in model projections, and for us to base policy on model projections. Whether we chose to accept or ignore model projections is a risk. As Professor Peter Muller (University of Hawaii) put it in an email to the Carbon Brief:
“Not doing anything about the projected climate change runs the risk that we will experience a catastrophic climate change. Spending great efforts in avoiding global warming runs the risk that we will divert precious resources to avoid a climate change that perhaps would have never happened. People differ in their assessment of these risks, depending on their values, stakes, etc. To a large extent the discussion about global warming is about these different risk assessments rather than about the fairly broad consensus of the scientific community.”
It should be noted that limits, assumptions and errors are associated with any model, for example those routinely used in aircraft or building design, and we are happy to accept the risk that those models are wrong.
For more information about climate models:
- Climate Models: An Assessment of Strengths and Limitations. A Report by the U.S. Climate Change Science Program.
- Climate scientists answer climate model FAQs at Real Climate: Part 1 and Part 2.
- An in-depth review of climate model history can be found here.
- “Constructing climate knowledge with computer models”, Professor Peter Müller (University of Hawai’i at Manoa) – Paper discussing all aspects of climate model uncertainty (behind paywall).
- Informative Google Tech talk given by Professor Inez Fung (Berkeley Institute of the Environment)































 Arguments
Arguments






























[DB] Apologies, as you must have spent substantial time and effort developing and posting your comment, but the snipped majority falls outside the scope of this thread.
As dana1981 points out, you are welcome to break up your longer comment into components and post those on more appropriate threads for others to read & discuss if you wish (the Search function will find ample threads; select the most appropriate for the comments).
Alternatively, you could post the entire comment as a blog post on your own blog and then provide a link here for interested parties to follow.