Radiative Balance, Feedback, and Runaway Warming
Posted on 26 February 2012 by Chris Colose
Skeptical Science has previously discussed the topic of feedbacks and why the existence of positive feedbacks (i.e., those feedbacks that amplify a forcing) do not necessarily lead to runaway warming, or even to an inherently "unstable" climate system. I also wrote on it at RealClimate (and Pt. 2). This was brought up again in Lord Christopher Monckton's response to SkepticalScience, where he asserted:
"First, precisely because the climate has proven temperature-stable, we may legitimately infer that major amplifications or attenuations caused by feedbacks have simply not been occurring...A climate subject to the very strongly net-positive feedbacks imagined by the IPCC simply would not have remained as stable as it has."
I wanted to revisit the subject in order to take a different approach on the subject of positive feedbacks. This involves the relationship between Earth's surface temperature and outgoing infrared radiation (the energy Earth emits to space). Determining how the outgoing longwave radiation (OLR) depends on surface temperature and greenhouse content is a fundamental determinant to any planetary climate.
I'll begin with very trivial, ideal cases, and then slightly build up in complexity in order to relate the problem to climate sensitivity. By the end, it should be clear why positive feedbacks can exist that inflate climate sensitivity but do not necessarily call for a runaway warming case. We'll also see a scenario, commonly discussed by planetary scientists, in which it does lead to a runaway.
First, we begin with the simplest case in which the Earth has no atmosphere and essentially acts as a perfect radiator. In this case, the outgoing radiation is given by the Stefan-Boltzmann equation OLR=σT4. T is temperature. σ is a constant, so the equation means that the outgoing radiation grows rapidly with temperature, (to the power of four) as shown below.
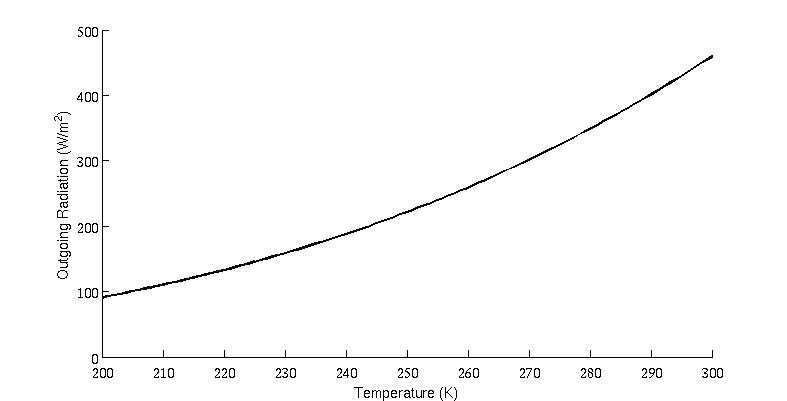
Figure 1: Plot of OLR vs. Surface temperature for a perfect blackbody
In the next case, suppose that we add some CO2 to the atmosphere (400 ppm). The atmosphere here is completely dry (and therefore no water vapor feedback). In this example, the addition of CO2 will reduce the OLR for any given temperature, since the atmosphere absorbs some of the exiting energy. This is displayed with the red curve in Figure 2 (the black curve is from above for reference).
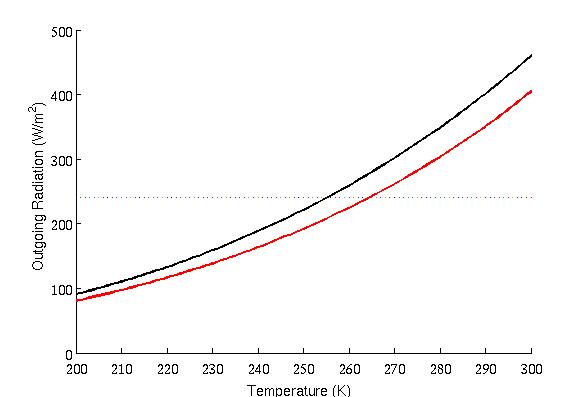
Figure 2: Relationship between OLR and surface temperature for a blackbody (black curve) and with 400 ppm CO2 (red curve). The horizontal line is the absorbed solar radiation.
Also plotted in Figure 2 is a horizontal line at 240 W/m2, which corresponds to the amount of solar energy that Earth absorbs. In equilibrium, the Earth receives as much solar energy as it does emit infrared radiation. Therefore, in the above plot, the points at which the horizontal line intersect the black/red lines will correspond to the equilibrium climates in this model. Note that the red line makes this intersection at a higher surface temperature, which is the greenhouse effect.
Now let's step up the complexity a bit. We'll throw in some water vapor into the model, but not just a fixed amount of water vapor. This time, we'll also let the water vapor concentration increase as temperature increases. Water vapor is a good greenhouse gas, so now the infrared absorption grows with temperature. This is the water vapor feedback. The blue line in the next figure is the OLR for a planet with the same 400 ppm CO2, in addition to this operating feedback.
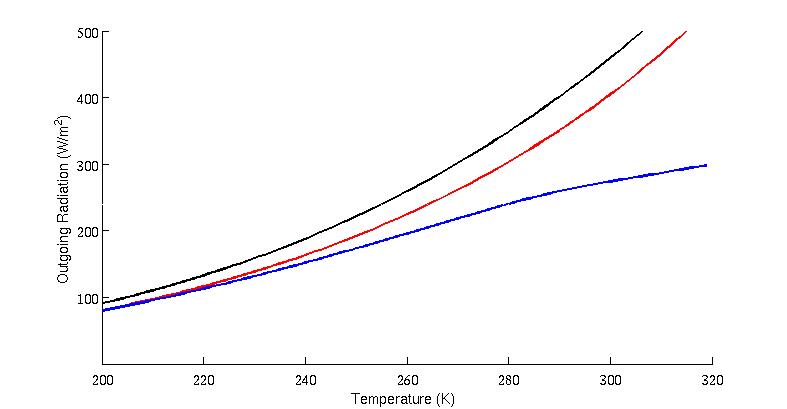
Figure 3: Relationship between OLR and surface temperature, as above, but with a constant relative humidity atmosphere (blue line, implying increasing water vapor with temperature)
In this figure, we see that the OLR does not depend very much on the water vapor at low temperatures. This makes sense, because at temperatures this cold (such as during a snowball Earth), there is so little water vapor in the air. However, at temperatures similar to the modern global mean and warmer, the OLR drops tremendously and the the T4 dependence instead becomes much flatter. We'll get a more clear picture of that means for climate sensitivity in the next diagram.
In the next diagram, I've removed the red curve for convenience. But I've added two horizontal lines this time. You can think of this as two possible values for the incoming solar radiation.
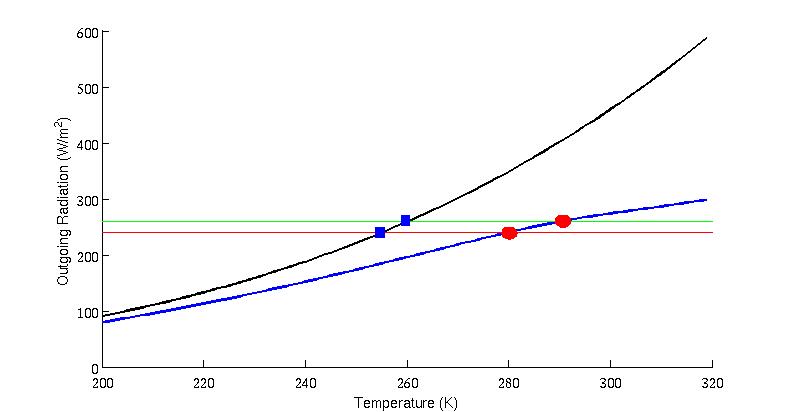
Figure 4: OLR vs. surface temperature for a blackbody (black curve) and an atmosphere with CO2 and a water vapor feedback (blue curve). The horizontal lines give two values for the absorbed incoming solar radiation, and the colored shapes give possible equilibrium points. On the trajectory where water vapor exists, sensitivity is enhanced because the temperature difference between the two red circles (as sunlight goes up) is greater than the difference between the two blue squares.
To interpret Figure 4, suppose that we increase the amount of sunlight that the Earth gets, which means we jump from the red to the green line in the above figure. If the Earth were a blackbody (black curve) then the temperature change that results from this would just be the difference between the values at the two blue squares. However, in a world with a water vapor feedback, the temperature difference is given by the distance between the two red circles. We can infer from this that water vapor has increased climate sensitivity, yet it did not cause a runaway warming effect.
Now let's consider one more case. Notice in the previous diagram that at very high temperatures, the OLR starts to flatten out, and indeed eventually can become almost flat. This is due to the rapid increase in water vapor (and infrared absorption) as temperature goes up. But suppose we pump up the amount of sunlight that the Earth gets to much higher values than in the last figure. This new value is shown by the horizontal green line in the figure below.
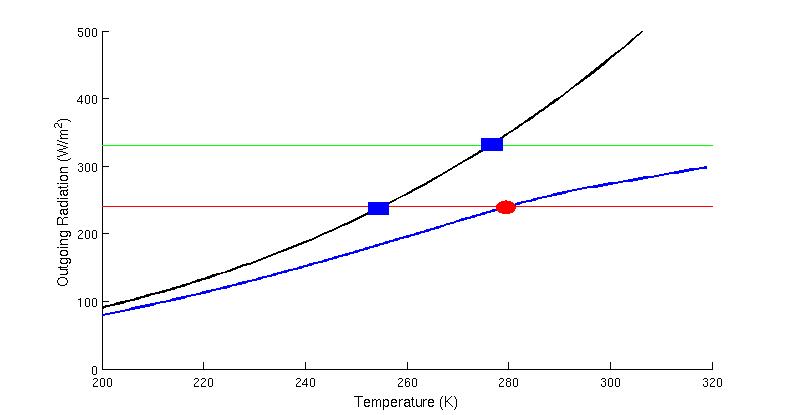
Figure 5: As above, but the green line corresponds to higher incoming solar radiation.
Once again, if we follow the black curve (with no atmosphere), then we get an expected increase in temperature as the amount of sunlight goes up. But if we follow the blue curve (the system with an operating water vapor feedback), then something strange happens.
At some point the OLR becomes so flat, that it can never increase enough to match the incoming sunlight. In this case, it actually becomes impossible to establish a radiative equilibrium scenario, and the result is a runaway greenhouse. This is the same phenomenon planetary scientists talk about in connection with the possible evolution of Venus or exoplanets outside our solar system. The system will only be able to come back to radiative equilibrium once the rapid increase of water vapor mass with temperature ceases, which in extreme cases may not be until the whole ocean is evaporated.
From these figures, we can readily see the fallacy in "positive feedbacks imply instability" type arguments. There is in fact a negative feedback that always tends to win out in the modern climate. This is the increase in planetary radiation emitted to space as temperature goes up. Positive longwave radiation feedbacks only weaken the efficiency at which that restoring effect operates. Instead of the OLR depending on T4, it might depend on T3.9, or maybe even T3 at higher temperatures; eventually the OLR becomes independent of the surface temperature altogether. I haven't discussed shortwave feedbacks, such as the decrease in albedo as sea ice retreats. That only raises the position of the horizontal lines slightly, allowing for a warmer equilibrium point, but in no way compromises the argument.
In fact, the same sort of argument can be applied if we let the albedo vary with temperature (and so the absorbed solar radiation is no longer given by a horizontal line). The opposite extreme, a snowball Earth, can then be thought of as a competition between the decreased longwave radiation to space as the planet cools, and the increased reflection as the planet brightens (when the ice line is advancing toward the equator). As with a runaway greenhouse, it's not inevitable that this occurs, as is evident from times in Earth's history when ice advanced but did not reach the equator.
As a final note, it's worth mentioning that it is virtually impossible to trigger a true runaway greenhouse in the modern day by any practical means, at least in the sense that planetary scientists use the word to describe the loss of any liquid water on a planet. The most realistic fate for Earth entering a runaway is to wait a couple billion years for the sun to increase its brightness enough, such that Earth receives more sunlight than the aforementioned outgoing radiation limit that occurs in moist atmospheres. None of this means that climate sensitivity cannot be relatively high however.
Note: Except for the first graph, all computations here were done using the NCAR CCM radiation module embedded within the Python Interface for Ray Pierrehumbert's supplementary online material to the textbook "Principles of Planetary Climate." The lapse rate feedback is included as an adjustment to the moist adiabat. I've assumed near-saturated conditions are maintained (constant 100% relative humidity) with temperature, although the argument is qualitatively similar with lesser RH values.
This post has been adapted into the Advanced rebuttal to "Positive feedback means runaway warming"































 Arguments
Arguments























 0
0  0
0 Here the y-axis is the feedback factor,f, typically associated with the equation 1/1-f. Climate sensitivity is proportional to 1/1-f. More specifically it is *equal to* CS=b/1-f where b is the response you'd get in a system that only had the Stefan-Boltzmann response operating. Thus, in the limit where we have no feedbacks, f=0 and the equation reduces to CS=b. That is, you'd get the response from just the Stefan-Boltzmann response.
In the above graph, the "all" feedback factor is positive, f=0.6 or so. This means that CS = b/0.4 = 2.5b (i.e., climate sensitivity is inflated by a factor of 2.5). Note however that the Stefan-Boltzmann response is not included in the graph.
Here the y-axis is the feedback factor,f, typically associated with the equation 1/1-f. Climate sensitivity is proportional to 1/1-f. More specifically it is *equal to* CS=b/1-f where b is the response you'd get in a system that only had the Stefan-Boltzmann response operating. Thus, in the limit where we have no feedbacks, f=0 and the equation reduces to CS=b. That is, you'd get the response from just the Stefan-Boltzmann response.
In the above graph, the "all" feedback factor is positive, f=0.6 or so. This means that CS = b/0.4 = 2.5b (i.e., climate sensitivity is inflated by a factor of 2.5). Note however that the Stefan-Boltzmann response is not included in the graph.







Comments