Climate Science Glossary

Term Lookup

Enter a term in the search box to find its definition.

Settings

Use the controls in the far right panel to increase or decrease the number of terms automatically displayed (or to completely turn that feature off).

Term Lookup

Settings

All IPCC definitions taken from Climate Change 2007: The Physical Science Basis. Working Group I Contribution to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Annex I, Glossary, pp. 941-954. Cambridge University Press.

Home Arguments Software Resources Comments The Consensus Project Translations About Support

Bluesky Facebook LinkedIn Mastodon MeWe

Twitter YouTube RSS Posts RSS Comments Email Subscribe


Climate's changed before
It's the sun
It's not bad
There is no consensus
It's cooling
Models are unreliable
Temp record is unreliable
Animals and plants can adapt
It hasn't warmed since 1998
Antarctica is gaining ice
View All Arguments...



Username
Password
New? Register here
Forgot your password?

Latest Posts

Archives

Greenland ice mass loss after the 2010 summer

Posted on 1 November 2010 by John Cook

The National Oceanic and Atmospheric Administration (NOAA) recently released the Arctic Report Card. The report contains a wealth of information about the state of climate in the Arctic circle (mostly disturbing). Especially noteworthy is the news that in 2010, Greenland temperatures were the hottest on record. It also experienced record setting ice loss by melting. This ice loss is reflected in the latest data from the GRACE satellites which measure the change in gravity around the Greenland ice sheet (H/T to Tenney Naumer from Climate Change: The Next Generation and Dr John Wahr for granting permission to repost the latest data).

 

Figure 1: Greenland ice mass anomaly - deviation from the average ice mass over the 2002 to 2010 period. Note: this doesn't mean the ice sheet was gaining ice before 2006 but that ice mass was above the 2002 to 2010 average.

The ice sheet has been steadily losing ice and the rate of ice loss has doubled over the 8 year period since gravity measurements began. The accelerating ice loss is independently confirmed by GPS measurements of uplifting bedrock. The GRACE data gives us an insight into why Greenland is losing ice mass at such an accelerating rate - ice loss has spread from the south east all the way up the west coast:

 

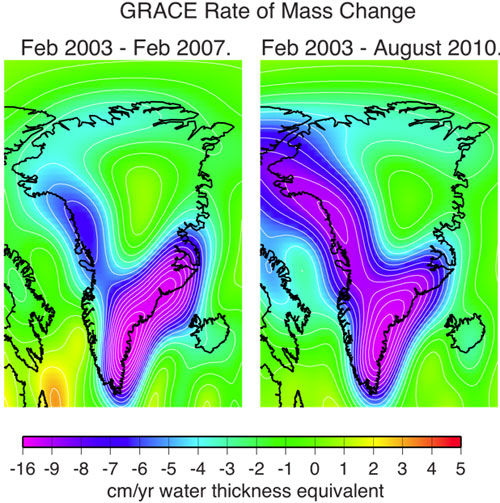
Figure 2: rate of mass change from Greenland over 2003-2007 and 2003-2010 periods. Mass loss rate has spread up the north western ice margin over the last few years. 

0 0

Printable Version  |  Link to this page

Comments

1  2  Next

Comments 1 to 50 out of 53:

  1. That second image is terrifying - like a great purple cloud of doom. We really are up the proverbial creek without, it seems, a paddle.
    0 0
  2. Still, not to worry, CO2 is, after all, a plant food, and I'm sure Greenland (note the name) was ice free in the MWP (now free to blossom after we broke the hockey stick) but whatever, sunspots, volcanoes, it's all perfectly natural, and any link to any kind of human activity of any kind is obviously wrong cause Ayn Rand said so.
    0 0
  3. This puts me in a very difficult position. When looking at purchasing waterfront property, do I buy at the +6m level, or +20m, or what??? More seriously, this is, as David Horton stated, a terrifying image. Whatever we do now, the rollercoaster has tipped over the starting ramp, and we're in for one hell of a ride...
    0 0
  4. The color-coded map is indeed nightmarish, and not just because it's still Halloween (at least here in the US). I wish that when the mass loss graph was drawn it didn't have the zero line/average indicated that way, though. I've had trouble in showing this to people and watching them make the mistake that John warns people about in the caption. I think it might be better to label the Y axis with 0 at the top, and add a blue line at the average, say.
    0 0
    Response: I've had to explain that graph so many times to confused readers, I decided to get proactive and explain it in the caption this time. I don't like using the term 'anomaly' as it's a scientific term that has little meaning to the average person. But when I use change or variation, it seems to create even more confusion so I opted for the technically more precise but more opaque anomaly.
  5. In response to the graph issue - perhaps the clearer option for general consumption would be to graph "Ice mass change since 2002". That way, the zero would be at the top, and it should be clear that the change has been overwhelmingly negative.
    0 0
  6. If the sewage pumps stop +6m isn't enough even today, the backpressure from the ocean waves can reach pretty high. One way to show this kind of data would be to title it:'Greenland mass change 2002-2010', and set the zero at the beginning of the measurement period. It's commonly done thus in faunistics. If the direction of the change is the only thing needed to show there's no need to compute the average, shortly. And I see Bern already said this.
    0 0
  7. Can we quantify what this means for likely sea level rise? My understanding was that any Greenland melt was expected to take several hundred years; how does this rate compare?
    0 0
  8. The scariest feature of the Grace rate plots is that the level of the Baffin, Newfoundland and Greenland seas have been dropping over the past 9 years. However, if we assume that the rate contours are artifically extended into these seas by the contour software and should really be zeroed at the coastline, then it appears that the rate of loss in southeast Greenland has slowed/dropped by at least 3 cm/yr while the rated has increased by about 4cm/yr in the west. Pretty poor/confusing data plot!
    0 0
  9. Seconding Doug H's comment; the canary is dying and we're still digging. Related material: Khan, S. A., J. Wahr, M. Bevis, I. Velicogna, and E. Kendrick (2010), Spread of ice mass loss into northwest Greenland observed by GRACE and GPS, Geophys. Res. Lett., 37, L06501, doi:10.1029/2010GL042460. http://www.agu.org/journals/ABS/2010/2010GL042460.shtml (pay wall) http://www.sciencedaily.com/releases/2010/03/100323161819.htm I know, clunky link usage, but in this case the URL identifies the source and that seems significant to me in this case.
    0 0
  10. I presume the reason for using the average as the base level is that if you just compute change from the starting year it could, and would, be argued, that the first year just happened to be an abnormally high (in this case) year. However given the smooth shape of this anomaly graph it is clear that there was nothing abnormal about 2002, as it turned out, and that therefore you could switch to making it the zero level. Or am I misunderstanding something statistical?
    0 0
  11. On the subject of the anomaly zero point, surely the problem occurs because the average is calculated from such a short period? I'm sure this graph would be less ambiguous - and more compelling - if the average was calculated like all trends, from a 30 year period. Focussing on such a short period seems to compound the problem, and does rather contradict our oft-repeated claim that only trends are valid, not short term data. Still bloody terrifying though. There are not many reasons to be glad I'm nearly 60, but contemplating the outcomes of AGW I'm not going to see (because they will be beyond my personal 'event horizon') is actually one of them!
    0 0
  12. @gpwayne: I don't expect to see all that many outcomes of AGW myself - probably another 60-odd years to go for me, barring any major medical advances (although I have a friend who used said he "fully expects lifespans to be extended into the centuries range soon", and decided to go on a major health & fitness program to make sure he was around to see it!). That aside, though, if things proceed as the best science suggests, then by 2060 we'll be seeing some pretty amazing things happening. What my baby daughter will get to see in her lifetime will, of course, be a different question entirely! Going by the info in this and other posts, Greenland will be melting / shedding ice for a *long* time to come. But with a few more decades of data, it might become *very* difficult to deny it's happening. We might also see some more dramatic happenings in West Antarctica, and who knows what sort of weather we'll have. Interesting times ahead...
    0 0
  13. Where are the heros that will save the world? Who? Us? Ok, tell us what I must do!
    0 0
  14. beam me up scotty. Since Jim Kirk and the Enterprise aren't streaking across the galaxy on a resue mission - and lets face it, there is only so much you can do by reconfiguring the deflector dish AGAIN. So, yep. Its up to us. So: "Ok, tell us what I must do" Convince Others. Of the reality, Severity and above all the Urgency. Individually we can do nothing, only when we all act together. If you were discussing what you could do to solve World Poverty the answer is that you individually could. For one person. You could lift another person out of poverty. Just not everyone. But your individual actions alone could solve the problem for another person. With AGW, you can't solve the problem for one person. Either it is solved for everyone, or it is not solved. So individual action counts for little when it is only a few individuals. So the most useful thing anyone can do is be part of arguing the case. The case for the mobilisation of Humanity against the greatest crisi in Human History. This may truely be a situation where the Pen IS mightier than the Sword. Or the Dollar, Or the Solar Panel on your roof. This is about mobilising Humanity. Everything else is a well intentioned sideshow.
    0 0
  15. Climate Sanity has a post that should help visualise what it probably all means in terms of volume and sea levels. Conversion factors for ice and water mass and volume
    0 0
  16. Wasn't there a problem with GRACE and rebound giving inaccurate readings? Has this been sorted and accounted for in this Report card?
    0 0
  17. gpwayne: "I'm sure this graph would be less ambiguous - and more compelling - if the average was calculated like all trends, from a 30 year period." Isn't that a bit tricky if you only have 8 years of data? http://en.wikipedia.org/wiki/Gravity_Recovery_and_Climate_Experiment Launch date: March 17, 2002 To me what's compelling about this graph is how clean the data is: how well it follows the quadratic fit with the annual variation. The red line is a quadratic fit, isn't it? What period was it fitted over?
    0 0
  18. gpwayne #11: "Focussing on such a short period seems to compound the problem, and does rather contradict our oft-repeated claim that only trends are valid, not short term data." The length of time needed to determine a valid trend increases as the amount of 'noise' in the data does. If you look at the Mauna Loa CO2 data you've got a small annual cycle and a very smooth upward trend which can be clearly seen from just a few years' data (though we happen to have decades of confirmation). Temperature records on the other hand bounce all over the place and thus require much longer periods to determine a trend. The Greenland mass loss data seems to be somewhere in the middle... there is some noise, but note that every annual peak and every annual low is lower than the previous year. The 'noise' isn't great enough to ever 'break' the downward trend... just providing fluctuations around it. That is, if anything, a much clearer picture than we get from the noisier data sets... even when we have more data for them.
    0 0
  19. Lazarus @ 16 - Wu 2010 employ a novel technique, using (sparse) GPS data to calculate for glacio-isostatic uplift. No doubt it will take time for the scientific community to ascertain it's value/accuracy, but it is at odds with estimates using other methods. Going out on a limb here, Wahr and Velicogna, were authors of earlier GRACE studies using the GIA model estimates, so I doubt they've employed WU's methods. There is an upcoming post on the topic.
    0 0
  20. 16.Lazarus I think you're referring to the 2010 paper by Wu et al in Nature Geoscience. Simultaneous estimation of global present-day water transport and glacial isostatic adjustment 15 AUGUST 2010 | DOI: 10.1038/NGEO938 It's not referred to in the Arctic Report Card. Neither is Murray et al 2010 Ocean regulation hypothesis for glacier dynamics in southeast Greenland and implications for ice sheet mass changes JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 115, F03026, doi:10.1029/2009JF001522, which suggest alternative explanations for de-glaciation in SE Greenland. John is it possible that the information is "mostly disturbing" and David Horton finds things terrifying because this report card is biassed in presenting such data? The attempted link between AGW and the severe winter in Europe and the US last year seems particularly shameful.
    0 0
  21. Murray et al 2010 I've only access to the abstract, but it suggests icesheet-ocean interactions are the primary control on the rate of ice discharge in SE Greenland glaciers. Hardly a startling revelation.
    0 0
  22. Icesat which is a separate data set is showing a loss of a similar magnitude to the GRACE data set, that is indicating the result is robust. From a submitted paper Sørensen et al (2010) "We find an annual mass loss of the Greenland ice sheet of 210 ± 21 Gt yr−1 in the period from October 2003 to March 2008. This result is in good agreement with other studies of the Greenland ice sheet mass balance, based on different remote sensing techniques". This year for northwestern Greenland the snowline's were quite high from early in the melt season. This is one of the factors that raised the vulnerability of the Petermann Glacier. Going forward it will raise the vulnerability of Ryder Glacier and others.
    0 0
  23. HR #20: "The attempted link between AGW and the severe winter in Europe and the US last year seems particularly shameful." Ummm... the 'severe' winter in Europe and the US last year was unquestionably due to cold winds out of the Arctic. Arctic winds do not normally reach that far South. Ergo, the cold winter was either just a random event with no particular long term significance OR evidence of a change in Arctic wind patterns. Guess what has been predicted to change Arctic wind patterns? If you said 'global warming' you might just understand why '2 + 2 may equal 4' is not a "particularly shameful" link.
    0 0
  24. #23: "you might just understand why '2 + 2 may equal 4' is not a "particularly shameful" link." Reminds me of an old oil field joke, which answers the question 'how much is 2+2?' with 'what would you like it to be?' Here's some perspective on winter 2010: The winter of 2009/2010 was characterized by record persistence of the negative phase of the North-Atlantic Oscillation (NAO) which caused several severe cold spells over Northern and Western Europe. This somehow unusual winter with respect to the most recent ones arose concurrently with public debate on climate change ... We show however that the cold European temperature anomaly of winter 2010 was (i) not extreme relative to winters of the past six decades ... The winter 2010 thus provides a consistent picture of a regional cold event mitigated by long-term climate warming. Isn't it shameful how some people have their own mathiness?
    0 0
  25. I don't think it's shameful to suggest AGW played a role in last winter. However, you can see how the effect of AGW on climate can be confusing to the lay person. Loss of sea-ice = equals changing wind patterns = cold winter in Europe BUT not so cold as similar conditions (extreme negative NAO) would have produced in past because AGW has shifted the baseline. Doesn't exactly trip off the tongue. Then there is the issue of what a bad winter is, and that definitition changed depending on where you were. It was colder than usual in the SE US last year, but not here in the NE US. Still it was considered a "bad" winter because of the amount of snow we had up here. That was a consequence of the extreme negative NAO combined with an ongoing El Nino that feeds moisture into the SE US. AGW could have affected the extent of the AO/NAO (through Arctic Sea ice) and the water vapor available for precip. Back to Greenland. Are those focal areas of ice loss related to particular sealevel exit points for the inland icesheet?
    0 0
  26. Another study from September showed that the isostatic adjustment from the last glacial period is causing the ice loss to be overstated by about double. The recent article gives estimates of 104 +/- 23 Gt/yr for Greenland and in West Antarctica the loss is 62+/- 32 Gt/yr. So which is correct? The studies that give the higher results don't take the adjustment into account. Stating that the loss is 200+ Gt/yr as fact when there are “published” articles that give results that are half as much is a bit disingenuous. When taken into account with the other recent article that indicates that the Arctic was ice free during the summer in the early Holocene which would also indicate that the ice loss was even greater during that period than the current period. There is a good reason to be skeptical about the significance of the current behavior. John Kehr The Inconvenient Skeptic
    0 0
  27. TIS... Your second link is broken. The last info I got regarding when the Arctic was last ice free was this video lecture by Professor David Barber where he states that there is currently debate over whether the last time the Arctic was ice free was 1 million years ago or 14 million years ago.
    0 0
  28. TIS... I'd also say that you're jumping the gun a bit to call it "disingenuous." If the data had been available for 5 years and newer data were fully incorporated and the old data were being presented, THAT would be disingenuous. (BTW, this is a technique continually applied to the "hockey stick" issue.) If you look, Wu 2010 states in the abstract that "We conclude that a significant revision of the present estimates of glacial isostatic adjustments and land–ocean water exchange is required." That is from a paper published just 9 weeks ago, about the same time the GRACE data above is published. I'm confident everyone is reviewing Wu's findings. You have to give science just a little bit of time to do it's work. As you very well know, these issues are highly complex and take a lot of time to research in full detail.
    0 0
  29. #26: "So which is correct?" Is that the best question to ask? Here is the key message: “While differences in these studies still exist,” Abdalati concludes, “collectively, they very convincingly paint a picture of the Greenland Ice Sheet as having been close to balance in the 1990s, contributing a small amount to sea level, but becoming significantly out of balance and losing a substantial amount of ice to the sea in the last several years.”
    0 0
  30. John Kehr @26, Can you please refrain from suggesting nefarious goings on concerning these Greenland Ice Sheet (GIS) data? Thanks. It baffles me that we can have these data/events staring us in the face and yet some people choose to think of creative ways of dismissing or questioning these troubling revelations. First, the studies using GRACE (e.g., Velicogna 2009), data do apply isostatic adjustments to the data--"GIA [Glacial Isostatic Adjustment] signal is removed from the GRACE data using independent models as described by Velicogna and Wahr [2006a, 2006b]." Second, as far as I can tell, IF Wu et al's (2010) proposed GIAs are correct (and there are reasons to believe that that they not be appropriate), they affect only the absolute values, not the trend. Regardless, data from multiple, independent groups and measurement platforms do point towards an accelerating rate of ice loss (e.g., Jiang et al. 2010). Third, surely you can do better than arguing the equivalent of "well the climate is always changing so this is nothing unusual". Climate scientists and glaciologists of course know very well that ice sheets are dynamic, complex systems which respond to multiple drivers, and consequently that they have grown and receded in the past. What is happening now with not only the GIS, but WAIS, Arctic sea ice, and other terrestrial glaciers/ice sheets and other metrics concerns people who study the cryosphere for a living, and so it should also concern reasonable and prudent people. Polyak et al. (2010) are concerned and not what is happening now with Arctic sea ice and note that what is happening can not be attributed to natural variability...do you really think that you know better than they do? This is still relatively early days in the AGW story, so do not make the mistake of equating what is happening now to what the situation will be decades or centuries form now-- the GIS (and WAIS) will, in all likelihood, look very much different by then. You can choose to ignore this image, but do so at the peril of future generations: Figure GL3. Difference (days) in summer 2010 melt duration compared to 1979-2007 mean, after Mote (2007). The 2400 m elevation contour is included to illustrate higher elevations of melting over the southern ice sheet. [Along the southwestern ice sheet, the number of melting days in August has increased by 24 days over the past 30 years-- NOAA]
    0 0
  31. Muoncounter @29, Thanks for that link. What is interesting is that they were investigating differences between different methodologies and data sets back in 2007 (the article is dated August 2007). This is exactly how science works. I also found this statement concerning: "Abdalati says he is convinced that the Greenland Ice Sheet will continue to shrink at a significant and, perhaps, accelerating rate. Already he and his colleagues have new studies underway in which they are investigating the sensitivity of the ice sheet to rising temperatures and the specific mechanisms by which the ice sheet responds to increased warmth." [August 2007]. Well look what has happened just three years after he said that.... Do I want to read what Abdalati said above? No, of course not, but I'm not going to waste yet more time by going into denial as some in this thread are doing? Again, No.
    0 0
  32. #31: "look what has happened just three years after he said that...." Yep: even in climate science, despite 'all the uncertainty' some predictions turn out right. Makes you wonder if all those separate lines of evidence mean something ...
    0 0
  33. Rob Painting #19, You might want to read my post above, it contains the words, "GRACE and GPS" as well as "Khan, S. A., J. Wahr, M. Bevis, I. Velicogna, and E. Kendrick" So, I do suspect that they have picked up on using GPS to account for rebound; though, I don't know if they used the same math as Wu.
    0 0
  34. TIS - "There is a good reason to be skeptical about the significance of the current behavior." Uh huh. It appears that you broken second link was actually a meant to be link to your own site. The article I assume is Jakobsson, 2010? You would do your readers a service if you linked to the article. Quote from article - "that Arctic sea ice cover was strongly reduced during most of the early Holocene; there appears even to have been periods of ice free summers in large parts of the central Arctic Ocean". A slightly more cautious assessment than yours perhaps? The article also points out the rather different forcings at work. These forcings are NOT present today which is what makes the ice loss significant. And to hammer home the important point yet again - its the rate of change compared to what happens with natural forcings that is the major concern.
    0 0
  35. Chris G @ 33 - missed that, thanks. I note in the Khan 2010 paper abstract, that they have now deployed far more permanent GPS stations around the Greenland coast (now up to 51). Was it 3 that were used in the WU study?. Spread of ice mass loss into northwest Greenland observed by GRACE and GPS "In addition to showing that the northwest ice sheet margin is now losing mass, the uplift results from both the GPS measurements and the GRACE predictions show rapid acceleration in southeast Greenland in late 2003, followed by a moderate deceleration in 2006. Because that latter deceleration is weak, southeast Greenland still appears to be losing ice mass at a much higher rate than it was prior to fall 2003. In a more general sense, the analysis described here demonstrates that GPS uplift measurements can be used in combination with GRACE mass estimates to provide a better understanding of ongoing Greenland mass loss; an analysis approach that will become increasingly useful as long time spans of data accumulate from the 51 permanent GPS stations recently deployed around the edge of the ice sheet as part of the Greenland GPS Network (GNET)."
    0 0
  36. When the story of uplift in Greenland due to ice loss appeared on Yahoo, at least one comment seriously claimed that Greenland was ice free when the vikings arrived.
    0 0
  37. @Don Gisselbeck: yep, that's the danger of some of the 'denialist' memes floating around - they enter the broad body of stuff that "everyone knows", despite being completely (and provably, in many cases) false. This is exactly what makes progress in climate action so difficult.
    0 0
  38. "Greenland temperatures were the hottest on record." Is it possible to qualify this statement? From table GL1 I see lots of records being set in 2010 but mainly only at stations which begin records after 1949 (Nuuk would standout from this). In fact in terms of annual temperature records 1929 and 2005 might also be standout years. The longest records have many records set in the first half of the 20th C. I used KNMI Climate Explorer to plot Greenlands temp record (NCDC). 2005, 2007, 1943, 2008 and 1995 all seem hotter in Greenland than 2010. I think the statement above is a little misleading due to the poor presentstion of the temperature data in the report. It would have been very easy to simply present a temperature record for Greenland as a single line on a graph. If you did that then 2010 would be hot but wouldn't be the standout year suggested in the text. Why didn't they do that?
    0 0
  39. The Inconvenient Skeptic at 02:45 AM on 2 November, 2010 "Another study from September showed that the isostatic adjustment from the last glacial period is causing the ice loss to be overstated by about double. So which is correct? The studies that give the higher results don't take the adjustment into account. Stating that the loss is 200+ Gt/yr as fact when there are “published” articles that give results that are half as much is a bit disingenuous." Do you know what is also disingenuous. Giving the impression you know what you're talking about when you don't. Adjustments for GIA are done to all grace and altimetry methods. This study you refer to (Wu et al. 2010), does it in a different way than before for Grace data. Is it better? Well it disagrees with the three other primary methods Radar interferometry, Altimetry and Previous Grace studies. In fact a new study (Sorensen et al. 2010) evaluates 4 different methods for estimating Greenland's mass balance using icesat's laser altimeter and concludes that the best estimate is 237 GT/year. The point here Mr. Kerr is that just because a study is the newest doesn't mean it is the best. The best way to verify results in science is to use multiple methods to measure ice trends. Another little note for you. Wu et al (2010) shows ice losses at the upper limit of IPCC estimates. I don't know how you skeptics call this good news?
    0 0
  40. HR @38, I think John may have erred when he said "hottest on record". In the report they say: "A clear pattern of exceptional and record-setting warm air temperatures is evident at long-term meteorological stations around Greenland (Table GL1)." They then go on to indicate which stations had record setting seasons (e.g., Nuuk (warmest spring and summer) and Thule (warmest spring), or Aasiaat warmest past 12-months on record). So their summary is, IMHO, a fair reflextion of recent temperatures at stations with long-term records. So, IMHO, John should probably say: "Noteworthy are the exceptional and record-setting warm air temperatures observed over portions of Greenland so far 2010". Caveat--it could be that another data set, such as GISS or ETA-interim, supports John's wording, I don't know.
    0 0
  41. Glenn Tamblyn #14 "Individually we can do nothing, only when we all act together." More realistically, at least have a good plan B in the works. With all those computers and bull dozers, just think of the possibilities... perfect waves for surfing, fish farms, etc.
    0 0
  42. Robert Wray #39: "The best way to verify results in science is to use multiple methods to measure ice trends." Speaking of which; Cryosat recently completed its commissioning phase... so we should soon have another very high quality data source by which to evaluate the Greenland ice mass (among other things).
    0 0
  43. #30 Albatross Can you please refrain from suggesting nefarious goings on concerning these Greenland Ice Sheet (GIS) data? Thanks. Asking the average "skeptic" to argue without hinting at conspiracy is like asking a baseball player to use a swizzle stick instead of a bat. They may downplay or disavow the conspiratorial angle when it's expedient, but when so much scientific evidence points to the same conclusion, conspiracy is ultimately the only coherent, politically effective counterargument available. It doesn't make any sense, and it requires throwing all standards of evidence out the window (including the ones "skeptics" demand for AGW), but without it, they'd be stuck with the argument that thousands upon thousands of incorrect measurements somehow dovetailed to form the false impression of a dangerously warming world. That's not the sort of argument that fires up the base.
    0 0
  44. Like John Kehr pointed out at #26, there is also a recent study which cuts the melting in half. Yet your graph shows a double loss without any explanation why you picked this information over another. At #29: Yeah very significant. With 103+-24Gt loss / year doesnt sound very significant considering Greenland has 2 600 000 Gt of ice. But of course when the plots are zoomed 1300x the original size it seems significant. Note that todays instruments are VERY sharp and just because we find a result on a direction or another it doesnt yet mean squat. If you would print the data on A4 and then plot also the rest of the scale (whole 2 600 000Gt) you would get 273meters of A4's on top of each other. With the current speed it will melt in just 25 000 or so years. And claims of "acceleration" are pointless when coming from people claiming no shorter trends than 30 years is allowed. Now you have just 8 years of data and instantly claim it "accelerating". Thats a very unsound and hasty conclusion.
    0 0
  45. Actually, protestant, no-one has said trends shorter than 30 years are not allowed-all that has been said is that trends shorter than about 15-20 years tend to lack statistical significance. Yet that never stopped the "skeptics" from claiming there was a cooling trend from 1998-2008(even though no such trend existed). However, whenever it suits them, the skeptics are quite happy to drag out "statistical significance" as a means of refuting the trends that don't suit them. Statistically significant or not, even Blind Freddy can look at the graph above & see a downward trend in the Greenland Ice Mass!
    0 0
  46. @ protestant First, we only have only 8 years of good data. You have to take what you can get. Second, the point of the 30 year trend averages in temp data that "people" insist on is that climate varies significantly because of El Nino and other internal dynamics, as well as volcano eruptions. Looking at shorter time series can reveal short-term increases or decreases that are irrelevant to the longterm overall increasing trend. Now, looking at this series(and the CO2 series for that matter) can you really doubt the existence of a trend? There is a very repeatable seasonal signal, but other than that the decrease is virtually monotonic. Finally, I take the point that its hard to know the exact rate at which melting is increasing given the length of this time series, but is it really so unbelievable that melting rate will increase if temperatures get warmer? And while the rate of melting is not something to worry about now in and of itself, the point is that we don't actually want it to get to the point that it does matter. If a doubling of melting has occured over 8 years, that would be troubling to me. It's worth keeping a very close eye on rather than simply dismissing it.
    0 0
  47. #44: "Note that todays instruments are VERY sharp" Yes, GRACE is sharp. But if you know anything about interpreting gravity data, the problem is complicated by isostatic rebound. Hence the differing interpretations -- which are not contradictory. See also the observation made by RH in #28. "Now you have just 8 years of data" Noooo. There's Arctic ice extent data back to 1972; the satellite ice mass data covers the last 8 years. The acceleration in ice loss is clear from extent as well as mass. Use the SkS search function 'Arctic ice loss' for context; the evidence of acceleration is overwhelming.
    0 0
  48. @Protestant In the Arctic report card they also discuss the melt season (see my post at 30). Those data go back to 1979, and show that "Along the southwestern ice sheet, the number of melting days in August has increased by 24 days over the past 30 years". Not far enough back? OK, how about this study by Jiang et al. (2010) , which shows this: That graph shows the GRACE estimates of ice loss from the GIS along with estimates derived using two independent data sets. For example, shows an acceleration of ice loss from GIS over the period 1958-2007. Now most reasonable people would be concerned by the sudden increase in mass loss observed in recent decades and years. It is not deceptive to show all off the available GRACE data, and especially when scientists make the effort to place those observations in context as is shown in the above figure. We do not have to lose all the ice from the GIS for it to be a concern-- that is a classic argumentum ad absurdum. We have set in motion processes that are going to have some very undesirable impacts on future generations. According to Hansen et al. (2007): "Ice sheet demise may occur in pulses as additional ice sheets or portions of ice sheets (e.g. West Antarctica or the South Dome of Greenland) become vulnerable." And "It is difficult to predict time of collapse in such a nonlinear problem, but we find no evidence of millennial lags between forcing and ice sheet response in palaeoclimate data. An ice sheet response time of centuries seems probable, and we cannot rule out large changes on decadal time-scales once wide-scale surface melt is underway. With GHGs continuing to increase, the planetary energy imbalance provides ample energy to melt ice corresponding to several metres of sea level per century (Hansen et al. 2005b)"
    0 0
  49. http://www.skepticalscience.com/confirm.php?u=3541 This is a link to an adjustment of the estimates of ice loss (especially in Greenland), in which the authors say that a more accurate assessment of the change of the baseline rock under Greenland (due to rebound from the last ice age) is locally anomalous, with the effect that ice mass loss from Greenland has been overestimated. Could someone who really understands this post some explanation?
    0 0
    Moderator Response: [Daniel Bailey] Roger, you'll have to fix your URL provided. That one points to you (your Skeptical Science ID). Thanks!
  50. There is no fixed concept of how many data points you need for statistical significance. When you try to relate two data sets where you have reason to believe one is causally related to the other, you need to use two measures:
    • strength of the relationship, measured by correlation
    • significance of the relationship, measured by the t-test of the correlation
    If you use this calculator, you will see that a correlation of 0.9 (very strong relationship) is also highly significant (p = 0.0073) with as few as 6 data points (the smallest number the calculator accepts). You use a one-tailed test a scenario where only a positive or negative correlation is meaningful, not both. On the other hand a correlation of 0.2 with so few data points is not significant (p = 0.352), whereas the same correlation with 100 data points is (p = 0.023). It is not quite this simple: you need to worry about issues like autocorrelation, and your trust in a statistical test is higher if you have a well-tested causal model, but the basic principle is if you have a p-value < 0.05 (95% chance the effect isn't random) your confidence that you have a real effect should be high, and it consequently becomes more interesting to demonstrate why the effect is not real, rather than the converse. You also cannot apply this kind of correlation (Pearson's) to data sets with very different statistical properties, or where the two data sets have different scale intervals (e.g. one is a log scale and the other isn't and you don't expect an exponential relationship).
    0 0

1  2  Next

You need to be logged in to post a comment. Login via the left margin or if you're new, register here.


The Consensus Project Website

THE ESCALATOR

(free to republish)


© Copyright 2025 John Cook
Home | Translations | About Us | Privacy | Contact Us