A Flanner in the Works for Snow and Ice
Posted on 23 January 2011 by MarkR
A new paper by Flanner et al in Nature Geosciences tries to estimate the so called ‘cryosphere albedo feedback’ since 1979. As Earth warms, ice and snow melt and the loss of their shiny, reflective surfaces means more sunlight is absorbed and global warming receives a boost.
The strength of a feedback can be calculated from how much extra heating it adds as temperatures increase; the equations are here. Climate models expect that changes in Northern Hemisphere snow and ice since 1979 should have been a positive feedback of about 0.25 W m-2 K-1 - i.e. for each degree of global warming, the loss of snow and ice means that another 0.25 W of sunlight is absorbed per square metre of the Northern Hemisphere. Globally, and in the long run it’s expected to be 0.2 because there’s less snow in the south and you eventually run out of summer snow to melt.
Flanner et al use satellites to measure the change in shortwave (i.e. sunlight) reflectivity across the Northern Hemisphere from 1979 to 2008.
They find the total amount of cooling that ice & snow provide to the Northern Hemisphere month by month split between sea ice and snow:
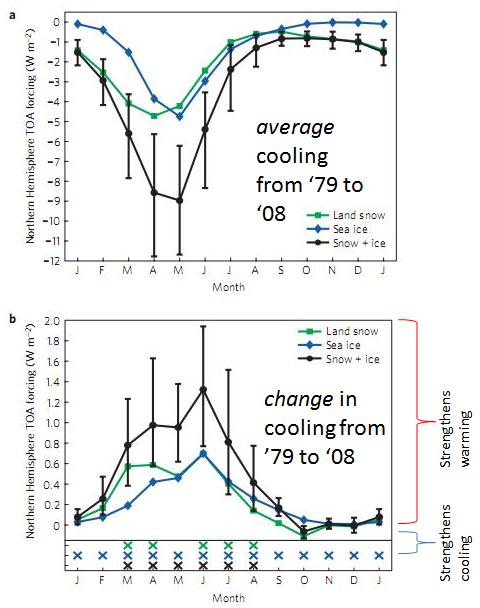
Figure 1 – a) is the total cooling effect by month of snow, ice and snow+ice. b) is the change in cooling effect for each month since 1979 split into snow, ice and snow+ice. Positive means melting has led to more warming, negative means it’s added to cooling.
Even though there is much more ice in the winter, the days are shorter and the sunlight weaker so the total cooling effect is smaller. May to June ice & snow is much more important even though there is less of it. Next they made annual averages and mapped these over the hemisphere:
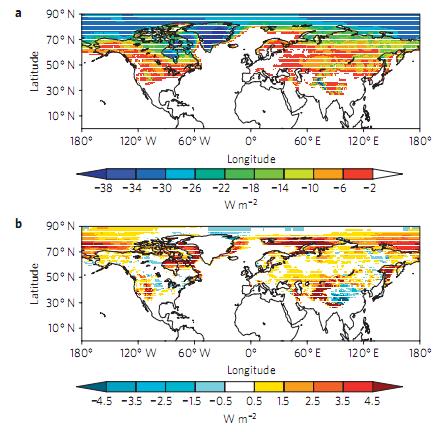
Figure 2 – a) total cooling effect and b) change in cooling effect since 1979 in snow and ice of the Northern Hemisphere.
The authors find that the total effect is 0.33-1.07 W m-2 K-1 with a best estimate of 0.62 W m-2 K-1, significantly higher than climate models’ 0.25 W m-2 K-1. Models have underestimated the darkening of the Northern Hemisphere and therefore how much global warming we’re ultimately in for.
Perhaps the first snow and ice melted more quickly than expected and eventually we’ll run out of the easy to melt bits, or maybe the decline in Arctic sea ice will halt for ~30 years to bring it back in line with models. However, if the current pattern holds then this would boost the best estimate of global warming temperature rises by about 20% - here’s hoping it’s just a blip!































 Arguments
Arguments






























[DB] See for yourself:
[Source]
[DB] Forgot to post the linear relationship details on the chart: R = .94