Measuring CO2 levels from the volcano at Mauna Loa
Posted on 25 October 2010 by Andy Skuce
The observatory near the summit of the Mauna Loa volcano in Hawaii has been recording the amount of carbon dioxide in the air since 1958. This is the longest continuous record of direct measurements of CO2 and it shows a steadily increasing trend from year to year; combined with a saw-tooth effect that is caused by changes in the rate of plant growth through the seasons. This curve is commonly known as the Keeling Curve, named after Charles Keeling, the American scientist who started the project.
Why Mauna Loa? Early attempts to measure CO2 in the USA and Scandinavia found that the readings varied a lot due to the influence of growing plants and the exhaust from motors. Mauna Loa is ideal because it is so remote from big population centres. Also, on tropical islands at night, the prevailing winds blow from the land out to sea, which effect brings clean, well-mixed Central Pacific air from high in the atmosphere to the observatory. This removes any interference coming from the vegetation lower down on the island.
But how about gas from the volcano? It is true that volcanoes blow out CO2 from time to time and that this can interfere with the readings. Most of the time, though, the prevailing winds blow the volcanic gasses away from the observatory. But when the winds do sometimes blow from active vents towards the observatory, the influence from the volcano is obvious on the normally consistent records and any dubious readings can be easily spotted and edited out (Ryan, 1995).
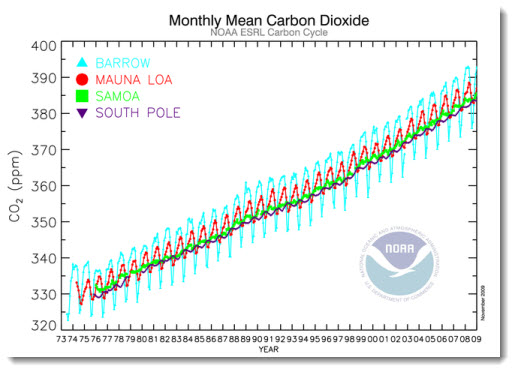
Importantly, Mauna Loa is not the only atmospheric measuring station in the world. As the graph from NOAA shows, other stations show the same year-after-year increasing trend. The seasonal saw-tooth varies from place to place, of course, but the background trend remains steadily upwards. The Keeling Curve is one of the best-defined results in climatology and there really are no valid scientific reasons for doubting it.
Further reading: Spencer Weart's The Discovery of Global Warming describes Charles Keeling's research efforts in more detail. Weart also has a separate article on Keeling's struggle to fund his research.
This post is the Basic Version (written by Andy S) of the skeptic argument "Mauna Loa is a volcano". Note: an advanced version of this argument is in the works and should be published soon.































 Arguments
Arguments






























How do human CO2 emissions compare to natural CO2 emissions?
Water vapor is the most powerful greenhouse gas
What is methane's contribution to global warming?
Claim:
"the prevailing winds are offshore breezes, which bring clean air from high in the atmosphere down to the observatory"
Truth:
This is absolute nonsense. The typical wind currents on the big island are in fact that exact opposite of what you claim. Air currents blow across Kilauea which has been in constant eruption since 1983 and creates a "plume" which has a clear effect on Mauna Loa. So much so that it's created a phenomena called "Vog" that is a major health risk to residents.
http://www.soest.hawaii.edu/met/Faculty/businger/poster/vog/
Andrew LB @25:
1) The active volcano (Kilauea) is located on the South East side of the Island, and South East of Mauna Loa itself. As can be seen below, the prevailing winds at the site of the observatory (on the ridge between Mauna Loa and Mauna Kea) flow from the east, and do not pass over Kilauea. The prevailing winds passing over Kilauea (map area) are to the South West, and carry fumes away from the observatory.
This is illustrated well be the modelled plume for January 26th (of uncertain year), which (as you can see) comes nowhere near the observatory site.
Both of these figures are drawn from the page to which you linked, and show clearly your claim that the observatory is typically affected by the plume is false.
2) The summit of Kilauea is only 1,247 meters above sea level. According to the site to which you linked, the plume affects an altitude "from 151 meters to 2452 meters". This is shown anecdotally by the photo from the site to which you linked, which shows the inversion layer distinctly lower than the summit of Mount Haleakala (3,037 meters). That in turn is significantly lower than the 3,397 meters of the observatory. Doing the maths, we find that the plume typically does not rise to within 940 meters of the observatory. So, once again, your source refutes your claims.
3) The site you link to is an old site, with its first appearance on the wayback machine dating to January 21st, 2003.
Andrew B, even setting aside Tom's maps and analysis, showing that the claim of the Kilauea plume impacting readings at Mauna Loa is fiction... shouldn't the fact that there are not regular large swings in the Mauna Loa data, as winds blow or clear the plume over the observatory, have been enough to see that it was nonsense? Shouldn't the fact that readings at Mauna Loa match those at numerous other sites around the planet have been enough to see that it was nonsense? Shouldn't the fact that thousands of scientists around the world have accepted the accuracy of the Mauna Loa data for decades now, with only random bloggers claiming otherwise, have been enough to see that it was nonsense?
Here's some nice people at NASA helpfully providing additional reasons the claim is bunk;
http://earthobservatory.nasa.gov/blogs/climateqa/mauna-loa-co2-record/
jg recently created a neat graphic showing why Mauna Loa is a very good spot to take CO2 measurements.
The relevant rebuttal "Mauna Loa is a volcano" was updated with it a short while ago. It also includes a cleaned up and improved version of the NOAA-graphic of CO2-concentrations measured in different places of the earth.