Climate Science Glossary

Term Lookup

Enter a term in the search box to find its definition.

Settings

Use the controls in the far right panel to increase or decrease the number of terms automatically displayed (or to completely turn that feature off).

Term Lookup

Term:

Settings

Beginner Intermediate Advanced No Definitions Definition Life:

All IPCC definitions taken from Climate Change 2007: The Physical Science Basis. Working Group I Contribution to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Annex I, Glossary, pp. 941-954. Cambridge University Press.

Home

Arguments

Software

Resources Comments

The Consensus Project

Translations

About Support

	Climate's changed before
	It's the sun
	It's not bad
	There is no consensus
	It's cooling
	Models are unreliable
	Temp record is unreliable
	Animals and plants can adapt
	It hasn't warmed since 1998
	Antarctica is gaining ice
	View All Arguments...

Latest Posts

Archived Rebuttal

This is the archived Advanced rebuttal to the climate myth "Positive feedback means runaway warming". Click here to view the latest rebuttal.

What the science says...

Unlike the simple example of positive feedback we learned in high school, the increase from every round of feedback gets smaller and smaller, in the case of the enhanced greenhouse effect. It is a significant factor in the overall warming, but it doe

One of the problems about understanding the extent of global warming is that the total average temperature increase due to CO₂ is greater than the first guess: Climatologists must also take into account "second-order" effects which amplify the initial estimate of the warming. It is not easy to calculate these effects, but the general consensus is that, overall, they magnify the temperature increase by about a factor of 3. These second-order effects work as a form of "positive feedback."

An example of this: Imagine the pre-industrial world, with the Earth, land & sea, in rough thermal balance. Then add a dollop of 35% more CO₂ to the atmosphere (by burning fossil fuels): Due to the enhanced greenhouse effect (EGE), the outgoing radiation of infrared energy is inhibited, and this reduction in radiative cooling raises the global average temperature. But the increase in temperature has the effect of increasing even further the amount of atmospheric CO₂, because the heated ocean will hold less CO₂ (think of a can of warmed Coke), and the warming Arctic tundra will reveal formerly frozen biomass that will decompose and release more CO₂. So you get even more CO₂ in the atmosphere, which gives rise to even more warming, which gives rise to even more CO₂...

But this is where the suspicions of the skeptics are aroused: "If more CO₂ gives rise to higher temperature, and higher temperature gives rise to more CO₂, and this additional CO₂ gives rise to even higher temperature, doesn't this go on forever? Doesn't that mean that the Earth would turn into an oven? If the greenhouse effect REALLY has positive feedback, why hasn't this happened already? Something is wrong with this picture!"

This line of thought is partly right and partly wrong:

Yes, in a sense this cycle does go on forever; but
No, the Earth will not turn into an oven!

How can these both be true? Well,

The cycle does go on forever, like the reflections between two facing mirrors; but
At each step in the cycle, the incremental increase gets smaller and smaller. After a few cycles, the increase is negligible.

When does positive feedback lead to a "runaway"?

To understand this, consider first the "classic" example of positive feedback: The output of an amplifier is plugged back into its own input. This can lead to a sustained shriek. How does this work mathematically? A simple model: Start at Input level = Io, and call the gain factor g:

- Output = g * Input = g*Io

- Input' = Output = g*Io

and then:

- Output' = g * Input' = g*g*Io

- Input'' = Output' = (g²)*Io

and again:

- Output'' = g * Input'' = (g³)*Io

- Input''' = Output'' = (g³)*Io

and so on...

If you work the math, you can see that Output(n) = (g⁽ⁿ⁺¹⁾)*Io; but another way to figure it out is to use the two equations in a spreadsheet, starting out with Input(1) = Io = 1, with the equations:

Output(n) = g * Input(n)

Input(n+1) = Output(n)

Figure 1 shows the results, for three different values of g: {0.9, 1, 1.2}.

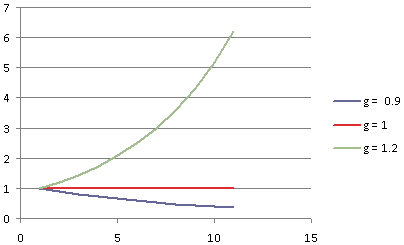
- for g < 1, the value fades exponentially towards 0;

- for g = 1, the value remains unchanged; and

- for g > 1, the value grows exponentially larger and larger ("runaway feedback")

So if the gain factor is > 1, the system is described as "unstable": Any signal grows rapidly out of bounds.

Why doesn't the enhanced greenhouse effect run away as well?

However, this simple understanding doesn't apply to the greenhouse-gas situation, because the equation behind the feedback is different. Let's illustrate this with a highly simplified model: This is inspired by the case of the enhanced greenhouse effect (EGE), but is simple enough that it can be calculated easily. The purpose of this model is to demonstrate that a mathematical system can have positive feedback without necessarily having runaway behavior.

The model is defined by the assumptions below; note that a, b, e, and f are constant values.

- C is the atmospheric concentration of CO₂: We will begin with initial value = 1 (corresponding to 100%).

- dC is the incremental increase in concentration of CO₂: The first dollop of CO₂ will be 0.35 (corresponding to the 35% of increased CO₂ that we have dumped into the atmosphere).

- In general, the radiative forcing due to this dollop dC is

RF = a * d(ln(C)) = a*dC/C

(because the radiative forcing depends on the increase in the logarithm of the CO₂ concentration)

- The incremental increase in global temperature, due to the radiative forcing, is assumed to be:

dT = b * RF = b*a*dC/C

- The resulting 2nd-order increase in atmospheric CO₂ concentration, due to the increase in temperature and the baking out of CO₂, is:

dC' = e * dT = e*b*a*dC/C

(This is just a convenient assumption to make for this toy model.)

Therefore, defining the feedback parameter f = e*b*a:

dC' = f * dC/C

and

C' = C + dC

Just as with the amplifier case, we can use the two equations above to generate a spreadsheet simulation:

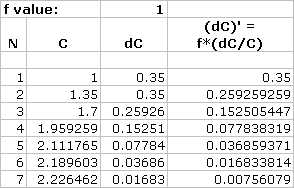
The vertical axis shows the increase of temperature, and the horizontal axis shows the number of iterations of feedback.

Trying three different values of the feedback parameter f, {0.1, 1, 1.2}, and two values for the initial dollop, {35%, 105%}, we see:

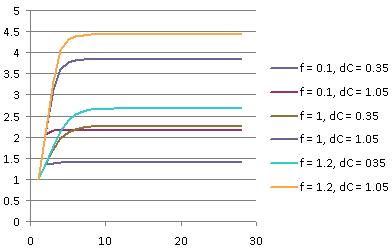
- Due to the feedback, the temperature does indeed rise beyond the initial jump (due to the dollop of CO₂).

- However, after several (3 to 10) iterations, there is no further significant change: It always stabilizes.

- The terminal value of the temperature increase depends on the value of the feedback parameter f: The stronger the feedback, the larger the terminal value; and also the larger the initial dollop, the larger the terminal value.

CONCLUSIONS

- When you add CO₂ to this model, there is indeed positive feedback, so even more CO₂ will end up in the atmosphere than you dumped in from the combustion of fossil fuels.

- However, this does not give rise to a runaway scenario, because the feedback is only logarithmic. Eventually, the impact of that dollop of CO₂ comes to an end.

- Now, in the real world, that end will not be an ultimate end until we stop adding more CO₂ ourselves: Every time we add another dollop of CO₂ from the combustion of fossil fuels, we kick off another round of significant feedback cycles. Currently, we are still adding small dollops all the time...

Note: This model incorporates a number of features of the actual feedback mechanism for the enhanced greenhouse effect, in particular the dependence of radiative forcing on the logarithm of CO₂. However, it is definitely not intended as a full model for the effect. It's only intended to illustrate the point that there is no contradiction for a system to have positive feedback, while maintaining self-limiting behavior.

Note: A more stream-lined presentation of this material can be found here.

Updated on 2010-10-20 by nealjking.

The Consensus Project Website

THE ESCALATOR

(free to republish)

Home | Translations | About Us | Privacy | Contact Us