Arguments
Joseph E. Postma and the Greenhouse Effect
Posted on 17 August 2011 by Chris Colose
Some recent attention has recently been going around the web concerning a new “paper” done by Joseph E. Postma (PDF here) which claims to “…physically negate the requirement for a postulation of a radiative atmospheric greenhouse effect.” It has been echoed particularly by some of the more crackpot web sources like climaterealists.com, and of course is spreading around various "skeptic" blogs.
The claims are of course extraordinary, along the lines of Gerlich and Tseuchner’s alleged falsification of the atmospheric greenhouse effect. As is often the case with these types of “skeptics,” the more extravagant the claim, the more obscure the publishing venue; in this case the host is Principia Scientific International, which according to the website “…was conceived after 22 international climate experts and authors joined forces to write the climate science bestseller, ‘Slaying the Sky Dragon: Death of the Greenhouse Gas Theory.’” Most rational people would stop here, but this is the Americanized age where we need to glorify everyone’s opinion and must provide rebuttals for everything, so here it goes:
I ask that the reader have the paper open in a new window so they can follow along with this article.
The Foundations
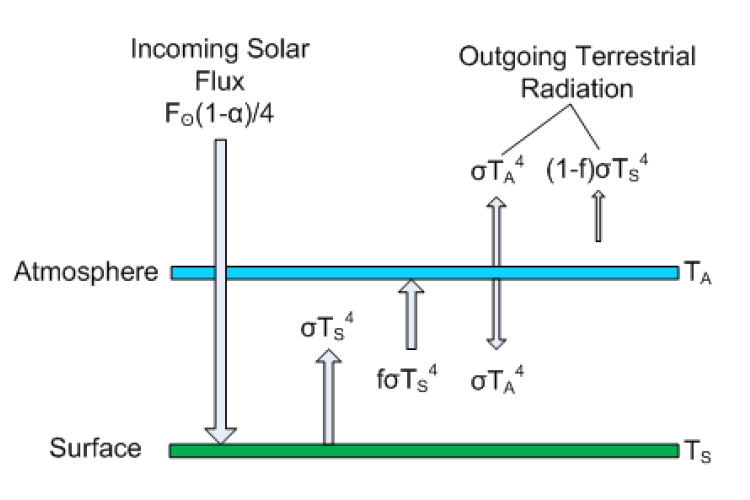
Most of Postma’s first 6 pages are actually correct. He describes the greenhouse effect through the so-called layer model, which is a simple way to break up the planet into a “surface” and an “atmosphere,” with outer space overlying the top layer. This model is described in many climate books such as Dennis Hartmann’s Global Physical Climatology, David Archer’s Understanding the Forecast, Marshall and Plumb’s Atmosphere, Ocean and Climate Dynamics, and radiation books like Grant Petty’s First Course in Atmospheric Radiation. I will say that I do not particularly like this model as a suitable introduction to the greenhouse effect. It is useful in many regards, but it fails to capture the physics of the greenhouse effect on account of making a good algebra lesson, and opens itself up to criticism on a number of grounds; that said, if you are going to criticize it, you need to do it right, but also be able to distinguish between understood physics and simple educational tools.
The atmosphere in Postma’s paper is just a single slab, so he has two layers (atmosphere+surface), but in general you can have many atmospheric layers of varying emissivity. He goes on to solve for the energy balance of each layer (see equations 11-14). RealClimate derived the same result in less than a page here.
Figure 1: Layer model is Postma's paper. Click to Enlarge
Postma actually doesn’t get the atmospheric radiative flux right. The emission is not σTa4, it is fσTa4, where f is the atmospheric emissivity/absorptivity (following his notation). The emissivity is a unitless factor between 0 and 1 descrbing how good of an absorber/emitter the object is relative to an ideal body. f = 1 describes a blackbody. By Kirchoff's law, the absorptivity of a layer must be equal to the emissivity (at the same wavelength), Both right hand sides of equations 11 and 12 are thus wrong, but it turns out that those errors cancel each other out and he gets equation 14 right. The factor of 2 in Equation 12 comes about because the atmosphere emits both up and down, although Postma clearly doesn't know how to derive this result formally, based on later statements he makes about this. Toward the end of page 14 he says this is invalid since the atmosphere radiates in 3-D, not just up and down. In fact, the quantity σT4 refers not only to the total power output of an object (the rate of energy emission), but it also refers to isotropic (equally intense in all directions) radiation. The result σT4 is obtained if one assumes that a plane radiates uniformly over a hemisphere (for example, the domed "half sphere" field of vision that a human can see when you stand outside," with the base of that half-sphere being the surface you sre standing on; the other hemisphere is invisible (see this image).
So far, it is simple textbook stuff with not much promise.
Geometry of the Global Energy Budget
Postma then goes on to describe fictitious “boundary conditions.” In particular, he seems to have serious objections to the averaging of the solar radiative flux over the Earth. In essence, he would prefer we had one sun delivering 1370 W/m2 of energy to the planet, with a day side and a night side, noon and twilight, etc. instead of the simple model where we average 1370/4=342.5 W/m2 over the planet (so that the whole Earth is receiving the appropriate "average" solar radiation). The number becomes ~240 W/m2 when you account for the planetary albedo (or reflectivity).
The factor of 4 is the ratio of the surface area to the cross section of the planet, and is the shadow cast by a spherical Earth. It is therefore a geometrical re-distribution factor; it remains “4” if all the starlight is distributed evenly over the sphere; it is “2” if the light is uniformly distributed over the starlit hemisphere alone; with no re-distribution, the denominator would be 1/cosine(zenith angle) for the local solar flux.
In simple textbook models, we like to prefer explanations that get a point across, and then build in complexity from there (see Smith 2008 for descriptions on a rotating Earth). Of course, students who use this model are probably educated to the point where they know that day and night exist, and certainly GCMs have a diurnal cycle. The radiative calculations are done explicitly by accounting for the temperature distribution and absorber amount that is encountered at each grid box. Postma is simply tackling a non-issue, just as how people criticize the term “greenhouse effect” for not working like a glass greenhouse. Postma objects to teaching this simple model because it is not real. All that is done, however, is to use a brilliant and sophisticated technique, taught only to the geniuses among us, called averaging! And of course, simple models are used in any classroom...it is how we learn.
But, in actuality, the globally averaged solar re-distribution approximation is not bad when we use it to describe the temperature for planets like Earth or Venus. These planets have an atmosphere or ocean that transport heat effectively, especially Venus with virtually no day-to-night or pole-to-equator temperature gradient. The atmosphere and/or ocean help smooth the diurnal temperature difference very well. Therefore, when coming up with a temperature estimate, it is a great first approximation. If you want the local equilibrium temperature for an airless body like Mercury or the Moon (that does not transport heat), then you want to use the no-redistribution or hemisphere only solar factor. This is well-known (see e.g., Selsis et al 2007). On Mercury, there is no heat distribution and very little thermal inertia; before the sunrise the temperature on the surface is somewhere near 100 K (-173 °C) and by noon the temperature on the surface of Mercury rises to about 700 K (427 °C). This may also be relevant for tide-locked planets (very slow rotation since one side is always facing the host star, the other in perpetual darkness). Earth does not experience any such changes of the sort. On Venus, the variability is even less and most of the planet is at around 735 K.
Summary
To summarize Part 1, Joseph E. Postma did not like a simple model of Earth’s radiative balance where we approximate the Earth as a sphere with uniform solar absorption. Of course, this is never done in climate modeling or in more detailed analyses appropriate for scholarly literature, so it is more an exercise in complaining about undergraduate education than an attempt to correct what he calls a “paradigm” in climatology. Nonetheless, the 0-D energy balance model is a useful approximation on Earth when coming up with an average emission temperature (~255 K), since air circulations and oceans tend to even out the diurnal temperature gradient on Earth, in addition to the thermal inertia provided by the system.
In Part 2, I will examine several of the other claims in the paper.
These posts comprise the Advanced rebuttal to Postma disproved the greenhouse effect
Howdy Joe, still trying to slay dragons?
Joe, this is confusing. Figure 3 is correct, reflecting the fact that the inner surface (on the left) will be at a temperature that is 2^-4 times the temperature of the glass surface to the right. That is what thermodynamics says should happen here (in this obviously extremely simplified case).
Whereas your Fig 5 is not in thermal equilibrium. Thermodynamics does not predict fig 5 as a final outcome. You seem to be confused about what thermodynamics says.
And your example in your conclusion is crazy. Your coal engine assumes no other energy flow out of the system so it is not an engine. You are effectively saying that if a system has perfect insulation and we keep adding energy into it it will keep getting hotter. Well duh! But we aren't getting anything useful out of the system like mechanical work. That isn't an engine.
JPostma @148:
From the PDF:
First, while de Saussure's first experiment with a his improved hot box achieved a temperature of 228oF (108.9oC); his second experiment, which with further improvement, achieved a temperature of 230oF (110oC) did so "... even though the weather was not as favorable as during the prior experiment". This more inclement weather for the experiment with the peak temperature shows that you are not entitled to an assumption of ideal conditions. Further, the experiment which achieved 110oC was not conducted on a mountain. Indeed, the mountain he did conduct experiments on (Mount Cramont) is only 2,740 meters high, hardly enough to avoid all, or even most atmospheric absorption.
You can perhaps assume better conditions for Herschell's experiments, but his peak temperature was 240oF (115.6oC), a value sufficiently exceeding your calculated value to refute your hypothesis. Further, his observations were made not higher than Table Mountain (1,085 meters).
In neither case are you entitled to an inflated modern value of the TSI for an experiment conducted in 1767 (or for Herschell's case, the 1830s). Allowing peak modern values, TOA TSI peaks at 1410 W/m^2, but insolation in 1767 or 1830 was well below that peak value:
Finally, we do not need to relly on these old values. Modern hot box cookers with designs inspired by de Saussure's are tested in modern universities. Of particular interest is the testing of the Sudanese design cooker with the external mirror removed, and the internal mirrors shaded so that it most closely resembles de Saussure's design. Under these circumstances, in April and May of 1998, in Delhi, the Sudanise design reached temperatures of 126oC. We can assume bright sunshine, but this was after the Vernal Equinox, form which it follows that TOA insolation was less than the annual average of 1361 W/m^2. Further, we know the experiments to have been performed at or near sea level, so that. Given your calculated theoretical maximum of 110oC given 1415 W/m^2 and no atmospheric absorption, the 126oC observed clearly falsifies your argument.
TSI peaks at 1410, yes, and the difference of the average TSI from now to then is, what, 0.5 W. So, hardly an inflation - use 1409.5 then. The temperatures where they used reflectors to increase the internal flux are not relevant to a test of the greenhouse effect. And the result of 126C without relfectors is still well below the 182C which would be required if the cooker has an IR emitting cover. 126C is also easily within experimental effects such as having absorption occuring on the shaders, geometrical concerns of the device (the cooker isn't a simple plane), etc.
Herschell's 115C is still well within a no-GHE result, as we expect something closer to 182C with a greenhouse effect.
The values you cite are all hovering around a no-GHE result close to the temperature of the insolation-only expectation. Nowhere near the 182C required for a GHE. All a cooker needs to do is to add another cover layer (or more) to increase their internal GHE, and boost their internal temperatures far, far beyond the insolation-only values. None do.
Their cooker even had a double-pane of glass for cover, so the temperature with a GHE should have skyrocketed to above 200C.
JPostma @153,
1) The temperature I quoted for the Sudanese Cooker was that achieved with the external mirror removed and the internal mirrors covered by black papers. Ergo neither contributed to the elevated temperature achieved.
2) The shape of the box is irrelevant given that, with the mirrors covered, their is not method of concentrating the heat in a particular part within the solar cooker.
3) That temperature was achieved in late April or early May. Ergo the TOA insolation at the time was not 1410 W/m^2 but 1362 W/m^2 or less. The actual surface radiation would have been significantly less than that, and probably not more than 1200 W/m^2. The TOA radiation gives a theoretical maximum temperature of 120.5 C if there is no radiative greenhouse effect as per your claims. The actual temperature achieved was 5 C above that, comfortably falsifying your claims.
@154, the temperature should have skyrocketed, as you put it, only if:
a) There was no heat loss through conduction through the sides;
b) There was no heat loss through air escaping;
c) There was no reflectance of Short Wave Radiation from the interior of the box;
d) The glass panes had zero reflectance of Long Wave Radiation; and
e) The glass panes had zero absorptivity of Long Wave Radiation.
All of these conditions are known to be false. Further, the temperature should only have skyrocketed if the actual insolation approached the theoretical maximum, which as the box was near sea level, is also known to be false.
All of this is irrelevant as to whether the Sudanese Cooker experiment (with external mirror removed and internal mirrors covered) refutes your theory, which places a clear upper limit on temperature achieved. That upper limit is exceeded despite the inefficiencies listed above.
Joe
"The temperatures where they used reflectors to increase the internal flux are not relevant to a test of the greenhouse effect."
What has anything you are talking about got to do with testing the greenhouse effect?
The box you describe is so different from the actual processes in the atmosphere that you can draw no conclusion from it. Without the ability to include convective heat transport and the vertical Lapse Rate anything you might do in such a test is rather meaningless wrt the GH Effect.
Joe, Regarding figure 1 from your pdf.
Here is the accompanying text related to that diagram from the original source.
"A simple approach
We can get the above results directly by recognizing that the top
layer of the atmosphere must emit 239.7 W/m2 of infrared radiation
to space (same amount of solar radiation that enters the atmosphere:
what goes in must go out). The bottom layer of the atmosphere
will emit an equal amount downward to the surface of the planet.
Hence, for thermal equilibrium, the surface of the planet must emit
enough radiation to balance not only the amount it receives from the
sun (239.7 W/m2), but also what it receives in the form of downward
infrared radiation from the atmosphere 239.7 W/m2). Hence, its emission
must match 239.7+239.7 = 479.4 W/m2. Applying the Stefan-Boltzmann
law: constant x T 4 = 479.4 W/m2. We thus calculate T = 303 K.
The figure below illustrates this calculation. Contrast it to the figure
above where we assumed no atmosphere, and you will see where
the greenhouse effect comes in."
Your diagram goes here
"The effective temperature we calculate in this manner is much warmer than the actual temperature of the Earth (288 K), because we made a number of simplifying assumptions.
Limitations of this calculation
1) It's assumed that the atmosphere is isothermal. The layer of the
real atmosphere that's most important in terms of the greenhouse
effect is the troposphere, where temperature decreases with height.
Because of this height dependence, the real atmosphere emits more
radiation in the downward direction than in the upward direction (88
units vs. 70 units in Fig. 3-19).
2) It's assumed that the atmosphere absorbs all the outgoing
radiation at all wavelengths in the infrared part of the
electromagnetic spectrum. In reality, the absorption of radiation by
the atmosphere is highly wavelength dependent. At some wavelengths
there's very little absorption and the radiation emitted by the
earth's surface escapes to space, while at other wavelengths it gets
absorbed, reemitted, absorbed and reemitted many times before it
finally escapes. To carry out this calculation accurately it has to
be done wavelength-by wavelength... to capture the fine scale detail
in the spectrum requires literally thousands of calculations
analogous to the one we did in class.
3) Radiative transfer isn't the only process by which energy escapes
from the earth's surface. Conduction of heat and evaporation of water
transfer about twice as much energy from the earth's surface to the
atmosphere as the net upward flux of infrared radiation from the
radiation does. If the temperature distribution on earth were
determined only by radiative transfer (as in this example) the Earth
would be so hot as to be uninhabitable. In this sense the true
'greenhouse effect' on Earth is much larger than the 33 K difference
between the observed surface temperature (288 K) and the effective
radiating temperature (255 K) ascribed to it in your text." (my emphasis)
This diagram is an intermediate stage as part of a teaching exercise in developing an understanding of the GH effect. It most certainly is not a definitive description of the GH effect.
You have built a house of cards from extrapolating a simplification too far.
Glenn Tamblyn @156, the box Postma mentions is the Sudanese Solar Cooker I mentioned @152. The design is essentially the same as a de Saussure hotbox except for the addition of mirrors to compensate for the box not tracking the Sun. In the crucial experiment I discuss, the external mirror was removed, and the internal mirrors blocked so that they have no effect. What remains is a simple variant of a de Saussure hotbox.
These hotboxes are germaine to climate science in that Line by Line Radiative models and the radiation module of GCMs treat the atmosphere as a series of isothermal slabs which partially absorb outgoing shortwave radiation and then reemitt based on the temperature of the particular layer. The idealization of the de Saussure hotbox is also an idealization of that treatment of radiation. Ergo, if the treatment of radiation in the idealization of a de Saussure hotbox is fundamentally in error, so also is the treatment of radiation in Line by Line Radiation models, and the radiative modules of GCMs.
Of course, that begs the question as to why Postma tests his objections against obscure, poorly controlled experiments with hotboxes rather than the detailed comparisons of observations and the outcomes of Line By Line Radiation models, which are a far more direct and apt test:
It also begs the question as to why Postma treats the grey slab models as the IPCC model of the greenhouse effect rather than, as it is, merely a didactic model used to introduce students of atmospheric physics to the maths of radiation models.
Tom
It is true that GCM's treat the atmosphere as a series of slabs in terms of radiative transfer. But they are also modelling fluid flows and evaporation/condensation passing through these layers as well. Essentially mass transfers vertically, transporting energy. With a sufficiently large number of vertical layers - and you need enough layers to approximate the correct optical depth - the temperature differences between each layer are small and thus the net radiative flows low. The convective and latent heat fluxes can be substantial. So the glass box/radiation only model is severely deficient. This result was first shown by Manabe & Muller in 1961.
In the context of the glass slab model Joe has used, we need to imagine that somehow the material of each of the glass layers is also merging and passing through each other - obviously a not very physical situation.
JPostma @148 (2nd point):
In the PDF you show the following diagram, commenting:
What is obvious from this is that you completely fail to recognize that no glass has perfect transmittance of visible light, and thatn no box is perfectly insulated. You are like some creationist pseudoscientist criticizing Newton's three laws of motions as false because (as it happens) in the real world there is friction, air resistance and uneven forces, all of which lead to divergence between experimental and predicted results in the simple models that ignore those complications.
How much of a problem these factors can actually be is seen by looking at the transmitance of modern, 1/4 inch clear glass:
(Source)
Note that while the diagram shows the example for an angle of incidence of 30 degrees, at 0 degrees (ie, perpendicular to the glass) the transmittance is not appreciably better.
Using a spreadsheet I modelled a 5 pane de Saussure Hotbox with 2% reflectance and 2% absorption. The result showed a backplate temperature of 532 K (258oC), with radiances given in the table below:
Layer SW Down SW Absorbed SW Up SW Up SW Down
5 980 20 179 801 801
4 941 19 140 1582 1582
3 904 18 103 2344 2344
2 868 17 67 3088 3088
1 834 17 33 3815 3815
0 0 801 0 4525 0
(* Note that for convenience of calculation, I ignored reflected shortwave radiation going upward. Any inaccuracy of the calculation thereby introduce is more than compensated by the very low values of reflectance and transmittance relative to the actual case.)
That still ignores heat losses, the two primary sources of which will be heat loss from the backplate zone (as the hottest region of the box) and from the top pane (due to ambient airflow cooling the glass). Introducing just a 50 W/m^2 heat loss for just the second factor drops the backplate temperature to 423 K (150oC), with radiances as follows:
Level SW Down SW Absorbed SW Up SW Up SW Down
5 980 20 179 350 350
4 941 19 140 681 681
3 904 18 103 993 993
2 868 17 67 1287 1287
1 834 17 33 1563 1563
0 0 801 0 1823 0
Note carefully that these results were obtained with reflectances just 29% of, and absorptions just 12% of the actual case with commercial glass. Further, the glass available in 1767 to de Saussure and in 1830 to Herschell would have been much worse than even standard glass available today.
From this analysis it is obvious that adding additonal panes of glass will suffer from a severe case of diminishing returns. With commercial grade glass, it is likely that only the first two or three panels will appreciably improve performance.
It also begs the question as to what sort of "scientist" attempts analysis of experimental results by treating them as ideal cases when there are very well known inefficiencies in the actual processes? IMO only pseudoscientists are so intellectually vacuous.
If you are at all honest, you will redo your analyses including transmittance, reflectance and absorption figures for modern glass, and including reasonable estimates of heat loss other than by radiance. Alternatively you will admit your entire analysis has been specious from the get-go.
Glenn Tamblyn @159, I agree. Indeed, I have been quite critical of the use of slab models to explain the greenhouse effect to the public in the past, considering their only useful application the teaching of the maths of climate models. Never-the-less, if the first law of thermodynamics were rescinded sufficiently for Postma's analysis to be correct, there would be no greenhouse effect. Therefore when discussing Postma's absurdities (and other denier critiques along the same line) we need to show where the reasoning is wrong within the context of idealized de Saussure hotboxes, and in several cases (including Postma's) that there analysis depends essentially on treating real world hotboxes as if they were perfectly insulated and the glass was perfectly transparent to visible light, even though it is well known that both assumptions are false (indeed, absurdly false).