The Skeptical Science temperature trend calculator
Posted on 27 March 2012 by Kevin C
 Skeptical Science is pleased to provide a new tool, the Skeptical Science temperature trend uncertainty calculator, to help readers to evaluate critically claims about temperature trends.
Skeptical Science is pleased to provide a new tool, the Skeptical Science temperature trend uncertainty calculator, to help readers to evaluate critically claims about temperature trends.
The trend calculator provides some features which are complementary to those of the excellent Wood For Trees web site and this amazing new tool from Nick Stokes, in particular the calculation of uncertainties and confidence intervals.
| Start the trend calculator | to explore current temperature data sets. |
| Start the trend calculator | to explore the Foster & Rahmstorf adjusted data. |
What can you do with it?
That's up to you, but here are some possibilities:
- Check if claims about temperature trends are meaningful or not. For example, you could check Viscount Monckton's claim of a statistically significant cooling trend at 4:00 in this video.
- Examine how long a period is required to identify a recent trend significantly different from zero.
- Examine how long a period is required to identify a recent trend significantly different from the IPCC projection of 0.2°C/decade.
- Investigate how the uncertainty in the trend varies among the different data sets.
- Check the short term trends used in the 'sceptic' version of the 'Escalator' graph, and the long term trend in the 'realist' version for significance.
Health warnings
As with any statistical tool, the validity of the result depends on both the expertise and the integrity of the user. You can generate nonsense statistics with this tool. Obvious mistakes would be calculating the autocorrelations from a period which does not show an approximately linear trend, or using unrealistically short periods.
Background
Temperature trends are often quoted in the global warming debate. As with any statistic, it is important to understand the basis of the statistic in order to avoid being misled. To this end, Skeptical Science is providing a tool to estimate temperature trends and uncertainties, along with an introduction to the concepts involved.
Not all trends are equal - some of the figures quoted in the press and on blogs are completely meaningless. Many come with no indication of whether they are statistically significant or not.
Furthermore, the term ‘statistically significant’ is a source of confusion. To someone who doesn’t know the term, ‘no statistically significant trend’ can easily be misinterpreted as ‘no trend’, when in fact it can equally well mean that the calculation has been performed over too short a time frame to detect any real trend.
Trend and Uncertainty
Whenever we calculate a trend from a set of data, the value we obtain is an estimate. It is not a single value, but a range of possible values, some of which are more likely than others. So temperature trends are usually expressed something like this: β±ε °C/decade. β is the trend, and ε is the uncertainty. If you see a trend without an uncertainty, you should consider whether the trend is likely to be meaningful.
There is a second issue: The form β±ε °C/decade is ambiguous without an additional piece of information: the definition of uncertainty. There are two common forms. If you see an uncertainty quotes as ‘one sigma’ (1σ), then this means that according to the statistics there is a roughly 70% chance of the true trend lying between β-ε and β+ε. If you see an uncertainty quoted as ‘two sigma’ (2σ), then this means that according to the statistics there is a roughly 95% chance of the true trend lying between β-ε and β+ε. If the trend differs from some ‘null hypothesis’ by more than 2σ, then we say that the trend is statistically significant.
How does this uncertainty arise? The problem is that every observation contains both the signal we are looking for, and spurious influences which we are not - noise. Sometimes we may have a good estimate of the level of noise, sometimes we do not. However, when we determine a trend of a set of data which are expected to lie on a straight line, we can estimate the size of the noise contributions from how close the actual data lie to the line.
Uncertainty increases with the noise in the data
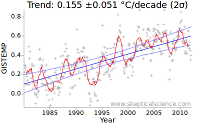
The fundamental property which determines the uncertainty in a trend is therefore the level of noise in the data. This is evident in the deviations of the data from a straight line. The effect is illustrated in Figure 1: The first graph is from the NASA GISTEMP temperature record, while the second uses the adjusted data of Foster and Rahmstorf (2011) which removes some of the short term variations from the signal. The adjusted data leads to a much lower uncertainty - the number after the ± in the graph title. (There is also a second factor at play, as we shall see later.)
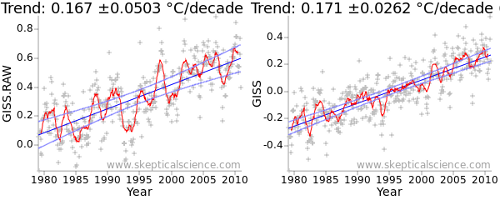
The uncertainty in the trend has been reduced from ~0.05°C/decade to less than 0.03°C/decade.
Note that the definition of noise here is not totally obvious: Noise can be anything which causes the data to deviate from the model - in this case a straight line. In some cases, this is due to errors or incompleteness of the data. In others it may be due to other effects which are not part of the behaviour we are trying to observe. For example, temperature variations due to weather are not measurement errors, but they will cause deviations from a linear temperature trend and thus contribute to uncertainty in the underlying trend.
Uncertainty decreases with more data (to the power 3/2)
In statistics, the uncertainty in a statistic estimated from a set of samples commonly varies in inverse proportion to the square root of the number of observations. Thus when you see an opinion poll on TV, a poll of ~1000 people is often quoted as having an uncertainty of 3%, where 3% = 1/√1000. So in the case of temperature trends, we might expect the uncertainty in the trend to vary as 1/√nm, where nm is the number of months of data.
However a second effect comes into play - the length of time over which observations are available. As the sampling period gets longer, the data points towards the ends of the time series gain more 'leverage' in determining the trend. This introduces an additional change in the uncertainty inversely proportional to the sampling period, i.e. proportional to 1/nm.
Combining these two terms, the uncertainty in the trend varies in proportion to nm3/2. In other words, if you double the number of months used to calculate the trend, the uncertainty reduces by a factor of ~2.8.
Uncertainty increases with autocorrelation
The two contributions to uncertainty described above are widely known. If for example you use the matrix version of the LINEST function found in any standard spreadsheet program, you will get an estimate of trend and uncertainty taking into account these factors.
However, if you apply it to temperature data, you will get the wrong answer. Why? Because temperature data violates one of the assumptions of Ordinary Least Squares (OLS) regression - that all the data are independent observations.
In practice monthly temperature estimates are not independent - hot months tend to follow hot months and cold months follow cold months. This is in large part due to the El Nino cycle, which strongly influences global temperatures and varies over a period of about 60 months. Therefore it is possible to get strong short term temperature trends which are not indicative of a long term trend, but of a shift from El Nino to La Nina or back. This ‘autocorrelation’ leads to spurious short term trends, in other words it increases the uncertainty in the trend.
It is still possible to obtain an estimate of the trend uncertainty, but more sophisticated methods must be used. If the patterns of correlation in the temperature data can be described simply, then this can be as simple as using an ‘effective number of parameters’ which is less than the number of observations. This approach is summarised in the methods section of Foster and Rahmstorf (2011) [Note that the technique for correcting for autocorrelation is independent of the multivariate regression calculation which is the main focus of that paper].
This is the second effect in play in the difference in uncertainties between the raw and adjusted data in Figure 1: Not only has the noise been reduced, the autocorrelation has also been reduced. Both serve to reduce the uncertainty in the trend. The raw and corrected uncertainties (in units of C/year) are shown in the following table:
| Raw uncertainty (σw) | N/Neff (ν) | Corrected uncertainty (σc=σw√ν) | |
| GISTEMP raw | 0.000813 | 9.59 | 0.00252 |
| GISTEMP adjusted | 0.000653 | 4.02 | 0.00131 |
You can test this effect for yourself. Take a set of time series, say a temperature data set, and calculate the trend and uncertainty in a spreadsheet using the matrix form of the LINEST function. Now fabricate some additional data by duplicating each monthly value 4 times in sequence, or better by interpolating to get weekly temperature values. If you recalculate the trend, you will get the same trend but roughly half the uncertainty. If however the autocorrelation correction described above was applied, you would get the same result as with the actual data.
The confidence interval
The uncertainty in the slope is not the only source of uncertainty in this problem. There is also an uncertainty in estimating the mean of the data. This is rather simpler, and follows the normal law of varying in inverse proportion to the square root of the number of data. When combined with the trend uncertainty, this leads to an uncertainty which is non-zero even at the center of the graph. The mean and the uncertainty in the trend both contribute to the uncertainty at any time. However, uncertainties are always combined by adding their squares, not the actual values.
We can visualise the combined uncertainty as a confidence interval on a graph. This is often plotted as a ‘two sigma’ (2σ) confidence interval; the actual trend is likely to lie within this region approximately 95% of the time. The confidence interval is enclosed between the two light-blue lines in Figure 2:
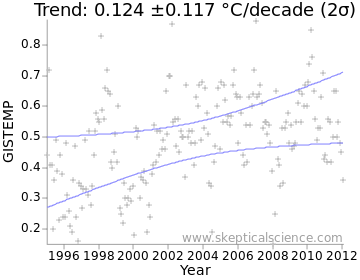
The Skeptical Science temperature trend uncertainty calculator
The Skeptical Science temperature trend uncertainty calculator is a tool to allow temperature trends to be calculated with uncertainties, following the method in the methods section of Foster and Rahmstorf (2011) (Note: this is incidental to the main focus of that paper). To access it, you will need a recent web browser (Internet Explorer 7+, Firefox 3.6+, Safari, Google Chrome, or a recent Opera).
Open the link above in a new window or tab. You will be presented with a range of controls to select the calculation you require, and a ‘Calculate’ button to perform the calculation. Below these is a canvas in which a temperature graph will be plotted, with monthly temperatures, a moving average, trend and confidence intervals. At the bottom of the page some of the intermediate results of the calculation are presented. If you press ‘Calculate’ you should get a graph immediately, assuming your browser has all the required features.
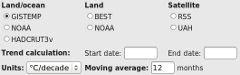
The controls are as follows:
- A set of checkboxes to allow a dataset to be selected. The 3 main land-ocean datasets and the 2 satellite datasets are provided, along with the BEST and NOAA land-only datasets (these are they are strictly masked to cover only the land areas of the globe and are therefore comparable; the land-only datasets from CRU and GISS are not.)
- Two text boxes into which you can enter the start and end date for the trend calculation. These are given as fractional years; thus entering 1990 and 2010 generates the 20 year trend including all the data from the months from Jan 1990 to Dec 2009. To include 2010 in the calculation, enter 2011 (or if you prefer, 2010.99) as the end date.
- A menu to select the units of the result - degrees per year, decade or century.
- A box into which you can enter a moving average period. The default of 12 months eliminates any residual annual cycle from the data. A 60 month period removes much of the effect of El Nino, and a 132 month period removes much of the effect of the solar cycle as well.
If you click the ‘Advanced options’ checkbox, you can also select the period used for the autocorrelation calculation, which determines the correction which must be applied to the uncertainty. The period chosen should show a roughly linear temperature trend, otherwise the uncertainty will be overestimated. Using early data to estimate the correction for recent data or vice-versa may also give misleading results. The default period (1980-2010) is reasonable and covers all the datasets, including the BEST preliminary data. Foster and Rahmstorf use 1979-2011.
If you click the ‘Appearance options’ checkbox, you can also control which data are displayed, the colors used, and the size of the resulting graph. To save a graph, use right-click/save-image-as.
The data section gives the trend and uncertainty, together with some raw data. β is the trend. σw is the raw OLS estimate of the standard uncertainty, ν is the ratio of the number of observations to the number of independent degrees of freedom, and σc is the corrected standard uncertainty. σc and σw are always given in units of °C/year.
Acknowledgements:
In addition to papers quoted in the article, Tamino's 'Open Mind' blog provided the concepts required for the development of this tool; in particular the posts Autocorrelation, Alphabet soup 3a, and Alphabet soup 3b. At 'Climate Charts and Graphs', the article Time series regression of temperature anomaly data also provides a very readable introduction. Google's 'excanvas' provides support for Internet Explorer browsers.
Thanks to Sphaerica, Andy S, Sarah, Paul D and Mark R, Neal and Dana for feedback, and to John Cook for hosting the tool.
Data was obtained from the following sources: GISTEMP, NOAA, HADCRUT, RSS, UAH, BEST.
 For a short-cut, look for the Temperature Trend Calculator Button in the left margin.
For a short-cut, look for the Temperature Trend Calculator Button in the left margin.































 Arguments
Arguments






























Thanks, KR
That's a surprising difference for just three extra years in the a/c calib period.
I'm not sure why, but I now get 1.57+-0.44 C/cen for Had 4 start 1980, default a/c calib (1980-2010), and no change if I switch to 1980-2013 calib.
I'm trying to understand decimal month conventions for entering data. The blog says if you enter 1990, that includes January 1990 data. So if enter 1990 as a start date and 1991 as an end date, I would have 13 months of data, right?
What do I enter to include February data all the way through and including December of a particular year? (11 months of data). One month in decimal form is 0.08. So logically it would seem if I entered 1990.08 as a start and 1990.92 as an end, I would obtain February through and including December data? Help me out here, please.
How often is the data updated? I am curious as we are expecting a warmish year and would like to use the trend calculator to keep up to date with changes in the "no warming meme"
I often use Kevin C’s trend calculator when discussing statistical significance on “skeptic” blogs.
This regularly attracts comments boiling down to the assertion that anything appearing on SkS must be rubbish, although I give reasons as to why I find it credible.
On Jo Nova’s blog Vic G Gallus has provided an argument which is thoughtful and backed by calculations. His argument is that the confidence limits returned by the trend calculator are too large.
I would very much like Kevin’s opinion on this.
Vic has said that he is happy for me to put his case .
Here are some of Vic’s points:
For the GISS data from 2000 using a free product on the web ZunZun (you can use Excel if you have the ToolPack or just type the equations in yourself.) For the function y=Mx+C
C = -1.3189290142200617E+01
std err: 1.90197E+01
t-stat: -3.02426E+00
p-stat: 2.87675E-03
95% confidence intervals: [-2.17979E+01, -4.58064E+00]
M = 6.8552826863844353E-03
std err: 4.72102E-06
t-stat: 3.15506E+00
p-stat: 1.89629E-03
95% confidence intervals: [2.56634E-03, 1.11442E-02]
Coefficient Covariance Matrix
[ 1.34458894e+03 -6.69891142e-01]
[ -6.69891142e-01 3.33749638e-04]
0.07±0.04 °C/decade and not 0.07 ±0.15 °C/decade (FFS)
Using GISS data from 1999, it comes out to be 0.097 ±0.04 °C/decade. I checked the coefficient using Excel and it was 0.097.
A comment from me:
Vic,
I had a suspicion of one possible cause of the differences in the error margin output but thought it would take some time to check on so left it until now, but alas when I go to your links, the first fails and the second is not helpful.
So I will pose this thought:
Looking at the output figures in your post and the blurb on microsoft toolpack:
http://support.microsoft.com/kb/214076
I notice that standard error is mentioned.
The algorithm I am using outputs the error margin as 2 standard deviations, (2σ).
This is the usual marker of “statistical significance”
Note that standard error is smaller than the standard deviation. So a standard error of 0.04 would convert to a 2 sigma value of greater than 0.08.
This would save you from being kicked to death by skeptics who would be outraged at the suggestion that their beloved pause was in fact statistically significant warming, and your GISS value since 1999 of
0.097 ±0.04 °C/decade (one standard error)
would be compatible with that of Kevin C’s algorithm:
Trend: 0.099 ±0.138 °C/decade (2σ)
Vic replies:
Look at the output.
The standard error is stated and it is less than the standard deviation. The latter is not stated but the 95% confidence intervals which equate to 2xSD are.
I have calculated this by putting the equations into Excel as well ( I do not have the ToolPack). The 10-15 year linear regressions for a number of examples and they were in the range 0.04-0.08.
The entire thread begins here:
http://joannenova.com.au/2014/06/weekend-unthreaded-39/#comment-1493093
Looking forward to a response from Kevin.
I suspect at least part of the problem is that the SkS trend calculator correctly takes the autocorrelation of the data into account instead of performing ordinary least squares without this correction. This makes the error bars wider to reflect the fact that there is less information in an autocorrelated time-series than there is in an uncorrelated time series of the same length.
Note the trend calculator gives the following note: "Data: (For definitions and equations see the methods section of Foster and Rahmstorf, 2011)", so if Vic really wants to know what is causing the difference, he should probably start by reading the paper that explains how it works.
See also section titled "Uncertainty increases with autocorrelation" above
Philip Shehan - The difference is indeed, as Dikran points out, due to autocorrelation. The assumptions made in a basic ordinary least squares fit (OLS) such as in MicroSoft Office are of data with uncorrelated white noise, where there is no memory, where each successive value will have a variation defined only by the probability distribution function of that white noise.
Climate, on the other hand, demonstrates considerable autocorrelation, which could be considered as memory or inertia, wherein a warm(cold) month is quite likely to be followed by another warm(cold) month - due to limits on how fast the climate energy content can change. This means that noise or short term variation deviating from the underlying trend can take some time to return to that underlying trend - and not just randomly flip to the opposite value, bracketing the trend.
Therefore determining the trend under autocorrelation requires more data, meaning a higher trend uncertainty for any series than would be seen with white noise. The more autocorrelation is present, the higher the uncertainty, as it becomes less clear whether a deviation is due to some underlying trend change or to a persistent variation.
Again, as Dikran notes, the methods section of Foster and Rahmstorf 2011 describe how the autocorrelation of temperature data is computed and (as described on the calculator page) applied in the SkS trend calculator.
Philip Shehan - I've added a comment on the JN thread to that regard. And noted to Vic Gallus that I've told him this before, only to be ignored.
Thank you Dikran Marsupial and KR.
KR, I saw your comment at Jo Nova and replied there before proceeding here.
If you read the whole thread, you will see that I had my suspicions that autocorrelation was the source of the problem.
I also looked at your links to your previous discussion on Jo Nova.
I too had a sense of déjà vu as you put the arguments about statistical significance and the usual replies. In fact those from "The Griss" were a cut and paste job of the kinds of tirades of abuse he indulges in.
Odd that we have not crossed paths on this before but you like me are probably only an occasional contributor over there. Very nice to have some back up though. It can be very lonely trying to discuss science in a civil manner with the “skeptics” and it requires a very thick skin.
KR,
A final thank you for the very useful information and links provided at J Nova. You may have noticed that a post of mine was snipped by the editor on the grounds that I could not predict the future and that you knew what to expect over there. (Don't we all.)
My prediction was that Bob's up till then polite tone would change if you lept contradicting him.
Sure enough, as your sign off post notes, my prediction was all too predictable.
My response to the editor's comments seems thus far to have been acceptable as it is still there as I type.
Should I receive any more grief on "skeptic" blogs about my use of the trend calculator, I will provide a link containing your analysis.
I haven't been able to locate the downloadable data for the dataset identified as "HadCRUT4 hybrid". Does anyone have a link?
Initially I thought this might actually be Cowtan and Way, but it doesn't seem to be.
Re my #60, maybe it is Cowtan & Way after all. I was only familiar with the long-term dataset, the one that uses kriging.
Is "HADCRUT4 hybrid" actually C&W's HadCRUT4-UAH hybrid?
Kevin C,
Perhaps a note could be added up front mentioning when the Calculator data will be updated. It appear that the plan is to update the Calculator when the full sets of data are available for a calendar year. A question was recently asked on the "Mercury Rising:2014 ..." OP.
Kevin C,
Is there any way to change the scale values on the x-axis to be more representative of the 12 months of data points in a year, like 13.25, 13.50, 13.75?
Kevin C,
Ignore @ 62. I had forgotten to input 2015 as the end year to get the latest data.
Kevin C. ignore my @ 63. This would only matter when looking at short sets of data so it is not relaly relevant.
Have been getting all sorts of grief over at Bolt for pointing out a number of problems with "skeptics" use of temperature data, and using the trend calculator for this purpose.
I am told that I should contact directly the people whose interpretation I criticise and offer tham right of reply. Just like the "skeptics" do with scintistrs they bucket on blogs. (Yes, sarcasm.)
Actually I have on occasion have failed to do so in the case of Fred Singer, David Whitehouse and Patrick J. Michaels, Richard S. Lindzen, and Paul C. Knappenberge
I have told one critic, on numerous occasions that i have checked the trends with those produced by , among others, Monckton, McKitrick, and those who leapt on Jones' "admission" that a 15 year warming trend was not statistically significant, but nearly so, and the trend calculator results match theirs. I have also explained repeatedly the necessity for autocorrelation to be used with temperature data and referred him to this link.
Yet he wrote today.
The calculation that he [that is me] uses is a method written by a shill that just doesn’t make sense and comes out two to three times larger than you would get if you treated the noise as just random.
I will encourage him to represent his argument here.
But thank you for this valuable tool
Of interest this week are the following posts of mine;
On Anthony Watts blog, Patrick J. Michaels, Richard S. Lindzen, and Paul C. Knappenberger dispute a recent paper by Karl et al which questions whether there has been a “hiatus” in global warming.
This new paper, right or wrong, does not affect my primary argument on claims of a “hiatus”.
Which is that such claims do not meet (in fact do not come within a bulls roar of) the criterion of statistical significance.
What is of interest is that the criticisms of Michaels, Lindzen,and Knappenberger again demonstrate the way that skeptics apply totally different standards of statistical significance depending on how they want to spin the data.
The critique of the paper says:
“The significance level they report on their findings (0.10) is hardly normative, and the use of it should prompt members of the scientific community to question the reasoning behind the use of such a lax standard.”
True, the usual standard of statistical significance is the 0.05, 95% or 2 sigma level. The 0.10 level means that there is a 90% probability that the trend is significant
Yet further on Michaels, Lindzen,and Knappenberger claim:
“Additionally, there exist multiple measures of bulk lower atmosphere temperature independent from surface measurements which indicate the existence of a “hiatus"…Both the UAH and RSS satellite records are now in their 21st year without a significant trend, for example.”
Here are the trends for UAH, RSS and Berkeley data (the most comprehensive surface data set ) from 1995 at the 0.05 level
0.124 ±0.149 °C/decade
0.030 ±0.149 °C/decade
0.129 ±0.088 °C/decade
The Berkeley data shows statistically significant warming trend, as do 5 other surface data sets, with mean trend and error of
0.122 ± 0.093 °C/decade
So, Michaels, Lindzen, and Knappenberger object to statistical significance at the 90% level used by Karl et al.
Yet they base their claim of “multiple measures of bulk lower atmosphere temperature independent from surface measurements which indicate the existence of a “hiatus” on two data sets which have a probability of a “hiatus” or a cooling trend of 4.8% (UAH) and 34.5% (RSS).
I mean, these people have the chutzpah to write “the use of [a confidence level of 90%] should prompt members of the scientific community to question the reasoning behind the use of such a lax standard” yet pin their case for a “hiatus” on such a low statistical probability for two cherry picked data sets.
Here is another (Sorry if I am a little robust in my comments here, but I get tired of the abuse over thereand unfortunately respond in kind):
I thought that the entirely inconsistent use of statistical significance by Michaels, Lindzen, and Knappenberger to suit their argument was bad enough, but Singer’s performance here is utterly amazing.
Singer objects to non satellite data “with its well-known problems”.
OK. Lets restrict ourselves to satellite data then:
Here are the graphs for UAH and RSS respectively. [Links to Wood for trees graphs in the original]
Since 1979
0.139 ±0.065 °C/decade
0.121 ±0.064 °C/decade
Statistically significant warming trends in agreement with the non satellite data.
Singer writes:
“the pause is still there, starting around 2003 [see Figure; it shows a sudden step increase around 2001, not caused by GH gases].”
2003
0.075 ±0.278 °C/decade
-0.031 ±0.274 °C/decade
So UAH shows a slight warming trend and RSS shows a slight cooling trend but unsurprisingly, for a 12 year time frame, you can drive a bus between the error margins.
As for the step claim. Nonsense, aided by selecting a colour coded graph that foster that impression. No more a step than plenty of other places on the non-colour coded graphs.
And note the excellent correlation between temperature and CO2 rise for the statistically significant section of the graphs. (And please, spare me the ‘correlation is not causation’ mantra. I know. Singer is talking about correlation.)
He then turns to this period:
1979-2000
0.103 ±0.163 °C/decade
0.145 ±0.158 °C/decade
Warming trends, though not statistically significant.
Now I just have to comment on the text here:
“Not only that, but the same satellite data show no warming trend from 1979 to 2000 – ignoring, of course, the exceptional super-El-Nino year of 1998.”
Gobsmacking.
“Skeptics” have been cherry picking the exceptional el nino of 1998 to base on which to base their “no warming for x years” claim for years.
But because it does not suit his argument, Singer wants to exclude it here.
Then Singer decides that non-satellite data is kosher after all because it suits his argument.
How can he pull this stuff without a hint of shame?
And this guy is supposed to be a leading “skeptic”.
Philip Shehan - "Have been getting all sorts of grief over at Bolt..."
Link?
KR @68.
It is here.
Of course the numpties there have yet to feed the period 1979-95 into the SkS trend calculator to demonstrate that even prior to the famous faux pause, the warming was also statistically insignificant, thus completing their myth-making.
I am myself employing the SkS trend calculator sparing with a numpty at CarbonBrief, one of may denialists that invaded the site to comment on their Karl et al. item. Mine insists most strongly that HadCRUT4 2003-2015.04 is almost statistically significant at 1%. There's always one!
KR
Tree recent and rather lengthy analysies are on these pages. I post as
"Dr Brian" over there when discussing matters of science.
I had to stop using my real name over there for a while for reasons which do them no credit and posted as Brian, my first given name - Philip is my middle name.
I started using the "Dr" for science matters when I became tired of responding to comments along the lines of "Clearly you know nothing about science/mathematics/statistics/ Popper/etc/etc/etc with "Well actually I do... This of course only annoys the “skeptics” more - "Oooooooh you're so arrogant." Which is another reason to keep using it.
But I digress.
I was challenged to refute an argument by David Whitehouse (sorry, not sure how to do links here):
LINK
The two items noted above are at
LINK
and
LINK
Any feedback on the validity or otherwise of my analysis appreciated.
[PS] fixed links. Use the link button (looks like a chain) in the comment editor.
[RH] Shortened links that were breaking page formatting.
Pardon the typos in my comments. dashing things off in beween dealing with more pressing matters.
Philip Shehan - Sorry to say, but I really don't have the spare time to read through four pages of comments mostly consisting of denial. Some points of interest based on what you've shared:
Furthermore, in the statistical theme, here's something I've said before.
Examining any time-span starting in the instrumental record and ending in the present:
Thanks for the comments KR. Fully understand that you are too busy to deal with theose long posts . (And thank you moderator).
A summary then:
The problem with Whitehouse (first link) is that he basically says that non statistically significant warming translates to evidence for a "pause."
This is acommon argument I get from "skeptics".
Their argument is that less than 95% (actually 97.5%, as half the 95% confidence limits are on the high side) probabiility of a warming trend equates to evidence of no warming trend.
Whitehouse also wants to exclude the years 1999 and 200o from trends on these grounds:
“It occurred immediately after the very unusual El Niño of 1998 (said by some to be a once in a century event) and clearly the two subsequent La Niña years must be seen as part of that unusual event. It would be safer not to include 1999-2000 in any La Niña year comparisons.”
To which I commented:
Whitehouse thinks it is entirely kosher to start with the el nino event of 1998 in a trend analysis and presumably include the years 1998 and 1999 in that trend, [ to justify a pasue claim] but you must not start with the years 1999 and 2000. [Starting at 1999 for UAH data gives the same warming trend as for the entire satellite record. Not statistically significant. "Only'' a 94.6% chance that there is a warming trend from 1999. ]
Is it only me who finds this gobsmacking?
I also wrote
[Whitehouse] says “Lean and Rind (2009) estimate that 76% of the temperature variability observed in recent decades is natural.”
No. On the graph itself it states that the model including natural and anthropogenic forcings fits the data with a correlation coefficient r of 0.87.
And the Figure legend says that “Together the four influences [ie natural and anthropogenic] explain 76% r^2 [0.87 x 0.87] of the variance in the global temperature observations.”
Patrick J. Michaels, Richard S. Lindzen, andPaul C. Knappenberger (second link) write of the recent paper by Karl et al:
“The significance level they report on their findings (0.10) is hardly normative, and the use of it should prompt members of the scientific community to question the reasoning behind the use of such a lax standard.”
Yet further on Michaels, Lindzen,and Knappenberger claim:
“Additionally, there exist multiple measures of bulk lower atmosphere temperature independent from surface measurements which indicate the existence of a “hiatus"…Both the UAH and RSS satellite records are now in their 21st year without a significant trend, for example.”
Here are the trends for UAH, RSS and Berkeley data (the most comprehensive surface data set ) from 1995 at the 0.05 level
0.124 ±0.149 °C/decade
0.030 ±0.149 °C/decade
0.129 ±0.088 °C/decade
So, Michaels, Lindzen, and Knappenberger object to statistical significance at the 90% level used by Karl et al.
Yet they base their claim of “multiple measures of bulk lower atmosphere temperature independent from surface measurements which indicate the existence of a “hiatus” on two data sets which have a probability of a “hiatus” or a cooling trend of 4.8% (UAH) and 34.5% (RSS).
Again, is it just me or is these double standards here amazing?
Then there is Springer (third link)
Singer objects to non satellite data “with its well-known problems”. and write of RSS data:
“the pause is still there, starting around 2003 [see Figure; it shows a sudden step increase around 2001, not caused by GH gases].”
I note:
UAH 0.075 ±0.278 °C/decade
RSS -0.031 ±0.274 °C/decade
So UAH shows a slight warming trend and RSS shows a slight cooling trend but unsurprisingly, for a 12 year time frame, you can drive a bus between the error margins.
As for the step claim. Nonsense, aided by selecting a colour coded graph that foster that impression. No more a step than plenty of other places on the non-colour coded graphs.
Singer also writes:
“Not only that, but the same satellite data show no warming trend from 1979 to 2000 – ignoring, of course, the exceptional super-El-Nino year of 1998.”
Again “skeptics” have been cherry picking the exceptional el nino of 1998 to base on which to base their “no warming for x years” claim for years.
But because it does not suit his argument, Singer wants to exclude it here.
Then Singer decides that non-satellite data is kosher after all because it suits his argument.
I am told that I must bow to the experts here.
Am I crazy or are these people utterly incompetant or dishonest when it comes to statistical significance?
[JH] The reposting lengthy segments of comment threads from another website is discouraged.
Pardon the typos above. It's late.
Philip Shehan - "...It would be safer not to include..."
My my - what I'm seeing there is ad hoc data editing, tossing out inconvenient information until what's left is only the data supporting his position. I would consider that the worst kind of cherry-picking.
If you're looking at data too short for significance, you simply need to look at more data. Michaels and Knappenberger (who are lobbyists) are experts at that sort of rhetorical nonsense. So is Singer (also, essentially, a lobbyist), and Lindzen has a long history of being wrong.
You're not crazy - there's deliberate distortion, misrepresentation, and statistical abuse going on. And those people are experts - at just those tactics. Point to the data and move on; you may never get the last word, but you can get in the meaningful ones.
Karl's paper states: "Our new analysis now shows the trend over the period 1950-1999, a time widely agreed as having significant anthropogenic global warming (1), is 0.113°C dec−1, which is virtually indistinguishable with the trend over the period 2000-2014 (0.116°C dec−1)."
The Temperature trend calculator's "Karl(2015)" option correctly duplicates the first trend (0.113) using start and end date inputs 1950 and 2000, but inputs 2000 and 2015 give a result of 0.118, not 0.116. To obtain the paper's 0.116, a start date of 2000.33 (2000 plus four months) needs to be used along with the 2015 end date. So it's curious that the calculator and the paper agree only if less than a complete year is used at the start of the period.
But this is minor when compared the following problem. Something seems to be seriously amiss with the calculator. A check of Karl's data for the entire period 1950 through 2014 (i.e. with start and end dates 1950 and 2015) produces a trend of 0.131°C dec−1. This simply cannot be correct. With the trends from 1950 through 1999 and 2000 through 2015 being 0.113 and 0.118, how can the trend over the combined periond possibly be as large as 0.131? This doesn't make sense. Or am I missing something obvious?
@cunudiun
It's a bit unintuitive, because we imagine the 1950-1999 and 1999-2015 lines to run end to end. However, when we put them on the same graph, we can see what's happening
@ Tristan
Thanks for clearing that up so quickly! (I was going to try to play with WoodForTrees but mistakenly abandoned the effort when I saw that it didn't have Karl's data.)
With this big gap between the pre- and post-1999 trend lines, why should the presence or absence of a "pause" have depended on making the two slopes the same? But that was the chief talking point about Karl's paper: that it dispatched the "pause" to oblivion by making the two trends match up. That was the thing from Karl's paper that made deniers' heads explode, almost Papally.
Karl: "[T]here is no discernable (statistical or otherwise) decrease in the rate of warming between the second half of the 20th century and the first 15 years of the 21st century." Karl certainly performed a great service by improving the accuracy of the data, and this is a very interesting fact, but it's clear even from your graph based on HADCRUT4 data that there was no pause, even without Karl. Neither trend line, pre- nor post-, captures the big jump in temperature around the great 1998 El Niño, and so an analysis simply by comparing the two trends just ignores this surge.
I'm actually a little embarrassed that I didn't pick up on this without your help, being the author of this Tamino-inspired Monckton takedown: https://a.disquscdn.com/uploads/mediaembed/images/2095/6070/original.jpg
cunudian:
I partly covered the problem with chopping up temperature trends into short pieces to fit skeptic argument was covered in one of my earlier long (apologies to mods) posts above.
Then there is the astonishing manner in whech people like Singer and David Whitehouse include and exclude the extreme el nino event of 1998 to suit their argument.
According to Fred Singer (my Bold):
“Not only that, but the same satellite data show no warming trend from 1979 to 2000 – ignoring, of course, the exceptional super-El-Nino year of 1998.”
Never mind that “skeptics” have been starting with the exceptional super-El-Nino year of 1998 in order to claim a “pause”.
Presumably, Singer accepts that the green line here shows a statistically warming trend.
You must not include the period after December 31 1997 in a shorter period because …well, it would spoil his argument .
Singer can declare that that the purple line shows that there is no warming from 1979 to 2000, as long as you leave out the troublesome data after 1997. (The light blue line shows the inclusion of the forbidden data.)
Furthermore, according to Singer, the data from January 1 1998 onward, (the dark blue line) shows a “pause”. No problem including the el nino event at the beginning of a trend, just not at the end, because…well, it would spoil his argument.
And David Whitehouse says you must not start a trend from 2000, (brown line) because… well, it would spoil his argument too.
But back to Singer. Notice that according to his argument there more of a “pause” before the el nino event than after.
The real absurdity is his claim that there is no warming from 1979 to December 31 1997 and there is no warming from January 1 1998 to the present
But there is warming from 1979 to the present.
Singer’s argument is Alice in Wonderland stuff, achieved by chopping a statistically significant warming trend into two short periods where the noise dominates the signal.
It has been claimed that Karl uses OLS calculation of confidence limits rather than autocorrelated confidence limits used in the skeptical science trend calculator. Anyone have an opinion on this?
Philip Shehan @80.
OLS yields 90% limits less than half that quoted by Karl et al (2015) so the 'claim' was nonsense. The method used is described as "using IPCC methodology" which is also evidently not that used by the SkS trend calculator.
Thank you MA Rodger.
I use the trend calculator all the time for personal research, blogging, challenging dopes and dupes in the denialsphere... It's an invaluable tool, but since your latest update I no longer have a grasp of all the data categories. For example, what's the difference between "land/ocean" and "global"? And who is "Karl," with or without "krig"? I would really appreciate it if you would consider adding a legend to the page to remove any ambiguity/uncertainty.
Looks like the UAH numbers aren't following their revised corrections for diurnal drift... nor the ones made by Po-Chedley.
http://journals.ametsoc.org/doi/abs/10.1175/JCLI-D-13-00767.1
I use the trend calc an awful lot. Hopefully it can get updated again. I think its going to be an ongoing project as methods improve.
Perhaps you'd want two versions of the Satellite information ? Can you persuade Po-Chedley et.al. to rework the satellite data regularly?
Thanks
BJ
[PS] Link activated. Please use the link tool in the comment editor in future.
s_gordon_b @83, I would speculate that the temperature indices have been split into those that include an land/ocean index but do not give full global coverage, mostly due to missing polar regions (land/ocean), and those that use various statistical methods to extend the data set to cover all points on the Earth's surface (global). I would also speculate that Karl consists of the NOAA data set updated for the new ocean dataset as specified in Karl (2015), which would suggest that NOAA represents the unupdated data set, even though the latest version of NOAA does include the update SFAIK. On this understanding, NOAA would relate to Karl the way that HadCRUT3 relates to HadCRUT4.
Tom @85, I agree with your speculations, but continue to wish SkS would spell these things out so there's no room for ambiguity. If I want to post a chart from their calculator to my blog, for example, describing it as "I think this is what the data refers to..." doesn't inspire confidence in me or SkS.
s_gordon_b @86, I agree that it would be nice if it were spelled out explicitly. Having said that, everything produced on SkS is done by volunteers who are not paid for their contribution, and certainly not paid for their time producing material for SkS. (This may or may not apply to pieces published for the Guardian, although if Dana is paid for those pieces, I suspect it is a pittance.) Further, many of the contributors are very busy, having a lot of other demands on their time. Given the volunteer nature of the excercise, we are not entitled to any further expectation on their time. If Kevin C (who I know to be very busy), does not have time to update the post - then that is just how it is. We should just continue to appreciate that he has made so much time available free for out benefit as it is.
So, if he hasn't the time for the update, you can always indicate that you "think this is what the data refers to", but that the volunteers have not had the time to clarrify as yet - linking to this post if need be.
What Tom said - I'm doing 60+ hours most weeks counting crystallography + climate stuff, plus domestic duties.
Also I can't update the applet page here - only the data. Updating the applet needs an intervention from the (also over-stretched) technical people. The version of the applet on my York page is more up to date - it has some tooltips and auto-updating. I don't think I've updated the links though - sorry.
Karl krig is the gridded data from the Karl 2015 paper fed through the C&W version 1 kriging calculation from our paper - i.e. infllling the blended data. I let the calculation work out the kriging range for itself - given that the Karl maps are smoothed, this is slightly overestimated (IIRC 850km - 750 is more realistic). However infilling the blended data rather than infilling separately will also underestimate the trend because part of the Arctic will be filled in from SSTs. I don't know which effect will be bigger, so for now it's just a best guess on what the global Karl data will look like.
I'm still a bit new to R and ARIMA - and I have quite some difficulty in locating where in arima output you actually get those values "1.52+-0.404"
"Nick Stokes at 09:13 AM on 29 August, 2013
KR,
Thanks, I should have looked more carefully at the discussion above. I did run the same case using ARMA(1,1)
arima(H,c(1,0,1),xreg=time(H))
and got 1.52+-0.404, which is closer to the SkS value, although still with somewhat narrower CIs."
I may have problems in getting my input data right - or processing / reading it.. Or both.. :(..
Should those numbers be available from someplace here in this output?
Call:
arima(x = ds_hadcrut4_global_yr_subset$value, order = c(1, 0, 1), xreg = time(ds_hadcrut4_global_yr_subset$value))
Coefficients:
ar1 ma1 intercept time(ds_hadcrut4_global_yr_subset$value)
-0.5092 0.7643 -0.2845 0.0168
s.e. 0.2951 0.2214 0.0351 0.0018
sigma^2 estimated as 0.00739: log likelihood = 35.09, aic = -60.18
ds_hadcrut4_global_yr_subset$value contains - or at least should- yearly averages from monthy anomalies 1980 - 2013..
Thanks!
Okay - I guess that was a bit trivial question.. In the output
I get 0.0168 ==> 0.168 C/decade and s.e. 0.0018 ==> +- 1.96*0.0018 = 0.035 C/ decade which is close to what I get now from calculator here for the 1980-2013 period (using the same for autocorrelation period)
Using sarima(ds_hadcrut4_global_yr_subset$value,1,1,1) based on some ideas in a tutorial I get even more close to that
Need to recheck my input data to find in which detail of my excercise the devil is..
I found the code that Tamino used for their 2011 paper and the way they calculated standard error. Looks like I am now able to replicate quite well the slopes and confidence intervals produced by SkS calculator - at least for those series that are clearly identifiable like Berkeley Land, UAH (5.6), RSS (TLT 3.3), GISSTEMP and HadCRUT4..
Unfortunately I still have some challenges with references like NOAA and Karl 2015 which I was not able to identify unambiguously. What I think they may mean (NCDC V3?) is not as close as I would have hoped for. Furthermore Berkeley global is a challenge for me as there my numbers deviate too much from SkS. It would be extremely helpful if the exact data sources (and last update time) were someplace visibe on the calculator page.
(To avoid issues related to possible missing data point in 2015 I have made my calculations for period January 1979 - December 2014.)
The Karl et al 2015 paper that denier are objecting to is linked to on Tom's post. Another link here.
Full citation:Karl, Thomas R., Anthony Arguez, Boyin Huang, Jay H. Lawrimore, James R. McMahon, Matthew J. Menne, Thomas C. Peterson, Russell S. Vose, and Huai-Min Zhang. "Possible artifacts of data biases in the recent global surface warming hiatus." Science 348, no. 6242 (2015): 1469-1472.
yes, but how do I find that series today and how is it different from NOAA? To my understanding both should be the same since last summer or so? So what is the difference here?
I see that some of my questions have actually been raised and answered already above.. Sorry about that..
Considering that my own calculation essentially has been verified through the replication of Foster & Rahmstorf original numbers, and that I get quite close (about rounding error level) to SkS calculator with "well defined" time series, I think I have no urgent questions anymore.
However, it still would be quite nice to have clear definition of exact data sources used, and the timestamp when SkS calculator has retrieved refreshed datasets. But I well understand the issue with time in a voluteer setup.
UAHv6 has finally been published. Kevin C has updated his temp trend app to include it. Could we have that updated at the SkS app, too?
A year and a half late, but thanks for updating UAH6 to the options.
I was curious exactly how the 12-month averaging is centred. I can figure out how to centre a 13-month average - 6 months either side of the month in question+ the month in qestion. But how is it done with a 12 month average?
I should probably clarfy that my thanks is a year and a half late. The update was done about a day after I made the request.