Has Global Warming Stopped?
Posted on 2 August 2010 by Alden Griffith
Guest post by Alden Griffith, creator of Fool Me Once, a new blog featuring video presentations explaining climate science. This blog post is a written version of his first video addressing the argument 'Global warming has stopped'.
Has global warming stopped? This claim has been around for several years, but received new attention this winter after a BBC interview with Phil Jones, the former director of the Climate Research Unit at the University of East Anglia (which maintains the HadCRU global temperature record).
BBC: Do you agree that from 1995 to the present there has been no statistically-significant global warming?
Phil Jones: Yes, but only just. I also calculated the trend for the period 1995 to 2009. This trend (0.12C per decade) is positive, but not significant at the 95% significance level. The positive trend is quite close to the significance level. Achieving statistical significance in scientific terms is much more likely for longer periods, and much less likely for shorter periods.
Those pushing the “global warming has stopped” argument immediately jumped on this as validation, and various media outlets ran with the story, e.g. “Climategate U-turn as scientist at centre of row admits: There has been no global warming since 1995” (Daily Mail).
Well, what can we take away from Dr. Jones’ answer? He says that the positive temperature trend is “quite close to the significance level” and that achieving statistical significance is “much less likely for shorter periods.” What does all of this mean? What can we learn about global temperature trends from the past 15 years of data?
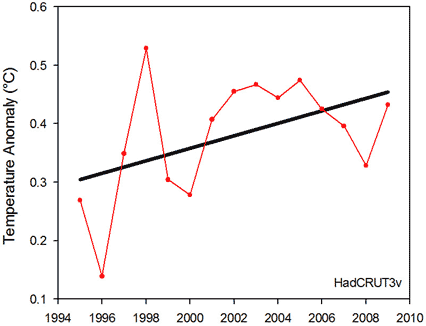
Figure 1: Global temperature anomalies for the 15-year period from 1995 to 2009 according to the HadCRUT3v analysis. The black line shows the linear trend.
First though, it’s worth briefly discussing what “statistically significant” means. This is referring to the linear regression test that informs our decision to conclude whether the slope of the trend line is truly different from zero. In other words, is the positive temperature trend that we observed really any different from what we would expect to see from just random temperature variation? By convention, statistical significance is usually set at 5% (Dr. Jones has simply inverted it to 95%). This 5% refers to the probability that we would have observed such a positive trend if in reality there is no trend. The lower this probability, the more we are compelled to conclude that the trend is indeed real.
Using the dataset available at the time, the statistical significance of the 15-year period from 1995 to 2009 is 7.6%, slightly above 5% (the most recent HadCRU dataset gives 7.1% for this period).
What can we conclude from the statistical test alone? If one was to make any real conclusion, it should probably lean toward there being a positive temperature trend (as the slope is quite close to being statistically significant). We certainly cannot strongly conclude that there’s no trend. Really though, we cannot conclude much at all from such a short time period. Although a 15-year period may seem like a long time, it is relatively short when thinking about changes in climate. So what to do? How can we tell if global warming has stopped or not?
First we need to identify the important questions:
- Do 15 years tell us anything about the long-term temperature trend?
- What temperatures should we expect to see if global warming is continuing?
The first question is essentially putting the skeptics’ logic to the test. The logic is that a 15-year period without a statistically significant trend means that global warming has stopped, or at the very least that it contradicts a warming world. So let’s look further back and see if there are any other 15-year periods without a statistically significant trend:
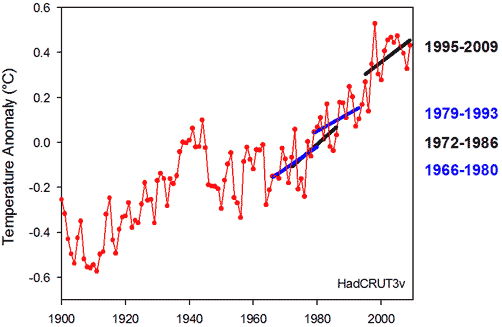
Figure 2: Global temperature anomalies since 1900 according to the HadCRUT3v analysis. The trend lines represent recent 15-year periods without statistically significant warming.
Lo and behold! If we just focus on the most recent period of rapid warming, we see several 15-year periods with trends that are "not significant at the 95% significance level" (actually, since 1965 there are 8 nonsignificant 15-year periods, several of which overlap, and 39 nonsignificant 15-year periods since 1900). So according to the logic, global warming keeps on stopping even though temperatures keep on rising. Clearly this makes no sense! That’s because 15 years of temperature data do not tell us much about temperature trends. Concluding that global warming has stopped from looking at the last 15 years is wishful thinking at best.
The second question is really what we should be asking: What temperatures should we expect to see if global warming is continuing? This is very easy to do. Let’s take the most recent warming trend beginning in 1960 and stop at 1994, just before the last 15-year period. Warming over this period is highly statistically significant (<0.0001%). We can then calculate what’s known as the 95% prediction interval. This gives us the range in which we would expect to see future temperature values if the trend is indeed continuing (i.e. if global warming is still happening at the same rate).
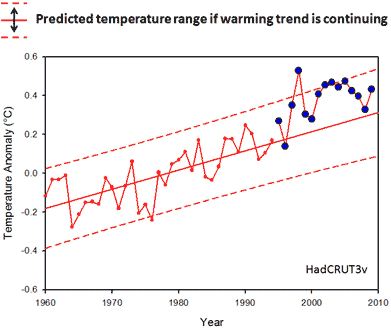
Figure 3: 95% prediction interval (dashed lines) if the linear trend from 1960-1994 is continuing. Temperatures from 1995 to 2009 are plotted in blue.
Lo and behold! The last 15 years are not only within this range, but temperatures are at the upper end of it. In fact, 1998, 2002, and 2003 were even warmer than the predicted range. If you do this analysis for the entire HadCRU time span (1850-2009) you can see that the last 15 years are almost entirely above the predicted range.
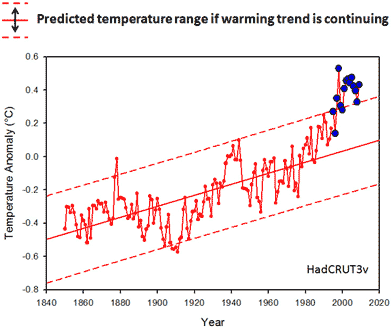
Figure 4: 95% prediction interval (dashed lines) if the linear trend from 1850-1994 is continuing. Temperatures from 1995 to 2009 are plotted in blue.
So here are two requirements for those wishing to conclude that global warming has stopped based on the interview with Phil Jones:
- Accept the backwards logic that allows global warming to keep on stopping while temperatures keep on rising.
- Ignore the real question of whether the last 15 years is consistent with a continued warming trend (which it is).
So no, global warming has not stopped. It takes some serious wishful thinking to say that it has.
[Lastly, I want to make the prediction that global warming will once again “stop” in 2013. Even if temperatures continue to rise over the next 3 years, the 15-year period from 1998 to 2012 will begin with the record setting 1998 El Niño year, which will make statistical significance unlikely. Beware, the return of the “global warming has stopped” argument!]
NOTE: be sure to check out a video presentation of this material at Fool Me Once.
NOTE: This post was updated on 11 Aug 2010.































 Arguments
Arguments























 0
0  0
0 This trend shows a clear decline, with r2=0.4115. The significance of this trend is 99%, much higher than Phil Jones’ linear trend.
Application of a polynomial function to the trend for 1960-2009 gives the following picture. .
This trend shows a clear decline, with r2=0.4115. The significance of this trend is 99%, much higher than Phil Jones’ linear trend.
Application of a polynomial function to the trend for 1960-2009 gives the following picture. . The significance of this trend is very high: r2=0.8448. With 48 degrees of freedom, this has a significance of 99.9% or more. This trend clearly shows a flattening of the warming trend, if not the beginning of a decline.
Saturation functions are much more probable in natural processes than linear functions. Every natural scientist knows, that linear trends never continue ad infinitum!
The significance of this trend is very high: r2=0.8448. With 48 degrees of freedom, this has a significance of 99.9% or more. This trend clearly shows a flattening of the warming trend, if not the beginning of a decline.
Saturation functions are much more probable in natural processes than linear functions. Every natural scientist knows, that linear trends never continue ad infinitum!










Comments