Arctic Sea Ice Loss Has a Larger Impact than Antarctic Sea Ice Gains
Posted on 6 October 2012 by Tamino
This is a partial re-post from tamino's Open Mind blog. For the full post, head over to Open Mind.
In this post, I’d like to compare the albedo feedback between Arctic and Antarctic sea ice changes.
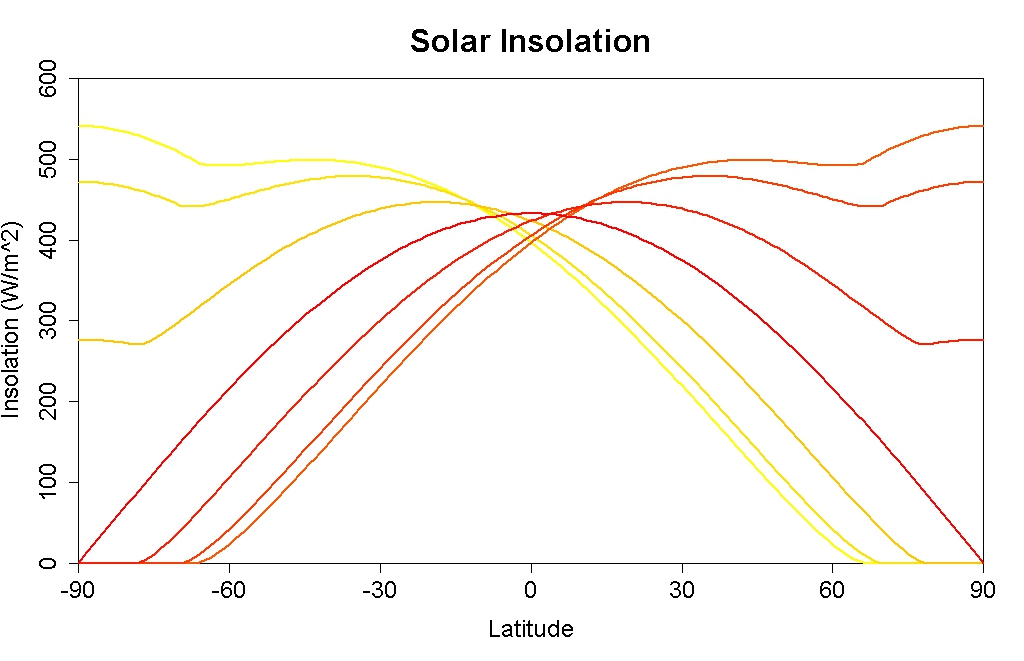
First of all, for most of the year higher latitudes receive less solar energy than lower latitudes. But deep in the heart of summer this is no longer true. In fact at the point of midsummer, the poles receive more solar energy than any other place on earth. Here’s the solar insolation as a function of latitude, for various times of year from northern midwinter (southern midsummer) to northern midsummer (southern midwinter) (note: this does not include the correction for varying earth-sun distance, it’s merely to illustrate the latitude dependence at a given time of year):
During the summer months, when ice albedo feedback really counts, higher latitudes really do get more solar energy than lower latitudes. When the insolation depends strongly on latitude, with higher latitudes getting much less solar energy, the total insolation is so small that the impact of albedo change is small.
Another factor is that earth is farthest from the sun during northern hemisphere summer (when albedo change counts most) but closest to the sun in southern hemisphere summer. That has lead some to believe that the impact of albedo change will be enhanced in the southern hemisphere. This is an understandable mistake; in southern hemisphere summer earth really does receive more solar energy per unit of time because we really are closer to the sun. But the rate of travel of the earth along its orbit is inversely proportional to the square of our distance from the sun — exactly the same proportion by which solar energy changes — so the northern hemisphere summer may be weaker than the southern, but it also lasts longer. For total insolation, the two factors cancel each other so at any given latitude, the annual-total solar energy input is unaffected (a fact which was emphasized by Peter Huybers in relation to ice age cycles). So no, proximity to the sun during southern hemisphere summer doesn’t enhance the ice albedo effect.
If we really want to know the relative impact of ice albedo change between hemispheres, the thing to do is: the math.
I took daily values of sea ice area from NSIDC. I modelled the Arctic ice pack as a circle around the pole of the same area, and the Antarctic ice pack as a ring around the Antarctic continent, with the edge of the Antarctic continent as being at latitude 70S. This is only a crude representation of the geometery of the sea ice packs, but it’s at least correct to first order.
Then I computed, for each day, the sun’s declination (its altitude above or below the celestial equator). I also computed the earth-sun distance so I could apply that correction to the solar insolation. This enabled me to compute the total amount of solar radiation hitting parts of the earth which are covered by sea ice, which I call “sea ice insolation“. I did so separately for the northern and southern hemispheres.
For both hemispheres, sea ice insolation shows a strong annual cycle. So I computed the average total sea ice insolation for each year, for each hemisphere, corrected for earth-sun distance and angle of elevation of the sun. This gives the annual average sea ice insolation in TW (teraWatts). We can then look at the trends in sea ice insolation, to see which pole has lost or gained more in terms of solar energy impacting sea-ice-covered regions.
It’s quite a complicated calculation, so it’s possible I’ve made an error. But the amounts are certainly in the right ballpark, and I’ve done orbital calculations for decades, so I suspect I got it right. The data cover the time span from 1979 through 2011 (2012 isn’t over yet so is not included).
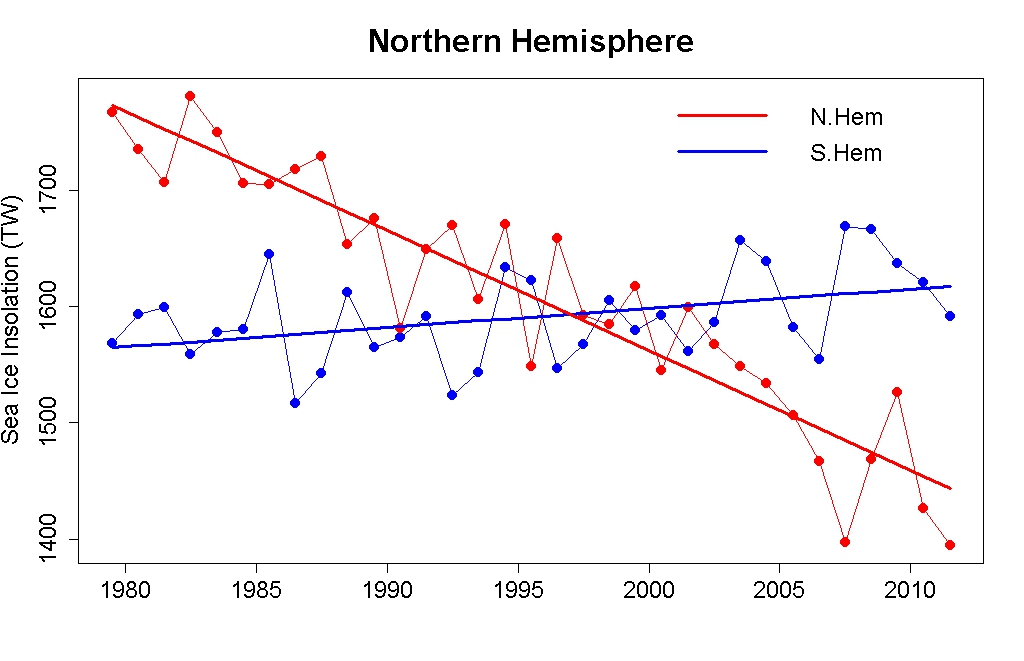
And here’s the result: annual average sea ice insolation, together with linear trend lines, for both hemispheres:
Since 2012 is incomplete, this doesn’t include this year’s ever-so-slightly record high Antarctic sea ice or way-astounding record low Arctic sea ice. But you can see the trends. Clearly. The trend has shown an increase in Antarctic sea ice insolation of about 53 TW, and a decrease in Arctic sea ice insolation of about 329 TW. That’s over 6 times as great.
If we spread 53 TW over the entire earth we get a global average of 0.10 W/m^2. So even if the difference between ice and ocean albedo were equal to 1 in the southern hemisphere (i.e., Antarctic sea ice were perfectly reflective while ocean was completely absorbing) the net global climate forcing would amount to -0.10 W/m^2. But sea ice isn’t perfectly reflecting, not even in the southern hemisphere where the sea ice is often snow-covered, and ocean is not perfectly absorbing. If the top-of-atmosphere (TOA) albedo difference between sea-ice-covered and open ocean areas is 0.2, then the global climate forcing from Antarctic sea ice changes would be about -0.02 W/m^2.
If we spread 329 TW over the entire earth we get a global average of 0.65 W/m^2. If the TOA albedo difference between sea ice and open ocean is 0.2, then the global climate forcing from Arctic sea ice changes would be about +0.13 W/m^2.
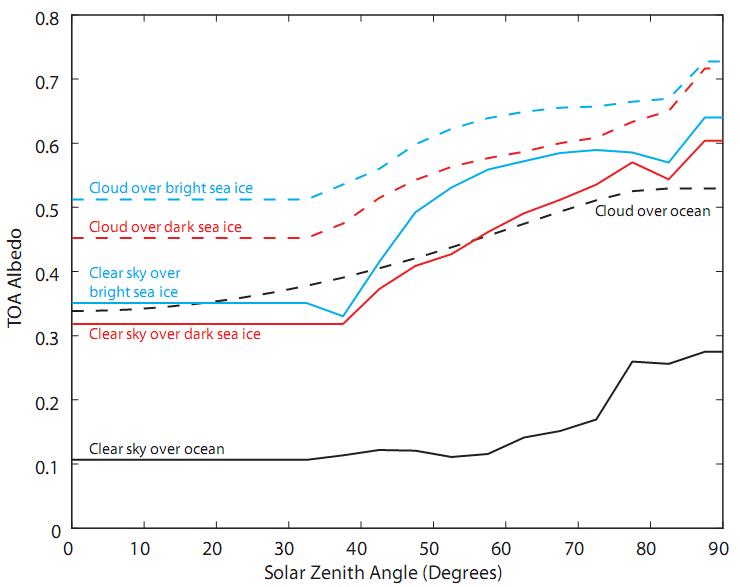
And it turns out that 0.2 is not a bad figure for the TOA albedo difference, according to Hudson (2011):
In fact Hudson states that
"Results show that the globally and annually averaged radiative forcing caused by the observed loss of sea ice in the Arctic between 1979 and 2007 is approximately 0.1 W m-2"
so my crude calculation is certainly in the right ballpark. As I said, this is a pretty complex calculation so I may have made an error, but I certainly ended up in the right neighborhood according to Hudson.
Note: this post has been incorporated into the Intermediate rebuttal to the myth 'Arctic sea ice loss is matched by Antarctic sea ice gain'































 Arguments
Arguments























 0
0  0
0






Comments