Climate Science Glossary

Term Lookup

Enter a term in the search box to find its definition.

Settings

Use the controls in the far right panel to increase or decrease the number of terms automatically displayed (or to completely turn that feature off).

Term Lookup

Settings

All IPCC definitions taken from Climate Change 2007: The Physical Science Basis. Working Group I Contribution to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Annex I, Glossary, pp. 941-954. Cambridge University Press.

Home Arguments Software Resources Comments The Consensus Project Translations About Support

Bluesky Facebook LinkedIn Mastodon MeWe

Twitter YouTube RSS Posts RSS Comments Email Subscribe


Climate's changed before
It's the sun
It's not bad
There is no consensus
It's cooling
Models are unreliable
Temp record is unreliable
Animals and plants can adapt
It hasn't warmed since 1998
Antarctica is gaining ice
View All Arguments...



Username
Password
New? Register here
Forgot your password?

Latest Posts

Archives

Empirical evidence that humans are causing global warming

What the science says...

Select a level... Basic Intermediate

Less energy is escaping to space: Carbon dioxide (CO2) acts like a blanket; adding more CO2 makes the 'blanket' thicker, and humans are adding more CO2 all the time.

Climate Myth...

There's no empirical evidence

"There is no actual evidence that carbon dioxide emissions are causing global warming. Note that computer models are just concatenations of calculations you could do on a hand-held calculator, so they are theoretical and cannot be part of any evidence." (David Evans)

At a glance

Empirical evidence? None? That's a big bold statement to make, so let's take a look. 'Empirical' is defined as something that may be actually measured and presented as a finding. Let's treat the topic as a criminal prosecution. The accused is CO2 and the accusation is that its increased levels through our emissions are warming the planet. As with all court cases, it's important to present an accurate account of events. So firstly, we'll examine the background to this particular case.

It all started in the 1820s, when French physicist Joseph Fourier had worked out that, at its distance from the Sun, Earth should be very cold. He proposed that Earth's atmosphere must contain something that kept the planet warm, like some invisible blanket. His ideas were, it turned out, correct albeit incomplete.

Some decades passed before the nature of Fourier's blanket was discovered. This was done through a series of experiments involving various gases. Interestingly, two investigators worked on it independently, John Tyndall, in the UK and Eunice Foote in the USA. Impressively, their results were virtually identical.

Foote, writing in 1856, was the first scientist to state that carbon dioxide can trap energy. She predicted that if there had been more CO2 in the atmosphere at times past, an increased temperature would have prevailed. That was something the geologists already knew. Tyndall went on to write, in 1861, that on top of carbon dioxide, hydrocarbons - such as methane - would have even greater effects at very low concentrations. The greenhouse effect and its key players had been identified.

The landmark paper, "The Carbon Dioxide Theory of Climatic Change", was published just under a hundred years later. Essentially, it stated what we know now. Without the atmosphere and its greenhouse gases, Earth would be an uninhabitable iceball. As Fourier started to reason all that time ago, greenhouse gases act like a blanket. They keep Earth warm by inhibiting the escape of energy back into space. Humans are adding CO2 to the atmosphere, mainly by burning fossil fuels, thereby intensifying the effect.

That's the background. As we emit more greenhouse gases, the effect is like wrapping yourself in a thicker blanket. Even less heat is lost. So how can we tell that? How can we find hard evidence, like good CCTV footage of our suspect up to their mischief?

How about measuring it?

Satellites orbiting our planet carry sensitive instruments on board. Through them we can measure how much energy is arriving from the Sun. We can measure how much energy is leaving the Earth, out into space. So right there we have two things to compare.

What do the measurements tell us? Over the last few decades since satellites became available, there has been a gradual decrease in the energy heading from Earth's surface back into space. Yet in the same period, the amount of energy arriving from the Sun has hardly changed at all. Something is hanging onto that energy and that something is getting stronger. That something is carbon dioxide - doing exactly as Foote and Tyndall said it would 160 plus years ago.

Verdict: guilty on all counts.

Please use this form to provide feedback about this new "At a glance" section. Read a more technical version below or dig deeper via the tabs above!

Further details

The well-established theory that man-made CO2 is causing global warming is supported as well as any chain of evidence in a rock-solid court case. CO2 keeps the Earth warmer than it would be without it. It has done so for most of geological time. Humans are adding substantial amounts of CO2 to the atmosphere, mainly by burning fossil fuels. Empirical evidence abounds to support the contention that the rising temperatures are being caused by that increasing CO2.

The Earth is wrapped in an invisible blanket

It is the Earth’s atmosphere that makes most life possible. To understand this, we can look at the moon. On the surface, the moon’s temperature during daytime can reach 100°C (212°F). At night, it can plunge to minus 173°C, or -279.4°F. In comparison, the coldest temperature on Earth was recorded in Antarctica: −89.2°C (−128.6°F). According to the WMO, the hottest was 56.7°C (134°F), measured on 10 July 1913 at Greenland Ranch (Death Valley).

Man could not survive in the temperatures on the moon, even if there was air to breathe. Humans, plants and animals can’t tolerate the extremes of temperature on Earth unless they evolve special ways to deal with the heat or the cold. Nearly all life on Earth lives in areas that are more hospitable, where temperatures are far less extreme.

Yet the Earth and the moon are virtually the same distance from the sun, so why do we experience much less heat and cold than the moon? The answer is because of our atmosphere. The moon doesn’t have one, so it is exposed to the full strength of energy coming from the sun. At night, temperatures plunge because there is no atmosphere to keep the heat in, as there is on Earth.

Without the atmospheric greenhouse effect, Earth would be approximately 33°C (59.4°F) cooler than it actually is. That would make most of the surface uninhabitable for humans. Agriculture as we know it would be more or less impossible if the average temperature was −18 °C.

Greenhouse gases act like a blanket, keeping the Earth warm by preventing some of the sun’s energy being re-radiated from Earth's warmed surface, back out into space. If we add more greenhouse gases to the atmosphere, the effect is like wrapping yourself in a thicker blanket: even less heat is lost. So how can we tell what effect CO2 is having on temperatures, and if the increase in atmospheric CO2 is really making the planet warmer?

The heat-trapping effects of CO2 and other greenhouse gases were discovered in the mid-19th century but we can do more sophisticated stuff these days. We can measure the heat energy going into Earth's climate system and that coming back out.

In 1970, NASA launched the IRIS satellite measuring infrared spectra. In 1996, the Japanese Space Agency launched the IMG satellite which recorded similar observations. Both sets of data were compared to discern any changes in outgoing radiation over the 26 year period (Harries et al. 2001). What they consistently found was a drop in outgoing radiation.

This change in outgoing radiation was consistent with theoretical expectations. Thus the Harries paper found "direct experimental evidence for a significant increase in the Earth's greenhouse effect". This result has been confirmed by subsequent papers using data from later satellites (Griggs & Harries 2004, Chen et al. 2007). In the same period, the amount of energy arriving from the sun has hardly changed at all.

When there is more energy coming in from the Sun than there is escaping back out to space, it should come as no surprise to learn that our climate is accumulating heat. The planet's total heat build up can be derived by adding up the heat content from the ocean, atmosphere, land and ice (Murphy et al. 2009). Just since 1998, the planet has accumulated heat energy equivalent to the yield of 3,260,000,000 Hiroshima-sized atomic bombs.

The primary greenhouse gases responsible for the trapping of heat – carbon dioxide (CO2), methane (CH4), water vapour, nitrous oxide and ozone – comprise around 1% of the air. The main components of the atmosphere – nitrogen and oxygen – are not greenhouse gases, because they are virtually transparent to long-wave or infrared radiation.

For our next piece of evidence, we must look at the amount of CO2 in the air. We know from bubbles of air trapped in ice cores that before the industrial revolution the amount of CO2 in the air was approximately 280 parts per million (ppm). In June 2013, the NOAA Earth System Research Laboratory in Hawaii announced that, for the first time in millions of years, the amount of CO2 in the air had gone above 400 ppm. It's now getting on for 420 ppm. That information gives us the next piece of evidence; CO2 has increased by 50% in the last 150 years.

The Smoking Gun

The final piece of evidence is ‘the smoking gun’, the proof that CO2 is causing the increase in temperature. CO2 traps energy at very specific wavelengths, while other greenhouse gases trap different wavelengths. In physics, these wavelengths can be measured using a technique called spectroscopy. Here’s an example:

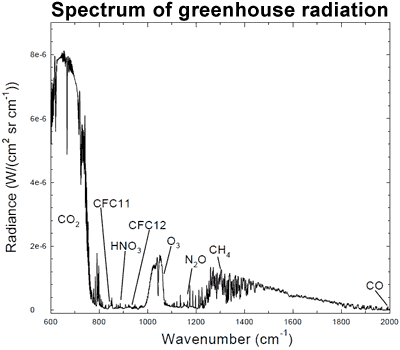
 Greenhouse spectrum

Fig. 1. Spectrum of the greenhouse radiation measured at the surface. Greenhouse effect from water vapour is filtered out, showing the contributions of other greenhouse gases (Evans et al. 2006).

The graph shows different wavelengths of energy, measured at the Earth’s surface. Among the spikes you can see energy being radiated back to Earth by ozone (O3), methane (CH4), and nitrous oxide (N20). But the spike for CO2 on the left dwarfs all the other greenhouse gases, and tells us something very important: most of the energy being trapped in the atmosphere corresponds exactly to the wavelength of energy captured by CO2.

Summing Up

Like a detective story, first you need a victim, in this case the planet Earth: more energy is remaining in the atmosphere.

Then you need a method, and ask how the energy could be made to remain. For that, you need a demonstrable mechanism by which energy can be trapped in the atmosphere, and greenhouse gases provide that mechanism.

Next, you need a ‘motive’. Why has this happened? Because CO2 has increased by nearly 50% in the last 150 years and the increase is mostly from burning fossil fuels.

And finally, the smoking gun, the evidence that proves ‘whodunit’: energy being trapped in the atmosphere corresponds exactly to the wavelengths of energy captured by CO2.

The last point is what places CO2 at the scene of the crime. The investigation by science builds up empirical evidence that proves, step by step, that man-made carbon dioxide is causing the Earth to warm up.

Finally, the myth-creator refers to climate models as "concatenations of calculations you could do on a hand-held calculator". That statement demonstrates nothing more than a limited grasp of what models are and do and is rebutted at this post in our series.

Last updated on 9 July 2023 by John Mason. View Archives

Printable Version  |  Offline PDF Version  |  Link to this page

Argument Feedback

Please use this form to let us know about suggested updates to this rebuttal.

Related Arguments

Denial101x video

Here is a related lecture-video from Denial101x - Making Sense of Climate Science Denial

Comments

Prev  1  2  3  

Comments 51 to 73 out of 73:

  1. Rogerthesurf, the second part of your post-- the section suggesting robust alternative explanations-- is missing.
  2. #35 Riccardo and #49 Ned You have both argued that the issue of observed OLR increasing over the critical period of 79 to end of century (#34 Guinganbresil and #49 Ned) can be dismissed on the hand-waving basis that it is the response to increasing temperatures. However, I do not believe that this can be easily reconciled with CO2 being the primary driver of temperature increase over this period. For an idealised system the OLR perturbation response to a year-on-year geometric growth in CO2 should be a monotonic decrease in OLR upto the equilibration time and a constant (negative perturbation) value thereafter. The constant composition experiments reported in IPCC AR4 suggest an equilibration time of in excess of 80 years in all the models. The models, at least for those whose results I have seen, also get close to a radiative equilibrium in the 70s by using atmospheric aerosols as approximately equal and opposite forcings to CO2 in order to match the temperature decrease in the period 40s to 70s. Hence, if (over the critical 1979 to 1998 period) TSI variation was negligible and there were no other unaccounted forcings, then we would expect to see a decreasing trend in OLR, and not the increase apparently observed. The increase suggests some combination of (a) CO2 effects were overwhelmed by a SW effect (withdrawal of aerosols or decrease in albedo)(b) the planet was releasing stored energy from somewhere into the atmosphere. In any event, it seems to call into question that CO2 was actually the PRIMARY driver over this period.
  3. PaulK, a constantly decreasing OLR correspond to a runaway warming. Luckly this is not the case. The behaviour depends on how fast OLR decreases in the CO2 bands with respect to the increase in the thermal background (proportional to T^4). If CO2 concentration increases at a "pathological" high rate you have a countinuous dcrease of the OLR; this is a runaway warming. If you have, at the other extreme, very slow CO2 increases you get a steady state slightly lower than (almost at) the equilibrium value. In the actual case, you have that CO2 concentration started increasing but the increase of the thermal emission is delayed by it's characteristic response time; so initially OLR decreases but sooner or later thermal emission will try to keep up, untill eventually steady state (not equilibrium) is reached at a value, again, lower than equilibrium. The deviation from equilibrium indicates the rate of increase of the CO2 forcing. In the so called zero dimension aproximation of the atmosphere/surface system this behaviour can be easily modeled. It's worth a try.
  4. John Cook, I suggest that some combination of the contents of Ned's and Riccardo's comments be incorporated in the Is Global Warming Still Happening? post, because the question they are answering arises frequently, and the answer is not intuitively obvious.
  5. As above but with some corrected subscript problems in this version. Riccardo #53 Thanks for the response. I don’t actually disagree with anything you have written, but I believe that you need to follow your conclusions to the next logical step. I wrote initially: “For an idealised system the OLR perturbation response to a year-on-year geometric growth in CO2 should be a monotonic decrease in OLR upto the equilibration time and a constant (negative perturbation) value thereafter.” I think that you are agreeing with this, but let me expand a little. Consider a single ANNUAL pulse of CO2 and an OLR response function in time, f(t), on (0,te), where te is the equilibration time. This function has the properties:- f(t) = 0 at t=0 f(t) <0 for all 0 is less than t is less than te, and f(t) = 0 for all t>=te. Let us define the integral of this function between 0 and t as F(t). The area subtended by the curve at t=te is the FINITE net energy received by the planet as a result of the single year pulse. Call this absolute value Ea. Or we can write F(te) = -Ea. Ea can be related to an increase in the temperature of the planet at equilibrium via the specific heat of the system. For a geometric growth model of CO2, the second year pulse yields an identical response to the first year with an energy commitment of Ea, and the third year is the same as the second and so on. In fact, each year we are adding the same energy commitment, for as long as the geometric growth continues. Now consider the multiyear solution obtained by stacking (superposing) the single year solutions. The stacked solution for OLR approximates to F(t) for t is less than te and becomes a constant negative Ea thereafter. (This is an algebraic identity. I won’t prove this here, but you can confirm it numerically for yourself on a spreadsheet in a matter of minutes.) This is not “runaway” warming. It corresponds to a linear increase in planetary temperature after time te - exactly what one would expect given a logarithmic relationship between CO2 and equilibrium temperature and a geometric growth in CO2. Note also that since f(t) all sits on one side of the zero line, the integral form F(t) is MONOTONIC decreasing (or increasing in a negative direction) irrespective of the choice of functional form for f(t). In the real world, we would not expect to see the monotonic OLR response implied by this solution, but we would expect to see a decreasing trend in OLR if CO2 were the PRIMARY driver of the temperature change - for the reasons I stated in my earlier post. During this period, if CO2 were the primary driver, we therefore should have seen simultaneously a decreasing trend in OLR, a decreasing trend in brightness temperature and an increasing trend in surface temperature. The reason for the opposite signs in brightness temperature and surface temperature come from the increase in downwelling radiation from the continuously added CO2. I do not believe that one can argue (as you seem to) that thermal emissions have overtaken the effects of CO2 on OLR and at the same time that CO2 is the PRIMARY driver of heating over this period. The two things cannot be readily reconciled and indeed this position probably threatens 2nd Law.
  6. PaulK, the heat balance equation can be solved analytically for a forcing linear in time F=b*t (Schwartz 2007); neglecting feedbacks: DT(t) = b*((t-tau)+tau*exp(-t/tau))/l where tau is the response time (=C/l with C heat capacity) and l is the climate sensitivity. For small deviations from equilibrium, i.e. DT<< Te, the increasing thermal radiation E is proportional to DT, E=c1*DT. If the linear forcing is due to an increasing IR absorption (e.g. exponentially increasing CO2 concentration), the total OLR is: OLR(t) = E - F = c1*DT - b*t which, grouping all the constants together for simplicity, can be written as: OLR(t) = c*((t-tau)+tau*exp(-t/tau))-b*t The first term in the equation above is linear for t>>tau and one can write: OLR(t) ~ (c-b)*t - c*tau ; for t>>tau what governs the slope of the OLR is then the term (c-b) which can be positive or negative. For short times, instead, the slope of the OLR is always negative: d OLR/dt = c*(1-exp(-t/tau))-b*t ~ -b*t ; for small t In a few words, with a linear forcing DT will always increase linearly for time much longer than the characteristic response time of the system while OLR may increase or decrease depending on the strength of the forcing. What I (inappropiately) called runaway warming is when you have a continuosly decreasing OLR.
  7. Riccardo #56 Thanks again. The solution methodology I outlined (superposition) does not have to assume a constant linear forcing with time, but I believe should give an identical analytic answer to Schwartz for this assumption. (I will check this as soon as I have a little time.) Schwartz was roundly criticised as I recall for underestimating tau. The CMIP models have an effective tau in excess of 80 years. If you substitute realistic values in Schwartz's derivative term for a tau of 80 years or greater, you should see a negative gradient over the period 70s to end of century assuming a perturbation from quasi- radiative equilibrium, because over this time period t is much less than tau. This is exactly my point. So why did we see a rising gradient in OLR over this period? Either (a) the CO2 response was overwhelmed by other SW effects over this period (such as decreasing aerosols, decreasing albedo, etc), in which case CO2 was not the primary driver OR (b) there was a planetary oscillatory effect of released energy causing a rise in surface temperature, in which case CO2 was not the primary driver OR (c) that the equilibration period is a lot less than inferred by the IPCC from the AR4 "constant composition" experiments, in which case the climate sensitivty to CO2 has been overestimated OR (d) that there was a historic commitment to a trend of rising OLR following a period of 30 years of decreasing temperatures, in which case the CMIP modeling of quasi radiative equilibrium using aerosol forcing as a matching parameter becomes highly suspect. In any event, it seems to me that one hits a major problem of consistency.
  8. PaulK, in the comment i responded to you were making a general point on the possibility to have an increasing OLR. What I tryed to show in my comment is that it's actually possible. But we cannot go much further than the overall behaviour with such a crude energy balance model. Even assuming its validity, for example, the position of the minimum in the OLR critically depends on the choice of the parameters involved, not just the actual time response of the system. There's no point in pushing a model beyond its limits. As for the details you're asking for, well, you know, it's a travesty that we cannot track the details of the energy flow through the climate system ;). Stay tuned, hopefully climatologists will come out with a solution or at least with a better aproximation to the short time variability issue. P.S. The easiest "solution methodology" of the energy balance equation I think is to transform the differential equation into an integral equation (see here, for example) which is much easier to solve numerically for any arbitrary forcing.
  9. Riccardo, Just a couple of points: 1) I have never had a problem accepting the possibility of OLR increasing (even if CO2 is having some warming effect at the same time). If you re-read my first post again, you will see that my argument is that you cannot have CO2 as the PRIMARY driver of heating from the 70s, and have the OLR response which is critical to that heating overwhelmed by thermal emissions derived from some other unspecified source of heating - unless, that is, some other basic assumptions are wrong. 2) You wrote: "Even assuming its validity, for example, the position of the minimum in the OLR critically depends on the choice of the parameters involved, not just the actual time response of the system. There's no point in pushing a model beyond its limits." I disagree strongly with this statement. For a geometric growth in CO2, the minimum (perturbation) in OLR is always achieved at exactly the equilibration time. This is completely independent of the choice of any other parameters. Small variations away from the geometric model, provided they are fitted to the actual data, will always yield a minimum very close to the equilibration time. This is dictated by simple mathematics and requires only two assumptions: (a) CO2 does not cause planetary cooling at some stage in its affect on the system (but it can be multimodal in its affects) (b) Equilibrium temperature change is linearly proportional to the total heat energy gained/lost by the system (i.e. constant specific heat capacity). If the issue here is that I did not adequately explain the maths behind this, then please let me know and I will be happy to provide a more formal proof of this.
  10. PaulK, my bad, not willing to be bothered by the constants i screwed up everything, or better, i didn't notice that the two constants c and b were the same. For the sake of this retraction, below I'll re-formulate the equations. Strange enough, I'm kind of happy that I did this error because before finding it I could not resolve some inconsistencies of the model results. :) As for the problem at hand, i'd like first to point out what the value of the response time τ should be. In the heat balance model, it is defined as the ratio of the relevant heat capacity (of the oceans, mainly) and the climate sensitivity. The oceans do not have a single response time for sure so we're forced to admit that it is the one relevant to the time span considered. In the Schwartz 2007 paper quoted above he gives numbers between 5 and 16 years based on two different approaches. The former looks definitely too small and is probably due to some error. So, in a time span of a some decades and in the presence of a linear forcing one would exepect a essentially zero OLR slope. A positive OLR slope indicates a negative change the in slope of the radiative forcing and viceversa. Looking at the radiative forcings provided by GISS, there has been a slowing down of the GHG forcing around 1990 which could have produce an increasing OLR. But the OLR data are in my opinion too noisy for any definitive assessment (see for example the annual global averages here). In any case, GHGs can still be (and in fact are) the primary (not the only!) forcing but some other effect may just have slowed down the overall forcing. ======== Correct equations from my comment #56 the temperature change is as before ΔT(t) = β*((t-τ )+τ *exp(-t/τ ))/λ OLR(t) = β *((t-τ)+τ*exp(-t/τ))-β*t for t > > τ : OLR(t) ~ -β*τ d OLR/dt = β*(1-exp(t/τ))-β = -β*exp(-t/τ)
  11. Riccardo, Thanks again. With regard to your second paragraph above, Schwartz produced an updated paper where he re-estimated the climate system response time at 8.5 years. I agree with you that if one accepts this equilibration time (or a similar time) , there is no problem explaining a flat or increasing OLR over the period of interest. On the other hand, this equilibration time is an order of magnitude smaller than that assumed in the IPCC model suite. With respect to the Schwartz formulation, I have two fundamental problems with the underlying assumptions, and need to spend some further time on it. One problem is easy to explain:- the ingoing and outgoing fluxes are both defined at TOA, but the estimate used for outgoing then becomes S-B applied at the SURFACE; since we are interested in transient affects before equilibrium, this introduces an error. The second is more complicated and I really have to spend more time thinking about it, but basically the assumption of a linear change in F with time gives rise to a bizarre animal when we start asking what CO2 profile could bring about such a profile in TOA forcing. A geometric growth model in CO2 goes flat at equilibrium time (F = constant) and temperature then becomes linear with time. To get F to continue to increase after equilibration time requires a doubling of the rate of growth of CO2, and then a quadrupling after twice the equilibration time, and so on. Equally bizarrely, for t < equilibration time, the impulse response function which stacks into a linear relationship between F and t is a Fourrier step or uniform distribution on (0,te), and this does not seem very physical. I will invest a few more neurons.
  12. PaulK, I think that you should think at the response time as a sort of weighted average. There are several processes at play operating at different time scales, from years to several centuries, so it's not well defined. Depending on the time span you're looking at you're testing one or a few of them. I see many problems in using the simple heat balance equation for quantitative analysis. It's nice, simple and useful to understand the general behaviour of the system but, as said before, we should not push it to the quantitative comparison with actual data. To have a linear forcing you need an exponential growth of CO2 concentration (the former is roughly logarithmic with the latter), which is about what we're experiencing now. The result correctly is a constant imbalance and a linear increase in temperature.
  13. Riccardo, I plotted out the GISS model data you referenced, and agree that it shows a small change in the gradient of GHG forcing after 1990. However, even with this small gradient change, the modelled GHG forcing is still MONOTONIC INCREASING, suggesting that, all else being equal, OLR should be decreasing unless overwhelmed by other factors. If we look at the total forcing, we see that it INCREASES over the period fairly steadily if one ignores a couple of spikey excursions associated with volcanic events, but that it is always less than the GHG forcing. Hence, (excluding GHGs) all of the other forcings combined are negative in aggregate effect, and thus reduce the heating effect of the putative GHG forcing. Given this, I would guess that this model run would consistently underestimate observed OLR. But perhaps you have the integrated OLR output from the run to prove me wrong?
  14. PaulK, if the system reached the saturation level of the OLR any change in slope of the forcing, not a reduction, will produce a temporary rising/lowering of the OLR. More, any deviation from perfect linearity of the forcing will produce a trend in OLR as well. The only LW output from climate models i can remember right away is in Forster and Taylor 2006.
  15. Hi Riccardo, As promised, I have considered the Schwartz model in a little more detail and think I now understand where the confusion is arising. You need to consider carefully what the forcing term, F, actually means in the Schwartz 2007 paper, because I think it is misleading you (as it did me before I tried to reconcile my results with Schwartz). Consider Equation 6. The F term here is NOT equal to F(t) = Q-E. (If F = F(t)=constant, the temperature could not asymptote to a constant as t becomes large; temperature would continue to increase linearly with constant F(t). F(t) in reality must decrease to zero over time as equilibrium is restored.) It is clear from this, and also from the definition of climate sensitivity that the F in this equation is actually equal (only) to the instantaneous imposed forcing at time t = 0. Now consider Equation 11 for F = bt. Equation 11 is the solution of the convolution integral for Equation 6. In other words, it is the continuous summation in time of a series of Equation 6 terms in order to stack temperature changes. F = bt therefore can be thought of as the continuous stacking of NEW forcings. Or perhaps easier to visualize, d F/dt = b is the rate at which new forcings are added in time. Since the effect of the forcing added at time t1, say, has declined by tn, the actual net forcing at TOA at time tn is therefore NOT equal to F=b*tn. Once again F = bt is NOT equal to Q-E. In conclusion, your attempts to derive an expression for OLR were based on a misunderstanding of the F term, I believe. Your statement that a linearly increasing net forcing (or linearly decreasing OLR for constant TSI) corresponds to a geometric growth in CO2 is incorrect. However, it would be correct to say that a geometric growth in CO2 would give rise to a constant rate of addition of new forcings and a linearly increasing temperature at t>>tau. To highlight how different these statements are – note that the linearly increasing temperature implies a constant dH/dt i.e. a constant net forcing of Q-E even though the F term in the Schwartz model is linearly increasing!
  16. Riccardo, Thanks for the Forster and Taylor reference. I am still digesting, but it looks as though the GISS models along with all of the other models overestimate LW positive feedback and hence underestimate OLR in the observational period. The information here is not definitive, but sometimes if something looks like a duck and quacks like a duck... Thanks again.
  17. PaulK, actually what you call the "Schwartz model" is just the standard energy balance equation, widely used even in the scientific litterature. I think that you are confusing the equation written for absolute temperature with the one for temperature anomaly. You'll find a step by step explanation in the page i linked before. Indeed, it should be clear from the solution given by Schwartz that he's not solving dT/dt ∝ F(t); after linearization the equation is instead
    dΔT/dt ∝ F(t)−λΔT. My evaluation of the OLR comes from the assumption that the forcing is only due to an increased IR absorption which directly influences the OLR. A linear increasing forcing then comes from an exponential growth of CO2 concentration, given the aproximate but quite reasonable relation F=5.35*ln(C/Co) W/m2 where Co typically is the pre-industrial CO2 level.
  18. Riccardo, Sometimes, if you find yourself in a hole, it pays to stop digging. Your comment is wholly irrelevant to the question of what the F term means in the Schwartz model. Unfortunately, I am starting to suspect that you know that already. The site you referred me to for a "step-by-step explanation" appears to be some sort of junk science site, but in any event it is clear that the author of that site is not well trained in basic science. He is making the same conceptual mistake as you are in misunderstanding what the F term means in the Schwartz model, but he manages to “propagate” the error even further without making any attempt to question his own sometimes silly assertions. I quote from the site: Quote Now suppose that prior to our starting time, climate forcing was constant and equal to zero, and temperature departure was constant and equal to zero. After time t0, climate forcing increased to 1 W/m^2 and stayed there. Then the solution turns out to be: Theta(t) = (1 – exp(-lamda*t/C))/lamda Endquote It is hopefully evident to you that Theta (t), the temperature change from the forcing, must asymptote mathematically from this expression to a constant 1/lamda at large values of t. So now ask yourself the question whether it is possible in terms of first law of thermodynamics to have an imbalance of TOA radiative energy for an infinite time which results in a finite (constant) change in planetary temperature. If you can truly answer yes to this question , then I think that I am going to sign off, since I am wasting my time here.
  19. PaulK, the guy that runs that site is a scientist that regularly publish on climate. If you wish to give up learning some rather simple science or if you think you have a better knowledge than climate scientists, feel free to waste your time elsewhere.
  20. Perhaps it's time to invite Tamino here to work things out w/PaulK? PaulK, you may well end up wasting your time here if you swerve an iota further into such remarks as "junk science", shiny dog whistle though the term may be.
  21. Riccardo, If you show me a mathematical expression that says A=B and then argue that a respected climate scientist says that A= 2B, then I am not likely to be convinced by the argument just because he is a respected climate scientist. My questions and assertions are strictly science-based. I may well be wrong, but someone needs to demonstrate that I am wrong in terms of physics and mathematics - whoever he is. I am asserting (#68) that "the guy who runs that site", respected scientist or not, is making a statement which is demonstrably false in terms of basic physics. It is founded on his misunderstanding of what the F term means in Schwartz 2007. I spent some time in post #65 explaining what the F term does mean to give the Schwartz model (or energy balance model if you prefer) some meaning. It is the stacking of instantaneous impulse forcings. As such F(t) in this model does not equal Q(t) - E(t). The respected scientist assumes that it does, which is what leads him to a statement that is demonstrably false.
  22. Doug-Bostrom, For my part, I would be grateful for you to invite (Dr?) Tamino or anyone else if they can contribute to the science questions raised here. I genuinely do not understand your second sentence. I was using the term "appears to be some sort of junk science site" only to describe the blogsite to which Riccardo referred me, not this site. I used this description because the article on that site appears to contain, well, junk science. And I have no idea what the "shiny dog whistle" metaphor refers to. Please clarify if it is helpful. Otherwise, I would prefer to stick to the science arguments.
  23. Doug, perhaps it's time to let Tamino spend his spare time more productively than these trivialities. ;)
  24. PaulK, I may be wrong but as far as I know Tamino has never been found wrong w/regard to posts he's made on his site. I think if you have sufficient force of your conviction behind you, you ought to hie yourself to Tamino's site, tell him you think he's presenting junk science and is insufficiently trained and then do your best to prove it. You delivered the insult, now you should defend it. You have no earned reputation for reliability whereas Tamino does, so really the onus is on you to establish yourself as a superior intellectual force. Failing that, I don't find your reliance on such remarks as "the author of that site is not well trained in basic science" at all persuasive and you are indeed wasting your time here.
  25. PaulK writes "So now ask yourself the question whether it is possible in terms of first law of thermodynamics to have an imbalance of TOA radiative energy for an infinite time which results in a finite (constant) change in planetary temperature" In reality, if you tried to extend this equation to infinite time, you would have to consider that the 1 W/m^2 forcing would disappear at some point. After that point the temperature will obviously go back down, and the first law of thermodynamics will remain unbroken. As long as we are dealing with timeframes << the lifetime of the sun (as we typically do), the equation is perfectly valid as is.

Prev  1  2  3  

Post a Comment

Political, off-topic or ad hominem comments will be deleted. Comments Policy...

You need to be logged in to post a comment. Login via the left margin or if you're new, register here.

Link to this page



The Consensus Project Website

THE ESCALATOR

(free to republish)


© Copyright 2024 John Cook
Home | Translations | About Us | Privacy | Contact Us