Joseph Postma and the greenhouse effect
What the science says...
Joseph Postma published an article criticizing a very simple model that nonetheless produces useful results. He made several very simple errors along the way, none of which are very technical in nature. In no way does Postma undermine the existence or necessity of the greenhouse effect.
Climate Myth...
Postma disproved the greenhouse effect
"Skeptics hope that Postma’s alternative thermal model will lead to the birth of a new climatology, one that actually follows the laws of physics and properly physical modeling techniques...Postma deftly shows how the systemically tautologous conjecture that is “back-radiative heating” just doesn't add up. We see how climatologists fudged the numbers to make it appear as if Earth actually raises its own temperature by having its own radiation fall back upon it - a conjecture contrary to fundamental physics." (John O'Sullivan)
Some recent attention has recently been going around the web concerning a new “paper” done by Joseph E. Postma (PDF here) which claims to “…physically negate the requirement for a postulation of a radiative atmospheric greenhouse effect.”
The claims are of course extraordinary, along the lines of Gerlich and Tseuchner’s alleged falsification of the atmospheric greenhouse effect. As is often the case with these types of “skeptics,” the more extravagant the claim, the more obscure the publishing venue; in this case the host is Principia Scientific International, which according to the website “…was conceived after 22 international climate experts and authors joined forces to write the climate science bestseller, ‘Slaying the Sky Dragon: Death of the Greenhouse Gas Theory.’” Most rational people would stop here, but this is the Americanized age where we need to glorify everyone’s opinion and must provide rebuttals for everything, so here it goes:
I ask that the reader have the paper open in a new window so they can follow along with this article.
The Foundations
Most of Postma’s first 6 pages are actually correct. He describes the greenhouse effect through the so-called layer model, which is a simple way to break up the planet into a “surface” and an “atmosphere,” with outer space overlying the top layer. This model is described in many climate books such as Dennis Hartmann’s Global Physical Climatology, David Archer’s Understanding the Forecast, Marshall and Plumb’s Atmosphere, Ocean and Climate Dynamics, and radiation books like Grant Petty’s First Course in Atmospheric Radiation. I will say that I do not particularly like this model as a suitable introduction to the greenhouse effect. It is useful in many regards, but it fails to capture the physics of the greenhouse effect on account of making a good algebra lesson, and opens itself up to criticism on a number of grounds; that said, if you are going to criticize it, you need to do it right, but also be able to distinguish the difference between understood physics and simple educational tools.
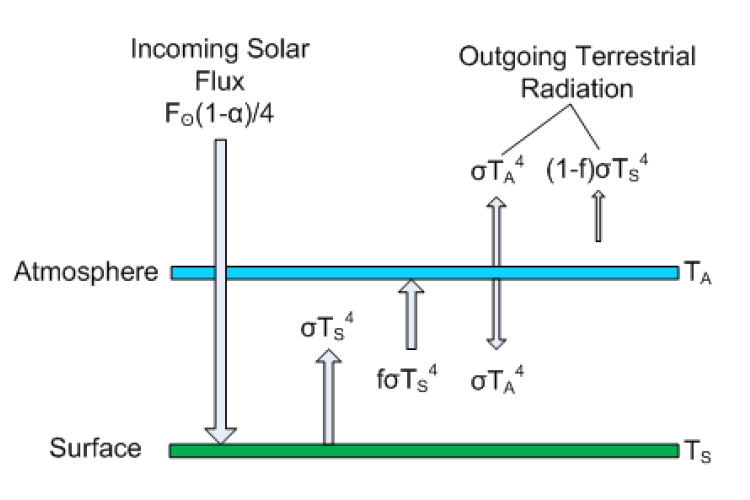
The atmosphere in Postma’s paper is just a single slab, so he has two layers (atmosphere+surface), but in general you can have many atmospheric layers. He goes on to solve for the energy balance of each layer (see equations 11-14). RealClimate derived the same result in less than a page here.
Figure 1: Layer model is Postma's paper. Click to Enlarge
Postma actually doesn’t get the atmospheric radiative flux right. The emission is not σTa4, it is fσTa4, where f is the atmospheric emissivity/absorptivity (following his notation) and Ta is the atmospheric temperature. The emissivity is a unitless factor between 0 and 1 descrbing how good of an absorber/emitter the object is relative to an ideal body. f = 1 describes a blackbody. By Kirchoff's law, the absorptivity of a layer must be equal to the emissivity (at the same wavelength), Both right hand sides of equations 11 and 12 are thus wrong, but it turns out that those errors cancel each other out and he gets equation 14 right. The factor of 2 in Equation 12 comes about because the atmosphere emits both up and down, although Postma clearly doesn't know how to derive this result formally, based on later statements he makes about this. Toward the end of page 14 he says this is invalid since the atmosphere radiates in 3-D, not just up and down. In fact, the quantity σT4 refers not only to the total power output of an object (the rate of energy emission), but it also refers to isotropic (equally intense in all directions) radiation. The result σT4 is obtained if one assumes that a plane radiates uniformly over a hemisphere (for example, the domed "half sphere" field of vision that a human can see when you stand outside, with the base of that half-sphere being the surface you sre standing on; the other hemisphere is invisible (see this image).
So far, it is simple textbook stuff with not much promise.
Geometry of the Global Energy Budget
Postma then goes on to describe fictitious “boundary conditions.” In particular, he seems to have serious objections to the averaging of the solar radiative flux over the Earth. In essence, he would prefer we had one sun delivering 1370 W/m2 of energy to the planet, with a day side and a night side, noon and twilight, etc. instead of the simple model where we average 1370/4=342.5 W/m2 over the planet (so that the whole Earth is receiving the appropriate "average" solar radiation). The number becomes ~240 W/m2 when you account for the planetary albedo (or reflectivity).
The factor of 4 is the ratio of the surface area to the cross section of the planet, and is the shadow cast by a spherical Earth. It is therefore a geometrical re-distribution factor; it remains “4” if all the starlight is distributed evenly over the sphere; it is “2” if the light is uniformly distributed over the starlit hemisphere alone; with no re-distribution, the denominator would be 1/cosine(zenith angle) for the local solar flux.
In simple textbook models, we like to prefer explanations that get a point across, and then build in complexity from there (see Smith 2008 for descriptions on a rotating Earth). Of course, students who use this model are probably educated to the point where they know that day and night exist, and certainly GCMs have a diurnal cycle. The radiative calculations are done explicitly by accounting for the temperature distribution and absorber amount that is encountered at each grid box. Postma is simply tackling a non-issue, just as how people criticize the term “greenhouse effect” for not working like a glass greenhouse. Postma objects to teaching this simple model because it is not real. All that is done, however, is to use a brilliant and sophisticated technique, taught only to the geniuses among us, called averaging! And of course, simple models are used in any classroom...it is how we learn.
But, in actuality, the globally averaged solar re-distribution approximation is not bad when we use it to describe the temperature for planets like Earth or Venus. These planets have an atmosphere or ocean that transport heat effectively, especially Venus with virtually no day-to-night or pole-to-equator temperature gradient. The atmosphere and/or ocean help smooth the diurnal temperature difference very well. Therefore, when coming up with a temperature estimate, it is a great first approximation. If you want the local equilibrium temperature for an airless body like Mercury or the Moon (that does not transport heat), then you want to use the no-redistribution or hemisphere only solar factor. This is well-known (see e.g., Selsis et al 2007). On Mercury, there is no heat distribution and very little thermal inertia; before the sunrise the temperature on the surface is somewhere near 100 K (-173 °C) and by noon the temperature on the surface of Mercury rises to about 700 K (427 °C). This may also be relevant for tide-locked planets (very slow rotation since one side is always facing the host star, the other in perpetual darkness). Earth does not experience any such changes of the sort. On Venus, the variability is even less, and most of the planet is at around 735 K.
Summary so far...
To summarize so far, Joseph E. Postma did not like a simple model of Earth’s radiative balance where we approximate the Earth as a sphere with uniform solar absorption. Of course, this is never done in climate modeling or in more detailed analyses appropriate for scholarly literature, so it is more an exercise in complaining about undergraduate education than an attempt to correct what he calls a “paradigm” in climatology. Nonetheless, the 0-D energy balance model is a useful approximation on Earth when coming up with an average emission temperature (~255 K), since air circulations and oceans tend to even out the diurnal temperature gradient on Earth, in addition to the thermal inertia provided by the system.
Venus is More Optically Thick Than a One Layer Model Can Give You
Postma starts by using Venus as a template for where the greenhouse model he is using breaks down. And indeed, he is right. His argument is that f (the emissivity) cannot possibly be greater than 1 (which is correct), and yet it must be in order to produce the Venus surface temperature in his Equation 29) Based on this, he then states that the standard greenhouse model does not work in general. The problem is that his Equation 29 assumes a one-layer atmosphere, which is an absurd assumption when you approach the extremely high optical thickness of Venus. Venus has a 90 bar atmosphere that has well over 90% carbon dioxide, some water vapor, and a greenhouse effect generated by suluric acid droplets and SO2. The radiative transfer on Venus works much differently than on Earth, owing in part to intense collisional broadening of CO2 molecules. A photon has an extremely difficult time escaping Venus, unable to do so until it reaches the very outer parts of its atmosphere.
Using the layer model, you would need many atmospheric layers to produce something close to Venus; with enough layers you would find that you could produce the surface temperature of Venus without violating conservation of energy. With just one perfect absorbing atmospheric layer, the surface temperature cannot exceed 21/4 times the emission temperature (Te=~230 K on Venus). But with two perfectly absorbing atmospheric layers, it can rise to 31/4Te. With three layers, the maximum temperature is 41/4Te, and so on. The reason the surface temperature is capped in this way is because the atmosphere itself must be emitting radiation and heats up when it absorbs photons from the surface, which in turn increases emission. If the atmospheric layer were instead a good infrared reflector (i.e., it has a high thermal albedo), then you could delay heat loss to space that way and increase the surface temperature well beyond this value. This could happen with CO2 clouds instead of H2O clouds, the latter are much more effective IR absorbers than IR scatterers, whereas the former could raise the IR albedo.
In essence, Postma stretches a simplified model to areas that it was never designed to go to, and then declares that its failure to work means the whole paradigm of the greenhouse effect is wrong. The incompetence is overwhelming. Postma is not done though, and decides to dig in further. His next argument is amusing, but perhaps a bit strange to follow, so I will try to explain.
Lapse Rate Confusion
He claims that observations of the atmospheric lapse rate (the rate at which temperature declines with height) disallow the greenhouse effect. His reasoning is that the atmosphere is at a fixed height. When greenhouse gases warm the surface, and cool the upper atmosphere, that height still remains fixed, but obviously the temperature difference between the bottom and top of the atmosphere must increase. Postma then claims that this necessarily implies that the lapse rate must have a greater slope than the theoretical value that he derived of about -10 K per kilometer (which is about right for a dry air parcel ascending). That is, if the atmospheric height remains fixed, and the temperature difference between bottom and top is increased, then the rate at which air cools with height must increase. Since this is not observed, then we have a problem, right?
In actuality, the atmospheric height is a distraction. The adiabatic lapse rate does not extend beyond the point where convection breaks down, which is the tropopause. The whole point of the greenhouse effect is that increasing atmospheric greenhouse gases does increase the “average” height at which emission to space takes place (and the tropopause increases in height too), so one IS allowed to extrapolate further down the adiabat to reach a higher surface temperature. On Venus, the optical thickness forces the tropopause to some 60 km altitude. Additionally, it is worth pointing out that greenhouse gases warm the upper troposphere, not cool it, but they do cool the stratosphere.
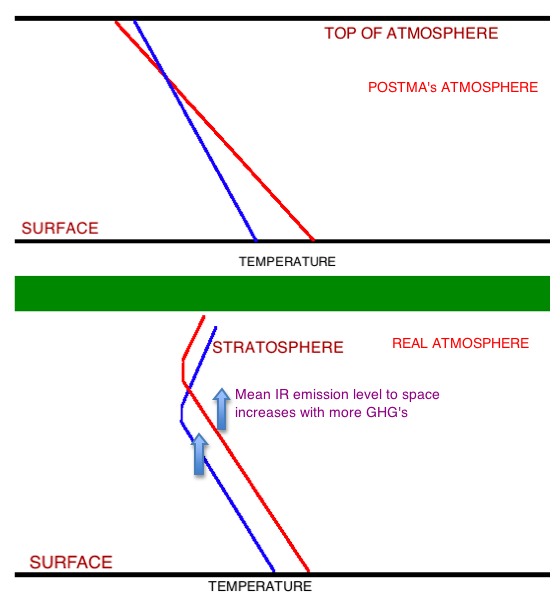
Figure 1: Qualitative schematic of the old (blue) and new (e.g., after CO2 increase) temperature with height in a dry atmosphere. Moisture tends to enhance the tropical upper atmosphere warming relative to surface. Temperature increases to the right.
TOA vs. Surface
Perhaps just as crucial to all of this, Postma cannot get around the surface energy budget fallacy, which says that increased CO2 causes surface warming by just increasing the downward infrared flux to the surface. This problem is described in standard treatments of the greenhouse effect, which he does not seem to know exist, such as in Ray Pierrehumbert’s recent textbook. The primacy of the top of the atmosphere budget, rather than the surface energy budget, has been known at least since the work of Manabe in the 1960s (see also Miller 2012)
In reality, the top of the atmosphere budget controls the surface temperature even more than the surface forcing, because the atmosphere itself is adjusting its outgoing radiation to space (and much of the radiation to space is originating in the upper atmosphere, owing to its IR opacity). Where the atmosphere is well-stirred by convection, the adjustment in temperature at this layer is communicated to the surface. I described this in more detail here.
Postma runs into this mistake again when he claims that the low water vapor in hot deserts is a problem for greenhouse theory, but this is largely due to the lack of evaporation cooling, which is just one component of the surface energy budget, and nearly absent in a desert. This is one scenario where a detailed consideration of the surface budget is critical, as well as in other weakly coupled regimes.
The way CO2-induced warming really works in a well mixed atmosphere is by reducing the rate of infrared radiation loss to space. Virtually all of the surface fluxes, not just the radiative ones, should change in a warming climate, and act to keep the surface and overlying air temperature relatively similar. The back-radiation will indeed increase in part because of more CO2 and water vapor, but also simply because the atmosphere is now at a higher temperature. But if the lower atmosphere was already filled with water vapor or clouds to the point where it emitted like a blackbody (at its temperature), increasing CO2 would not directly increase downward emission before temperature adjustment, but would nonetheless warm the planet by throwing the TOA energy budget out of whack.
Conclusions
In summary, Joseph Postma published an article criticizing a very simple model that nonetheless produces useful results. He made several very simple errors along the way, none of which are very technical in nature. More sophisticated models are obviously designed to handle the uneven distribution of solar heating (which is why we have weather!); nonetheless, the educational tools are useful for their purpose, and in no way does Postma undermine the existence or necessity of the greenhouse effect. Without a greenhouse effect, multiple studies have shown that the Earth collapses into a frozen iceball (Pierrehumbert et al., 2007; Voigt and Marotzke 2010, Lacis et al 2010) and indeed, after an ice-albedo feedback, plummets below the modern effective temperature of 255 K. This work makes extraordinary claims and yet no effort was made to put it in a real climate science journal, since it was never intended to educate climate scientists or improve the field; it is a sham, intended only to confuse casual readers and provide a citation on blogs. The author should be ashamed.
Note: broken link to the original paper by Postma, in the second line of the text, fixed on January 17, 2026. Thanks to an observant viewer.
Last updated on 1 January 2015 by . View Archives































 Arguments
Arguments




























[DB] Your two moderated comments were merely repetitions of unsupported assertions you made earlier, here. Supporting the earlier assertion with links to peer-reviewed studies appearing in reputable journals would be an example of adding to this discussion. Merely repeating yourself, such as you did, detracts from the discussion and begs intervention by the moderation staff.
[DB] "From the NASA data, it looks like you are wrong at every step."
This is insufficient in a science-based forum and amounts to you being argumentative for form's sake. If you disagree, it is incumbent upon you to do the maths (show your work) or to provide supportive links with an appropriate measure of explanatory context as to what you understand the link to show and why it is pertinent to the discussion.