From the eMail Bag: the Beer-Lambert Law and CO2 Concentrations
Posted on 20 December 2021 by Bob Loblaw
We occasionally receive excellent questions and/or comments by email or via our contact form and have then usually corresponded with the emailer directly. But, some of the questions and answers deserve a broader audience, so we decided to highlight some of them in a new series of blog posts.
Recently, an email asked about CO2 and the absorption of infrared (IR) radiation (specifically mentioning the 15 μm wavelength). The email mentioned the Beer-Lambert Law, and went on to ask how a gas can have any effect at low concentrations (400 ppm, or 0.04% of the atmosphere).
This post will attempt to explain what the Beer-Lambert Law tells us about the absorption of radiation, and explain why 400 ppm of CO2 can still be an important factor. We’ll look at some of the differences between visible light and IR radiation, and perform a small experiment to show that how we measure “concentration” is important.

Figure 1. Lighting at sunset - atmospheric radiation transfer at work
Background
It is well known that different wavelengths of light interact differently with the atmosphere. An example we are all familiar with is the difference in lighting between mid-day and twilight. At mid-day, we see a normal (to our human eyes) distribution of the spectrum of light - a balance between the various colours of the rainbow we all learn in school: red, orange, yellow, green blue, indigo, and violet. As the sun sets, the long path the light takes through the atmosphere means we see a colour distribution with much more red in it. To the delight of photographers worldwide, there is a special quality to the lighting that makes landscapes change their appearance (figure 1).
There is also a very strong difference between the way solar radiation (from the sun) and terrestrial radiation (emitted within the earth-atmosphere system) interact with the atmosphere. Solar radiation comes in the UV, visible and near-infrared portions of the spectrum, and terrestrial radiation is in the infrared. Figure 2 shows the theoretical Planck curves for radiation emitted from two sources – one at a temperature of 5800K (similar to the sun), and the other at 255K (typical of the earth-atmosphere system).
Each follows a curve, with a peak somewhere in the middle. Solar radiation is mostly in the visible range, between 0.4 and 0.7 μm, and nearly all the energy falls between about 0.2 and 2 μm. Terrestrial radiation peaks at just over 10 μm, and nearly all the energy falls in the range between 4 and 40 μm. We can see that the two ranges do not overlap in the portions of the spectrum where most radiation is emitted from each source.
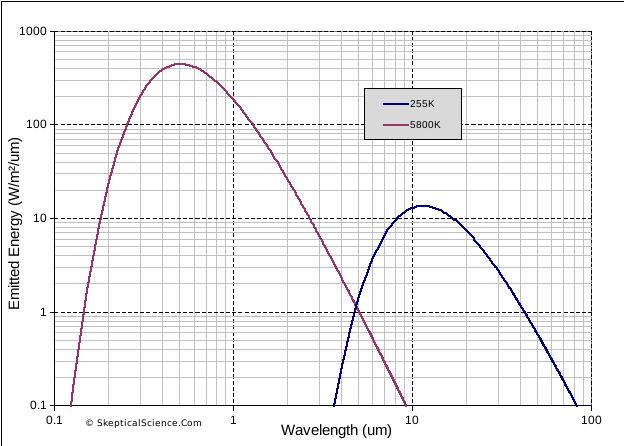
Figure 2. Theoretical emission curves (Planck curves) for sources at 5800K (solar) and 255K (terrestrial)
This difference between solar and terrestrial radiation wavelengths is a key aspect of the greenhouse effect. The atmosphere is mostly transparent to solar radiation wavelengths, so energy from the sun easily reaches (and heats) the surface. In contrast, the atmosphere readily absorbs IR radiation, so energy emitted from the surface is not easily transmitted through the atmosphere back to space. The effect of the atmosphere – reducing the efficiency of energy loss from the surface to space – is the essential characteristic of “the greenhouse effect”. Instead of surface temperatures being in the region of 255K (-18°C), our planet is a habitable average of about 288K (15°C). And if we add gases that absorb additional IR radiation, such as CO2, we will increase this heating effect (global warming).
The Beer-Lambert Law and the concentration of absorbing gases
So, what was it that our email writer was asking about? Well, the question had to do with the low levels of CO2, and how a gas that exists in such small quantities in the atmosphere (400 ppm = 0.04%) could possible have an influence on climate. The writer was aware of several important factors:
- The Beer-Lambert Law tells us how much radiation is absorbed as radiation passes through a volume of material,
- The absorption is dependent on the concentration of the absorbing gas (CO2, in this case),
- This relationship differs for different wavelengths, and
- That different gases have different absorption characteristics.
...but the writer speculated that it would take 100% CO2 to absorb all the 15 μm IR radiation, and that 0.04% CO2 would only absorb 0.04%. How could such a small concentration have any effect? The email writer has misunderstood some aspects of radiation absorption, and come to an incorrect conclusion.
To explain this, we need to look a little more closely at just what the Beer-Lambert Law tells us, and how this applies to the atmosphere. Wikipedia has a good article on the Beer-Lambert Law, but it doesn’t really tell us how to apply this to CO2 and climate.
The Wikipedia page’s first equation (yes, we need equations...) is:
A = εLc
where
- A is the absorbance (fraction of radiation absorbed)
- ε is the “molar attenuation coefficient”
- L is the optical path length (how long is the path through the material)
- c is the concentration of the material that is doing the attenuating.
(“Attenuation” is a fancy term for the combination of absorbing and scattering. More on that later.)
So, we can see here how the email writer is thinking in terms of “concentration”. The catch is, thinking of CO2 in terms of parts per million – comparing it to all the other gases in the atmosphere – is not the correct “concentration” that is needed. The equation multiplies three terms. Let’s look at the one at a time.
The first is the “attenuation coefficient”, ε. This is molar attenuation – where molar is a count of the number of molecules. (Since there are so many molecules involved, chemist usually talk in terms of moles, which is the number given by the Avogadro constant.) When expressing CO2 in “ppm”, we are talking about how much CO2 there is as a proportion of how much total gases are present. So, if we have a volume of air that contains 400 molecules of CO2 and 1 million molecules of air, we have 400 ppm of of CO2. But if that same volume of air contains 4,000 molecules of CO2 and 10 million molecules of air, we still have 400 ppm of CO2 even though there are ten times as many molecules present. To radiation passing through that volume of air, these two cases are not the same. It is the number of molecules that matter.
Figure 3 shows this. Although both sides of the diagram have 40 red symbols per 1000 symbols (or, 40 parts per thousand), the left diagram is packed with 1000 symbols in total, and the right diagram has only 100. Clearly, the left diagram represents a case where more absorbing will occur. Also, we should remember that different gases that absorb differently at different wavelengths. This means that they act more or less independently. In figure 3, the effect of the red symbols – 40 on the left side, or 4 on the right side – is not much affected by how many blue symbols there are. In fact, if you just took all the blue symbols out, we’d still have the same number of red symbols and they would have the about the same effect – even though the red symbols are now 100% of all the symbols. (There are additional details involved, but as a first approximation, this is the case.)
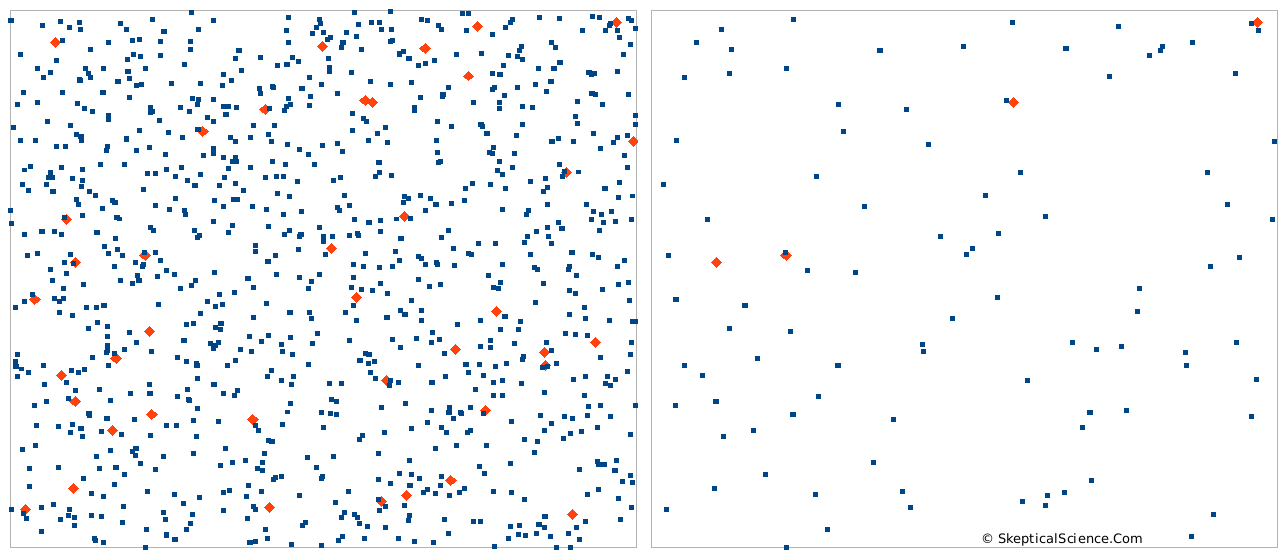
Figure 3. Two boxes, each with 40 parts per thousand (ppt) red symbols, but different absolute amounts.
So, to match the attenuation term, ε, the concentration that we need (the c term in our equation above) needs to be a count of the absolute number CO2 molecules in the volume of air – the molar concentration – not its ratio to the other gases.
If we apply the ideas from figure 3 to our atmosphere in a thought experiment, think of CO2 as the red symbols and N2 as the blue symbols. In the atmosphere, CO2 is 0.04%, and N2 is about 78%. N2 is transparent to IR radiation - it does essentially no absorbing. What would happen if we removed all the N2? CO2 would now be 0.18% of the atmosphere - but will it be absorbing almost 5x as much IR? No. There will be some minor changes related to the air pressure change, but the CO2 is present in the same number of molecules, and it will be doing basically the same absorbing. (Removing all the N2 would alter the overall greenhouse effect, because convetcton is important. Having 1/5 the mass in the atmosphere will affect convection - but that is another story for a different blog post.)
Back to our equation. The term in the middle, L, is the path length. We multiply the concentration by the path length. If concentration is in moles/m3, and we multiply by the length in metres, then Lc is in moles/m2. And then when we multiply by the attenuation coefficient (units are “per mole”), then we end up with units of “per m2”. Since we always talk of radiation in units of “per m2” (e.g. Watts/m2), this is exactly what we need - A = εLc will tell us the fraction of our radiation that is absorbed.
So, we can see here that we need concentration in the correct units, and we also need to think about how far through the atmosphere the radiation needs to travel – a longer path (at the same concentration per m3) means more absorption.
Application to the atmosphere
Now, let’s try to think how this all works in the atmosphere. Figure 4 shows this visually. In the top part of the diagram we see a cylinder that represents a small portion of the atmosphere. Radiation (photons) coming in from the upper left can do three things:
- Pass straight through, with no change in direction, emerging on the lower right. This is “transmission”. (Quantity A)
- Be scattered, through interactions with the mass inside the cylinder, so that the direction is changed. The radiation will now come out of the cylinder travelling in a different direction. (Quantity B)
- Be absorbed, through interactions with the mass inside the cylinder, so that the energy in the photons is transformed from radiation energy into thermal energy. The radiation “is no more” (although the energy is conserved as heat). (Quantity C)
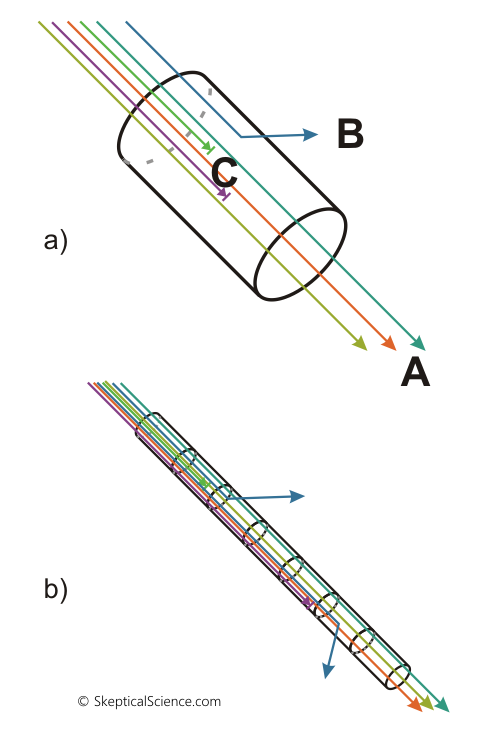
Figure 4 – Diagrammatic view of atmospheric transmission (Beer-Lambert law). Top: a single "unit" of air. A = transmitted, B = scattered, C = absorbed. Bottom: a chain of multiple units of air.
We haven’t said much about scattering yet. In the atmosphere, scattering can be caused two ways: Rayleigh scattering, or Mie scattering. Both depend on the size of the particles in relation to the wavelength of radiation. Rayleigh scattering is caused by the air molecules themselves (much smaller than the wavelengths of radiation), and is strongest in the UV and blue end of the visible spectrum, and weak at the red end. It is essentially non-existent in the IR range. Mie scattering is caused by small dust particles, etc., and radiation is only scattered in wavelengths similar to the particle size. Mie scattering also only affects visible light, because particles large enough to scatter IR radiation are too large to stay suspended in the atmosphere.
As a consequence, when discussing IR radiation we can ignore scattering and only need to think about absorption. Remember earlier when we mentioned “attenuation”? Well, when we see a reduction in radiation – the “transmitted” amount leaving the cylinder is less than the amount entering the cylinder in figure 4 – we can’t tell whether it was absorbed or scattered. So, we put “absorbed and/or scattered” into one group, and call it “attenuated”. For visible light, absorption and scattering both occur and we need to know how much of each is happening. For IR radiation, though, scattering is zero so any radiation that was “attenuated” was absorbed.
Let’s get back to figure 4. We can see in the top diagram how we have radiation being transmitted, absorbed, or scattered as it passes through a volume of air. In the bottom diagram, we have just chained together a series of cylinders. As radiation passes through each cylinder, it will react according to the Beer-Lambert Law, and we will see a continued reduction in transmitted radiation. We need to be careful how we calculate the result, though. It is not a case of simply adding them together – we actually need to multiply them:
If one cylinder absorbs 1% and transmits 99%, then it is a mistake to think that 100 cylinders end-to-end will absorb 100x1% = 100%. Why? Because the “1% per cylinder” is not 1% of the original radiation amount – it is 1% of the amount that was passed from the first cylinder to the second, and the second to the third, etc.
Instead, it is easier if we think of how much is transmitted. If 1% was absorbed, then 99% was transmitted.
- 100% enters the first cylinder, and 99% leaves (transmitted).
- The second cylinder receives 99% of the original 100%, and transmits 99% of 99%, not 99% of 100%. The amount passed on to cylinder 3 is 0.99*0.99 = 0.9801 (98.01%)
- Cylinder 3 receives 0.9801 units, and transmits 0.993, or 0.9703.
- When we get to cylinder 100, we are still transmitting 0.99100, or about 37% of the original amount.
What we have is not a linear reduction in transmission, but an exponential one. This leads us to another common way of expressing the Beer-Lambert Law (also seen on the Wikipedia page linked earlier):
I(z) = I(0)e-μz
where
- I(0) is the original radiation amount,
- μ is the attenuation coefficient (per unit distance),
- z is the distance (usually called the “optical path length”),and
- I(z) is the amount of radiation remaining after distance z.
Figure 5 shows this exponential function for 200 layers of transmission, using two transmission values (0.95 and 0.9 per layer). If we mistakenly calculate that each layer removes 0.05 or 0.1 of the original radiation (y = 1 at x = 0), then we would conclude that transmission would reach zero after 20 or 10 layers respectively. As we can see, the exponential nature means that fully 1/3 of the original radiation will pass through 10 or 20 layers in these two cases.
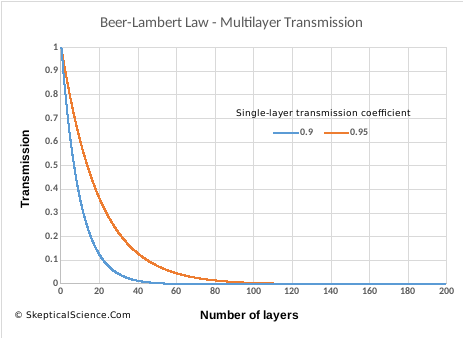
Figure 5. Transmission of radiation through multiple layers, from the Beer-Lambert Law, for two values of single-layer absorption (0.95, 0.9)
What is the practical significance of all this? Every child probably asks "why is the sky blue?" at some point. It is the difference in scattering of blue light (lots of scattering) versus red light (not much scattering) that gives us our nice blue skies. Without an atmosphere, we’d see a black sky with a bright white sun. The only reason we see light from other parts of the sky is because the atmosphere scatters the light, and more blue is scattered. And when the sun is low in the sky, it passes through a longer path in the atmosphere – as much as 40 times longer at sunset, compared to the sun positioned directly overhead. This removes even more blue light from the direct path, leaving a reddish sun. And that gives us the lovely lighting we see in figure 1.
For IR radiation? Well, there are two key things to consider:
- It does not matter than CO2 is only 0.04% of all the gases. What matters is the absolute amount in the atmosphere. And the amount currently in the atmosphere is enough to be very, very important.
- Even if we are at a wavelength where 200 layers containing CO2 will absorb essentially all the IR radiation, adding more CO2 will still change the amount that is absorbed after 2 or 5 or 10 layers (figure 5). You cannot assess the role of CO2 by only looking at the start and end. You also need to look in the middle. At current concentrations, adding CO2 to the atmosphere is still going to cause changes.
A simple experiment
All of this discussion started with the emailed question about CO2 ppm being so small, and not recognizing that it is the absolute amount of CO2 that is the important factor. When I first read the question, it made me think of a simple basement experiment I could try to illustrate how concentration in ppm was not important – the absolute quantity of an absorber is. I don’t know what you have in your basement, but I do not have any IR radiation measurement equipment. I do have methods of detecting visible light, though (a digital camera), and fortunately visible light and IR radiation both follow the Beer-Lambert Law.
Figure 6 shows the results of my experiment. There are four photographs, each taken with the same exposure settings. Here is what I did:
- I set a newspaper on the floor, with a bright light to the side (coming from the top of the photographs).
- I placed two identical glass storage containers on blocks of wood, over the newspaper, so that you can see the newspaper below (mostly lit by the bright light – i.e., a light source behind the container).
- The first photograph shows the light transmission through the two empty glass containers.
- The second photograph shows the two containers with 250 mL of water added to each. You can see that adding water, which is transparent to visible light, has had no significant effect. You can see refraction effects at the edge of the container/water surface, but no real difference in the middle.)
- In the third photograph, things start to change. Each container now holds 125 mL of water that contains a few mL of dilute dye (a powder dissolved in water – it happens to be a walnut dye I use to stain wood). Note that the two containers both block light from the newspaper in about the same amount.
- The fourth photograph is the key one to examine: both containers still contain the same amount of dilute dye, but the one on the left has now had 500 mL of water added. So, the dye is even more dilute (expressed as g/mL), but this has not resulted in increased absorption of light. The newspaper is still just as visible through both containers. In the left container, our dye concentration per mL is 1/5 of what it was in photograph 3, but the path length is 5x longer (more water). These effects cancel out as far as the dye is concerned, and since the water itself is transparent we see little change. Both containers have the same A = εLc.

Figure 6. A simple experiment on light transmission through coloured water.
This experiment could be improved by using containers with straight sides, taller, and with better lighting control, but what I did took me about 15 minutes and is easily done at home. Instead of woodworker’s dye, you could use food colouring, liquid ink, or even a coloured soft drink to create the semi-transparent liquid.
I thought about trying to take a picture of the two containers from the side, so you could see the effects of diluting the dye when the path length does not change (homework assignment!), but the round shape of the containers and the difficulty of getting good lighting passing through the sides of the containers wasn't working out. Refraction in the glass became important, rather than transmission through the dye solution..
Conclusion
That’s it for our review of the Beer-Lambert Law: how it relates to the absorption of IR radiation by CO2, and how to correctly measure CO2 concentration for this purpose.
This article only touches on the complexity of radiation transfer in the atmosphere, though. The Beer-Lambert Law only looks at a one-dimensional source of radiation travelling in a single direction. Atmospheric radiation transfer is a three-dimensional problem. For visible light, we get multiple scattering, and surface and cloud reflection. For IR radiation, the earth and atmosphere are also doing the reverse of absorption – thermal energy is being transformed into photons, resulting in the emission of IR radiation in all directions. The amount of IR radiation that comes out of a volume of air is a combination of what came in and was transmitted, plus amounts emitted inside that volume of air that are added to the stream of photons.
Yes, these complexities are known, and yes, the complexities do not change the conclusion that CO2 is present in high enough concentrations to be important, and that increasing CO2 will continue to cause significant climate change over time.
Skeptical Science has pages debunking two myths related to the discussion here:
CO2 is a trace gas.
In the “trace gas” post, the discussion focuses on how trace amounts of different substances can still be dangerous. The essential part of that argument is that you need to do the science to determine whether small amounts of something are important. The post here points out that CO2 expressed in ppm is the wrong units to use. Someone could still argue that the right units (molar concentration) may still be “small”, but the next step to that argument has to be “do the math”. Climate scientists have “done the math”. CO2 is important.
The CO2 effect is saturated.
In the “CO2 is saturated” post, the discussion debunks the myth that CO2 already absorbs all the IR radiation it can, so adding more will have no effect. (Notice how this is the complete opposite of the “it’s a trace gas” myth.) The reasons why that myth is wrong are complicated, but figure 5 (above) gives a good starting point: even if absorption approaches 100% after many layers, increasing the absorption per layer will have an effect in the middle layers. At hugely-high concentrations, CO2 will eventually “saturate” in a meaningful way, but we are a long way off that level.































 Arguments
Arguments






























This is an excellent description of Beer’s Law. The distinction between concentration (ppm or molecules per million molecules) and molar density (molecules per cubic meter) is very good. However, the described application to the atmosphere has a few shortcomings that leave an incomplete description of the effect of saturation. The description does not account for re-emission, nor the multiple absorption lines for CO2 of different intensities. It also does not describe the role of temperature stratification in the atmosphere. The conclusion does allude to some of these issues.
Rather than as cylinders, the atmosphere is better described as layers of shells. One problem with the description lies in the third path for the fate of radiation in a cylinder (Quantity C): “3. Be absorbed, through interactions with the mass inside the cylinder, so that the energy in the photons is transformed from radiation energy into thermal energy. The radiation ‘is no more’ (although the energy is conserved as heat).” However, as energy absorbed by a molecule, it is re-emitted to maintain thermal equilibrium. Re-emitted energy occurs in all directions, not just in a straight line. Therefore, re-emitted energy is lost to the walls of the cylinder. Meanwhile, in the atmosphere, there are no walls and re-emitted energy is absorbed and re-emitted again elsewhere in the atmosphere. In this manner, there are multiple absorptions and re-emissions in a convoluted path with some net energy flowing upward and some downward.
The key concept behind saturation lies in the different absorptances for each IR wavelength. Saturation occurs when the absorptance equals 1.0. The major peak at 14.98 microns is saturated first, then smaller peaks become saturated as CO2 increases. I wish that I could insert a graphic, but I haven’t figured out how to do it yet. Absorption lines can be seen using bytran, which is an open-source interface under the MIT License for the HITRAN database (Pliutau, D. and K. Roslyakov, “Bytran -|- spectral calculations for portable devices using the HITRAN database,” Earth Science Informatics, 10 (3), pp. 395-404. Feb 2017.)
Beer’s Law as related to the atmosphere comes into play with determining the uppermost layer that limits the escape of radiant energy to space through the 13 to 17 micron window for CO2 absorption/emission of IR. This layer turns out to be the bottom of the stratosphere at an altitude of about 30 km, just above the tropopause. At this altitude and considering a path length of 1000 meters, which is a reasonable distance in the atmosphere, there are still sufficient CO2 molecules to form an emission layer for CO2. It is a little harder to see the difference in the absorption lines at 400 and 800 ppm under these conditions, but this explains the diminishing effect of saturation.
It is common to think of radiant energy leaving the surface and trying to explain what happens as it works its way through the atmosphere. However, it is instructive to focus on the radiant energy exiting the top of the atmosphere rather than the energy leaving the surface. The lower stratosphere is the uppermost CO2 layer with sufficient molecules for an emittance of 1.0. Since absorptance equals emittance, this is the maximum emittance for that wavelength. This layer of the atmosphere is cold, so the radiance, total emitted energy, from this layer is less than the radiance emitted from the warmer surface. As the uppermost emitting layer, it becomes the limiting layer for radiant energy loss to space.
There is a saturation effect, but it is better illustrated using an atmospheric radiation model than using Beer’s Law with a number of cylinders. Using a simplified model, it can be illustrated that increased radiant IR energy flux lost to space from doubling CO2 from 200 ppm to 400 ppm is the same as doubling CO2 from 400 ppm to 800 ppm. This forms a logarithmic curve. The warming effect due to CO2 is saturating, but it is not saturated.
[BL] Regular commenters here cannot directly embed images from their local computers within the code/comments that are stored on the web site's servers. Images have to be stored on some other publicly-accessible server, and then you can link to them.
You have two options:
Under option 2, the image will no longer be displayed here if the original source deletes or renames it. The SkS web page does not cache the image.
Charlie Brown:
Yes, your discussion touches on some of “the complexity of radiation transfer in the atmosphere” that I dismissed in a single paragraph at the end of the blog post. The blog post was only intended as a counter to the “CO2 exists in small concentrations” misinterpretation of the Beer-Lambert law, and leaves a whole host of other fundamental principles in atmospheric radiation transfer to the imagination of the reader.
You refer to several issues that deserve more discussion – issues that take entire university courses or textbooks to cover. You mention at least four specifics I’d like to elaborate on:
With regard to re-emission, the amount of IR radiation leaving the cylinder is the sum of what was transmitted through the cylinder plus the amount that was emitted within the cylinder (and manages to leave before being re-absorbed within the cylinder). With regard to the emitted IR:
You mention IR lost through the side walls of the cylinder. There is also IR gained through the side walls, coming from adjacent cylinders that are behaving the same way as the one in figure 4. If the adjacent cylinders are identical, then each cylinder will be gaining and losing identical IR radiation amounts through the sides, so the net effect is zero.
Can we say the same things about the IR transfers between cylinders in the vertical stack of cylinders (figure 4b)? No, and there is a very important reason why. The net effect between adjacent cylinders (side by side, or top over bottom) depends on the temperature within each. If the temperatures are equal, the net IR transfer effect will be zero – but if they are not equal, there will be a net transfer from the warmer one to the cooler one. In the horizontal direction, temperature gradients are very small, so it is reasonable to ignore that direction. Vertically ,however, we see strong temperature gradients – the environmental lapse rate averages 6.5 C°/km. So, the top cylinder tends to be colder than the bottom cylinder, and the net IR transfer is upward.
So, we get to think in terms of up/down fluxes of IR radiation, and need to consider the thermal stratification of the atmosphere, as you mention. The up/down aspect has a formal label: the two-stream approximation. The extension of the use of the Beer-Lambert Law to include the emissions of IR radiation and the net IR flux along a temperature gradient also has formal solutions, one of which is called Schwarzschild’s equation.
Of course, the vertical temperature structure of the atmosphere is not purely due to radiation, so we can’t model it purely using radiation theory. Weather and climate models need to include convection, etc. - anything that transfers energy.
We also can’t leave the 3-d atmosphere discussion without mentioning clouds. Although gases in the atmosphere have absorption/emission characteristics that are highly dependent on wavelength, clouds (either as liquid or solid/ice) are essentially black bodies. In the same way that the two-stream approximation treats radiation transfer as either up or down, we can begin to cover cloud effects by dividing the atmosphere into a clear sky portion and a cloudy portion. Clouds have layers, too, and three-dimensional characteristics of clouds become quite complex, but the clear/cloudy categorization is place to start.
Lastly, you discuss saturation. I tend to dislike the use of that term, because it seems to mean so many different things to different people. One of the issues not mentioned in the blog post is pressure broadening, where overall increases in atmospheric pressure reduce the absorbance coefficient of the greenhouse gases such as CO2. This leads to a “law of diminishing returns” as CO2 concentrations increase, but we are far from running out of space on that one.
You use “saturation” in the context of IR radiation leaving the surface and escaping to space – and point out that nearly all the IR escaping to space is lost from the upper atmosphere. This is correct, and one way of looking at this is to ask “how many times will IR emitted from the surface be absorbed and re-emitted before the energy reaches the upper atmosphere and can finally be lost to space?” Even now, the probability that surface-emitted IR escapes directly to space is very small – but if adding CO2 increases the number of absorb/re-emit cycles from two to four, to eight to sixteen, etc., there is a reduction in the efficiency of transfer of energy from the surface to space.
For each absorb/emit cycle, only half gets emitted upwards. The half that emits downwards must go through at least one more absorb/emit cycle to get moving upwards again – and it only has a 50% chance that the next absorb/emit cycle will get it going in that direction. If it emits downward again, then it needs another absorb/emit cycle – with only a 50% chance again that it will emit in the upward direction. Adding more and more CO2 will always increase the number of absorb/emit cycles involved, but there is a law of diminishing returns here, too, which leads to the closing paragraph of yours where doubling CO2 from 200 to 400, or 400 to 800 ppm will have the same warming effect. Remember that convection is involved in that warming response, too – as radiation transfer becomes less efficient, convection takes a more dominant role (and it is already important).
Bob, thank you for your prompt and detailed reply to my reply. I enjoy technical discussions on the details of the warming mechanism and find few willing to engage at this level. I also think that it is important to have a solid understanding of the concepts to counter claims made by deniers, which often are based on a kernel of truth with explanations that are badly distorted. The concepts are complex, but they can be simplified. One does not have to be a climate scientist expert, university professor, or math whiz to work through them. I am a retired chemical engineer who took some radiation heat transfer courses in college, and have developed most of my thinking about global warming over the last 2 years.
Regarding measurements of attenuation by CO2 in a cylinder, the photons that are absorbed by a CO2 molecule are re-emitted, most likely toward the wall where they will be absorbed and converted to thermal energy. The energy will not be re-emitted from the walls at the same wavelength as emitted by CO2. It is unlikely that they will travel in a straight line and be measured at the end of the cylinder. Beer’s Law of attenuation describes the fate of the photons that are emitted from a source until they strike a target, not what happens with re-emitted photons. This is why I like to describe the atmosphere as layers of shells that have no sidewalls. Multiple stacked cylinders with adjacent, transparent walls is the same thing.
Regarding re-emission, it took me a long time to think through the problem of attenuation of surface IR through layers of the atmosphere and trying to figure out how many layers it would take as half of absorbed/emitted energy does up and half goes down. Finally, I realized that it is unnecessary to start at the surface and think about re-emission, convection, conduction, evaporation and condensation. Global warming is the result of the overall system energy balance, which is simply:
Solar energy in = IR emitted to space from the uppermost emitting layer for each IR wavelength + Accumulation
In the 13-17 micron range, Beer’s Law explains that the uppermost emitting layer is the lower stratosphere for many wavelength peaks emitted by 400 ppm CO2. The uppermost emitting layer for other GHG depends on their molecular density. For water vapor, the uppermost emitting layer is the troposphere, where the temperature is warmer than the bottom of the stratosphere. At wavelengths transparent to GHG, the emitting surface is the earth’s surface. It doesn’t matter how many layers, or cylinders, of 1% or of 90% attenuation are stacked in the lower atmosphere. Again, radiant energy lost to space depends only on the uppermost emitting layer. Where there are CO2 molecules, photons will be emitted at an intensity related to the temperature. There does not need to be conservation of photons from those emitted from the surface. Any imbalance in the photon count will be manifested as thermal energy changes, including by conduction to adjacent non-GHG molecules.
The link that you provided to Schwarzschild’s equation provides excellent descriptions of the essential role of the lapse rate, as well as attenuation. If I am not expressing my thoughts clearly enough, I recommend reading the sections on “Origins of the greenhouse effect,” “Saturation,” and “Applications to climate science” in that linked Wikipedia article.
The figure that I wanted to show is very similar to Figure 1 from this document from SpectralCalc.com Calculating Gas Spectra.
The diminishing effect of increasing CO2 is due to the increasing absorptance (decreasing transmittance since a = 1 – t) of the absorption lines on the “wings” or “shoulders” of the spectrum between 14 to 16 microns (wavenumbers 625 to 714 cm-1). The major peak at 15 microns (668 cm-100) reaches an absorptance of 1.0 with increasing path length or increasing CO2 first, then the other peaks follow with further increases.
The graph can be replicated or plotted for other concentrations and conditions using the Gas Cell Simulator in the free demo version of SpectralCalc.com. The gas cell is the same as the cylinder in the previous discussions, but as used for the graph, it illustrates the strength of each absorption line. The transmittance is different for each wavelength. The free version is limited to wave numbers. This is another way to interface with the HITRAN line-by-line database.
An interesting article, but I have to disagree with the main point: The Beer-Lambert law is not applicable here.
The Beer-Lambert law applies to attenuation or absorption. But in the case of the interaction of IR radiation with CO2 we also have re-emission. That, after all, is how we get downwelling radiation and hence the Greenhouse Effect.
The principle of detailed balance dictates that in thermal equilibrium the re-emission must reverse the absorption process, so the combined process looks like scattering. And the maths of scattering is different to that of attenuation.
The big difference is that the transmission coefficient is no longer exponentially dependent on layer thickness, x, as e-kx, but instead has a reciprocal dependence of the form 1/(1+ax). For an explanation see here.
The net result is that the transmission tends to zero much more slowly as x increases than it would with just attenuation. In practical terms it is a small point because the transmission is still less than 2%. But what it does mean is that the temperature rise with increasing CO2 is greater (but still small).
CD:
You are making some pretty strong assertions for someone that has clearly not read the entire post and comments in detail.
As is stated at the end of the original post, "For IR radiation, the earth and atmosphere are also doing the reverse of absorption – thermal energy is being transformed into photons, resulting in the emission of IR radiation in all directions." This is also discussed in more detail in the comments by charlie_brown and myself. You are not introducing any concept that has not already been mentioned. The post acknowledges that there are additional concepts that are needed for the full picture.
It may be a matter of semantics, but you are wrong in saying that the Beer-Lambert Law "is not applicable here". It is only part of the story, but is is clearly applicable to the absorption part of the story.
Where you go wrong is in claiming that the process of re-emission "looks like scattering". It most certainly does not. Scattering results in changing the direction of travel of radiation - but the radiation is still the same wavelength as the incident radiation, and each photon carries the same energy it had before it was scattered. You cannot create new radiation travelling in a new direction at a new wavelength through scattering, and scattering will not create new radiative energy. Emission does create new radiation.
For absorption/re-emission, the emitted IR radiation will not necessarily be at the same wavelength as any radiation what was absorbed. The absorbed radiation energy is not immediately emitted as new IR radiation - it virtually always gets lost by the GHG molecule to other molecules (including non-GHG ones). There is a good description of this over at Eli's. The energy that appears as emitted IR radiation does not need to come from the absorption of radiation - it almost always comes from collisions with other molecules that can get their energy from anywhere.
As a result, any emitted IR radiation is dependent on two factors:
As mentioned in comment #2, Schwarzschild’s equation covers the case where an atmosphere is both absorbing and re-emitting, and the net change in IR radiation with height is dependent on the temperature gradient.
One thing you have correct: IR radiation is equal in all directions, and in this sense it resembles scattered light (which occurs in all directions, but is not exacly equal in all directions), but that is the only similarity.
A key aspect of the dependence of net IR radiation on the temperature gradient is that upward IR fluxes normally decrease with increasing height, while downward IR fluxes normally increase as you go lower in the atmosphere. If we applied your concept of "transmission" to the downward flux, we would have transmissivity >1, This makes no sense.
"Transmission" is not a useful concept when the air can create new IR radiation and add it to the stream. It is a concept that only applies to IR radiation that originates elsewhere and is passing through the air. And that is exacly what the Beer-Lambert Law describes.
I have briefly looked at the URL you provided. It suffers from the same basic errors: confusing re-emission with scattering, and treating the addition of emitted IR to the upward stream as if it is a "transmission" question. It is not.
Proper radiation transfer theory and the effects in the atmosphere take into account all energy fluxes, and properly account for the process of absorbing IR radiation, transforming it into thermal energy contained in all gases, possibly moving it through convection, and then re-emitting that energy as IR radiation (by all GH gases).
charlie_brown:
The image from figure 1 of the SpectralCalc document you link to would be this one:
This diagram clearly shows the high level of variation with wavelength. Radiation transfer codes vary in their spectral resolution. You mention HITRAN. There is also a web site here that lets you work with an older lower-resolution model: MODTRAN. You can select different temperature profiles, change gas concentrations, cloud cover, etc., and choose looking up or down at selected altitudes.
All of the equations discussed - Beer-Lambert Law, Schwarzschild equation, etc. - are most properly applied to spectral radiation where properties such as absorption coefficients are highly variable with wavelength. For solids and liquids, some ranges of wavelengths can be treated as having proprties that are fairly constant. That is a Bad Idea (tm) for gases though.
The "cylinders" in the blog post diagrams and discussion are theoretical ones: the walls are perfectly transparent and do nothing to impede any sort of energy transfer. In the real world, the equations are differential ones. Keeping things simple usualy means not doing Calculus, though.
Introductory meteorology courses love talking about "parcels of air" (e.g. for explaining atmospheric instability), but of course the atmosphere is made up of continuous flows of air, not small balloons of air. Likewise, radiation does not work with distinct cylinders of air, but with air as a continuous medium. Your "shells" are an infinite number of identical stacks of columns, side by side.
@6 Bob Loblaw
Ok, perhaps saying the Beer-Lambert Law was not applicable was a bit strong. But my point is that relying on it, and it alone, gives the wrong answer for the amount of radiation that is transmitted through the gas. More importantly it underestimates the transmission for large thicknesses of gas as my original comment (@5) states, and so underestimates the impact of any large increases in the CO2 concentration.
As for the idea that my "concept of transmission" leads to a transmissivity > 1, the equations 88.8 and 88.14 set out here clear demonstrate otherwise. It is also true from the equations set out in the link that the reflected radiation flux Id is always less than that upward IR flux Iu at all altitudes x.
Finally, before claiming that energy transfers from CO2 to non-GHG molecules (and back again) invalidate my analysis, I suggest you look again at the principle of detailed balance. In thermal equilibrium, what goes in must come out, otherwise you start to violate the 1st & 2nd laws of thermodynamics. Yes there are complicating factors such as convection and direct heating of the atmosphere from the Sun, but these are secondary issues.
I am aware that the atmosphere is a complicated body, but that does not mean it cannot be largely understood by considering idealized models in the first instance. That is how modellers approach the problem. The Beer-Lambert Law is one such idealized model.
CD @ #8 and prior :
Best if you avoid the blogsite you have linked to [ClimateScienceInvestigations blogspot by "Climate Detective"].
It is one of those sad blogsites where much is correct, but much is wrong.
Rather like the famous "Curate's Egg" ~ where parts of it are quite good, but parts of the egg are rotten.
The "good" parts can never compensate for the bad parts.
CD @ 8:
Well, on your own web site, equation 88.1 is stated to describe the situation when the atmosphere is in "thermal equilibrium". (I assume you mean that temperature is not changing with time, rather than the atmosphere is isothermal.) You also claim that this implies an equality between absorbed radiation and emitted radiation. You are wrong, in more ways than one.
Look at the graphs provided by the MODTRAN web site I mentioned previously. It defaults to "looking down" - i.e., upwelling IR. Choose altitudes of 2, 5, 10 km etc and see how the IR flux decreases as height increases.
Now, repeat with the "looking up" option (downwelling IR). See how the fluxes increase as altitude decreases - i.e., as the IR radiation continues in the downward direction, more and more IR radiation is added to the stream. You cannot interpret this as "scattering with transmission <1". If your theory of the mathematics is correct, this increasing IR radiation requires a transmission coefficient that exceeds 1.
Your mathematics are not correct. They assume things that are not true (absorption = emission, non-radiative energy fluxes are not important).
If you follow the link to Schwarzschild’s equation, you will see that it has independent terms for absoprtion and emission - terms that cover the Beer-Lambert absorption and the Planck emission. This is the correct way to do it.
You started your comments here with the statement that the Beer-Lambert Law does not apply. The argument that you have presented appears to implicitly suggest that Planck's Law also does not apply. You have invented your own theory of radiation transfer, and it has some serious problems.
Eclectic:
I think that CD = Climate Detective, so you may have a tough ride ahead trying to convince CD that something on his web site is not worth linking to.
Bob @ #7
Thank you for providing the graph for HITRAN data. The point that I wanted to make is that increasing CO2 increases the individual high resolution absorption lines in the wings. That is why the effect of CO2 is not “saturated,” but is diminishing with increasing CO2. Moderate transmission programs use algorithms to simplify the detailed line-by-line calculations into an absorption band. Essentially, it is an approach to average the lines within an absorption band, which makes the calculations easier. With this approach, increasing CO2 increases the width of the band, effectively by increasing the inclusion of small lines at the end of the wings.
I have used the version of MODTRAN hosted by the University of Chicago quite a bit, and I find it to be an excellent tool for understanding atmospheric radiation. It is similar to the free demo version from Spectral Sciences, Inc Fortunately, it makes all of the calculations, including Beer’s Law, molar density, temperature, pressure, etc., for you. There is no need to do a lot of math on your own. It is easy to run several cases and plot the Upward IR Heat Flux as a function of increasing CO2. The upward IR heat flux is the energy lost to space. It becomes apparent that the diminishing effect is logarithmic. Because it is an atmospheric radiation model and not an energy balance model, it is a little bit trickier to resolve the overall heat balance to determine the effect on surface temperature, but it can be done. The surface temperature is an input with a default value of 299.7 K for a tropical atmospheric profile and 288.2K for the 1976 U.S Std atmosphere. One can adjust the surface temperature manually, then use trial-and-error to find a surface temperature that causes the overall global energy balance to be closed. This means the upward IR heat flux needs to be constant, since the only other factor in the balance is solar energy in. The logarithmic diminishing effect of increasing CO2 is the same.
CD,
While Beer’s Law is valid, using it to track the fate of radiant energy by wavelength leaving the surface is problematic. In the lower atmosphere, the 14-16 micron band reaches 100% absorptance within only about 100 meters. With re-emission, half up and half down, it doesn’t take many kilometers before the absorption band is depleted. However, radiant energy emitted from CO2 depends only its presence and its temperature. It does not depend on the path or number of absorption/re-emission exchanges. The temperature profile for radiant emission in the troposphere is determined by the lapse rate. Conduction between molecules keeps CO2 at the same temperature as the atmosphere.
IR that makes its way back to the surface is not the way to determine the effect of a change in CO2 on surface temperature. The surface temperature results from the overall global energy balance. It is much easier to consider the radiant heat loss to space as it is the only output energy stream for the balance. In the range for CO2, the principles of Beer’s Law determine that the uppermost emitting layer for that range is in the tropopause and lower stratosphere, which is cold at 217 K. For the US Standard atmosphere, the tropopause lies between 10-20 km. The available path length is very long. At an altitude of 20 km, the pressure is about 5% of 1 atmosphere, so 100% absorptance can be reached in about 2000 . Despite the low pressure, there are sufficient molecules in the path for CO2 to have a significant effect on radiant heat loss.
As CO2 in the cold tropopause increases, the absorption lines extend and the absorption band widens, reducing the heat loss to space. To return the energy balance to steady state, the reduced heat loss must be compensated by increased energy radiating through transparent wavelengths. This can only be accomplished by increasing the temperature of the source, which is the Earth’s surface. The effect on the IR spectrum of the Earth-atmosphere system as viewed from space will be a decrease of energy flux in the wavelength bands that are absorbed by GHG and an increase of flux through wavelengths that are transparent to IR. This effect is described in detail Brindley, H. E., and R. J. Bantges, “The Spectral Signature of Recent Climate Change,” Current Climate Change Reports, 2 (3), pp. 112–126 (Sept. 2016).
charlie_brown @ 12:
Your use of the phrase "saturation" (even though you put it in scare quotes) with respect to the broadening of the absorption wings, etc., is one of the few contexts where "saturation" makes sense.
Most of the "arguments" made that claim the CO2 effect is "saturated" (as I linked to in the original post) seem to look at the overall transmission after a long path length, and "saturated" does not make sense in that context.
The question of the degree of resolution of spectral radiation calculations is a valid one. To run a GCM at many points and many time steps, you can't do a full high-resolution radiative transfer model. (Well, you couldn't 40 years ago. Computer horsepower is greater now - I'm not sure what is included in current GCMs.) You can, however, use a lower resolution model and test it against the high-resolution models to make sure it is getting the important bits right. Of course, the high-resolution models are ultimately validated against measurements.
As a further comment on upper atmosphere IR transfer, two of the early key papers in this field were:
Manabe and Strickler, 1964
Manabe and Wetherald, 1967
A key finding of this work is stratospheric cooling in response to increased CO2, shown clearly in figure 16 from the second paper.
You will find many detailed explanations of this effect across the 'net, but one aspect of it is that adding CO2 also increases the emissivity, which means you get greater IR emission at the same temperature. In the stratosphere, where IR is easily lost to space, this increase in emissivity means that the earth-atmosphere system can emit the same IR to space at a cooler temperature. In the stratosphere, the Plancks' Law emission response to increased CO2 is stronger than the Beer-Lambert Law absorption response.
[BL] 2022-08-06 image link fixed
Bob @ 10, 14, 15
Good posts. Thanks for the references to Manabe. Both of these articles and also Modtran are referenced in the justification and scientific background for the Nobel Prize in Physics 2021.
Sorry for the re-post to CD. I am new to this site and fumbled the submit button.
[BL] I deleted the duplicate copy...
I encountered the Manabe and Strickler/Wetherald papers as a grad student in the 1980s, when they were still fairly new.
The Manabe and Wetherald paper is also part of The Warming Papers.
I often find that older papers cover more of the basics than you find in newer papers. Newer papers do not repeat the well-established science, and often tend to assume certain knowledge on the part of the informed reader. This is also true of the IPCC reports - for the basics, I often suggest reading the first one from 1990.
Thank you, Bob Loblaw @11
CD = Climate Detective . . . well now, who da thunk ;-)
But it is now more than 24 hours since the presumed bloggy author has posted here at SkS. Likely he has sailed away . . . or quite possibly sunk (considering how you delivered some heavy hits below his waterline).
To save SkS readers from wasting their time on the Climate Detective's blogsite, I will give a quick thumbnail sketch of the blog's contents. The author's blog contents range from: some technically correct stuff . . . to some definitely incorrect stuff . . . through to some quite bizarre stuff.
Much of the author's content has a mildly Wattsupian flavor . . . such as the cherrypicking of temperature charts for times and regions which are intended to demonstrate the wrongness of mainstream climate science & of all the national scientific bodies. That sort of thing ~ rather Wattsupian, but with a soft-pedal on the International Conspiracy Theories.
Then there was a slightly political take on the recent International Climate Conference in the UK ~ and the disastrous immorality of cutting out the consumption of petroleum oil. # "we [the rich West] will devastate the economies of many [Third World] oil producers." (Such callous disregard . . . cataclysmic impact . . . etcetera.) But # "alternative strategy . . . getting the producers to cut supply by 5% per year . . . result . . . global economic collapse."
~ An interesting demonstration of Motivated Reasoning. Binary thinking - only two future possibilities in that direction: Catastrophe A or Catastrophe B . Third or fourth possibilities are not conceivable. (Such is the effect of emotional bias on the intelligent mind - and there is no doubt that the author has an above-average I.Q. )
Elsewhere, the author raises the flag of Chaos, and becomes almost mystical: "[the AGW] that climate scientists think they are measuring is probably all just low frequency noise resulting from the random fluctuations of a chaotic non-linear system." And more: "this is because the fluctuations are actually the result of dynamic effects that played out long ago but which are only now becoming visible." (Not even the good Dr J. Curry rises to such elevation of the Butterfly Effect.)
And more (after plotting certain noisy graphs) ~ With a grand sweep of a mathematical wand, the author abolishes the multi-millennial swing from glaciation to deglaciation; abolishes Milanovitch cycles; abolishes solar variability . . . CO2 variations . . . volcanic aerosols . . . etcetera.
Apparently it is all a result of chaos mathematics and fractal geometry and self-similarity in nature. By this time, the author has disappeared down a fractal rabbit hole, into his own microcosmic concepts. He has failed to recognize that his ideas are unphysical.
[BL] Although I usually hesitate to step in as moderator when I am participating in a discussion, in this case I am also the author of the blog post and all this discussion of what someone may have on their own web site is really getting off topic.
Please restrict your comments on CD's views of climate expressed on his own web site to the items that CD links to in support of his statements here.
As for CD's response time - it's the holidays. Lighten up.
My apologies, BL ~ I should have allowed more response time than 24 hours (and perhaps moreso in a holiday period).
My concern was that the readers (other than myself) might be unaware of the relevant context of CD's thinking. Yes, we should focus on the precise point of argument put forward by any protagonist at all, however unphysical their background ideas.
The original emailer has sent in a follow-up to the Skeptical Science contact page, asking about black-body radiation and differences between emissions at 255K and 288K. A temperature of 255K is the commonly-cited radiative temperature at which the earth-atmosphere system emits IR radiation to space, while 288K is the commonly-cited global mean temperature for the earth's surface. The difference is a measure of the role of the atmosphere - the greenhouse effect - and this difference is predicted to continue to rise as atmospheric greenhouse gases continue to increase.
The blog post focuses on atmospheric absorption, not emission, but atmospheric absorption by CO2 is a key factor in the greenhouse effect. So, how might that temperature difference - 288K at the surface, 255K at high altitude - affect this process?
A few of the comments to the post touch on aspects of IR emission, and in figure 2 and comment #10 I mentioned Planck's Law, which governs radiation emission. Figure 2 was intended to show the difference between solar (5800K) and terrestrial (255K) sources of radiation, but does not touch on differences for the range of temperatures within the earth-atmosphere system. The recent follow-up email asked to see Planck curves for 255K and 288K (and to see them on a linear scale), so here is that graph:
The horizontal axis is wavelength in μm, and the vertical axis is energy in W/m2/μm.
There are three obvious features:
The "hotter source" explains why I used a logarithm scale in figure 2. The sun emits a lot more energy than the earth. There is also one more "feature" to figure 2: I scaled the solar output so that instead of giving the intensity at the surface of the sun, where it is emitted, I scaled it down to the value appropriate at the earth's orbit around the sun. That was the only way to get the two lines to graph anywhere close to each other.
So, if we look back at our discussion of the Beer-Lambert Law, what difference does the source temperature have on the absorption of IR radiation? (The original email had mentioned 15 μm, which we see is a little to the right of the peak in the above graph.)
Well, it turns out that the temperature of the source has absolutely no effect whatsoever on the absorption according to the Beer-Lambert Law.
Why is this? Well, there are several factors:
And all 15 μm photons are the same.
When CO2 absorbs a 15 μm photon in the atmosphere, it has no way of knowing if that photon was emtited from the surface at 288K, a kilometre away at 270K, or a metre away at 255K. It is just another 15 μm photon carrying the same amount of energy that every other 15 μm photon carries. And that amount of energy just happens to fit nicely into the different energy states that CO2 likes, so it is easy for CO2 to absorb it.
So, the CO2 will absorb the photon, and that heat is added to the local atmosphere, and it does not matter if the location where it is absorbed is warmer or colder than where the photon was emitted.
Boblaw @20, So it matters not what temperature the emitter was at, except that it governs the number of photons emitted. I was thinking of Wien's law that says the wavelength of the radiation is linked to the temperature of the emitter, so I was assuming that 15 μm radiation indicated 193K as the temperature of the emitter, meaning that radiation could only come from very cold places like the poles of the earth. Did I read Wien wrong?
Excuse me! Bob Loblaw. Brain out of gear!
Hello, Likeitwarm.
Yes, you are misinterpreting Wiens' law. It does not link a single photon to a specific temperature - it tells you the wavelength of the peak emission of all radiation from a blackbody as a function of temperature. You can read more about it here.
If you look at figure 2 of the blog post (or the non-log version for two IR temperatures in comment #20), you can see that Planck's Law tells us that any blackbody emitter, regardless of temperature, emits at all wavelengths. From those graphs, we can derive two interesting features:
If an object was at 193K, then the peak emission would be at 15 μm, but the body would still be emitting radiation at other wavelengths. At 255K, the peak emission would be at 11.4 μm, but the object would still be emitting at 15 μm, too - just not as much as at 11.4 μm.
All this is thinking in terms of blackbodies - perfect emitters. For gases, they do not tend to emit as blackbodies. You revise Planck's Law with a wavelength-specific emissivity. For a blackbody, the emissivity is always 1 for all wavelengths, leading to the curves in figure 2. In gases, the emissivity is rarely 1, and the emission curves are not nice smooth ones like figure 2. With many gases in the atmosphere emitting at many different wavelengths, you end up with curves that look like this. You can see that the measured spectral sort of follow the blackbody curves, with drops where atmospheric emissivity is less than 1.
(That figure is from this blog post.)
So, you have done the calculation correctly in Wien's Law, but misinterpreted it because it only applies to blackbody radiation, and it only tells us what the peak is. Once you factor in emissivity for a specific gas, we no longer have a blackbody, and the peak from a specific gas (e.g. CO2) is more a function of what wavelength has the highest emissivity. Even as the temperature of that gas changes, the wavelength with peak emissivity does not change, so knowing the peak emissiion can tell us what gas we are dealing with, but not its temperature. (At least, not without a lot of other information.)
[BL] 2022-08-06 image link fixed
Bob Loblaw @23
Thanks for clearing up my confusion. I thought 15 μm was only emitted from an object that was at the peak temperature, in this case 193K.
So, that means CO2 would receive the maximum amount of 15 μm at 193K?
From your example, 11.4 is a reduction from 15 by 24%. Would that mean there is a 24% reduction of 15 μm emission going from 193K up to 255K?
( I just don't like winter)
Well, no. It's more complex than that.
If you look at the diagram in comment 23, there are two sets of actual measurements - one looking up from the surface, and one looking down at an altitude of 20km. Let's think about what each one is looking at in more detail - but we'll pick the 15 μm wavelength as a single example.
I wrote the following over at another blog the other day, in response to someone else discussing the greenhouse effect.
With all these coupled layers absorbing, transmitting, and emitting, determining the flux of radiation requires a model of some sort. In the quoted text above, I referred to MODTRAN, which is one such model that you can read about - and try - online.
http://modtran.spectral.com/
http://climatemodels.uchicago.edu/modtran/
At the second link, the online model will let you choose a height, looking up or down, the temperature structure, etc. Lots to play with.
In short, a stream of 15 μm photons will be coming from a variety of distances away, at a variety of temperatures (and may have been emitted by something other than CO2). All we know about it is that they are 15 μm photons that all look the same to us.
Looking only at the emission at 15 μm, comment 20 shows the Planck curves for 288K and 255K. The (blackbody) values for each curve at 15 μm are 18.2 and 11.7 W/m2/μm.
If I do the calculation for 193K, the curve will be lower (and the peak further to the right), and the 15 μm emission drops to 3.4 W/m2/μm. The peak wavelength doesn't enter the calculation. The emissivity for CO2 will not be 1, but it will be more or less the same at the different temperatures, so you would expect a 193K cloud of CO2 to be emitting only 30% of the 15 μm photons you'd get from a CO2 cloud at 255K.
Just to make the text from comment 25 a little easier to understand, here is an updated version of the Planck curve graph from comment 20 - adding 193K as a third line.
In this figure, you can see how the peak emission shifts to shorter wavelengths at higher temperatures - 15 μm at 193K, 11.4 μm at 255K, and 10.1 μm at 288K. That's what Wiens Law tells us.
Notice that the 15 μm emissions are higher for 255K than for 193 K, and higher again for 188K - but the 15 μm wavelength is not at the peak for the latter two.
Wikkipedia have a Wein's Law page (aka Wein's Displacement Law) which may assist in the explanation.
Yes, that is a good page on Wien's Law. When I saw MA Rodger's comment, my first thought was "didn't I include that link in my previous comment?" - but I must have fogotten to add it. I was looking at it, at the time.
Useful article, but the example doesn't accurately reflect CO2 absorption. The example states that if you lost 1% of your energy through absorption in each cylinder, you would still have 37% of your ebergy after 100 cylinders. This is correct. But CO2 absorbs energy far more efficiently than that. Using the NIST data, the transmittance is only 30% through a 10cm path at 200mmHg. It's losing 70% of its energy, not 1%.
Granted, 200mmHg is far more CO2 than the atmospheric .300 mmHG of CO2 we're dealing with, but this means that an equivalent "cell" of absorption at 1 atmosphere with 400ppm CO2 would be 65.8m. After only 5 such "cells" you would have lost 99.76% of your energy to absorption.
We can discount re-radiation passing energy forward, as that's accounted for in the NIST measurements. The lost energy will be converted to heat, which will then conductively transfer to the other 99.96% of the gasses in the atmosphere, which will pass the energy upwards in their own spectral lines.
NO energy will be radiated into space in the CO2 absorption spectra - that atmosphereis completely opaque at those frequencies. Adding more CO2 won't change that. The idea that adding CO2 will change the characteristics of the re-radiation as it goes up the atmospheric column assumes that CO2 is the only gas, and that other gasses won't be conductively robbing the CO2 of the heat it's absorbed.
What WILL happen as CO2 levels increase is that the heat absorption will occur closer to the surface, causing an apparent increase in temperature, but this is offset by cooler temperatures at altitude, not accounting for convection and increased oceanic evaporation, which, while increasing the water vapor in the atmosphere (Major greenhouse gas) will also increase cloud cover and thus surface albedo, lowering the surface temperature of the ocean.
Scruffy:
As the article makes no mention of CO2, nor the length of the cylinders, when discussing the 1% per cylinder, 37% for 100 cylinders example in figure 4 and related text, your criticism of those numbers is a straw man argument. The example shows the exponential nature of the absorption relationship, and you are reading more into it than it says.
You do not explain what "NIST data" you are referring to. NIST is not mentioned in the blog post.
As for the rest of your comment, you have missed an extremely important factor. You speak of CO2 molecules absorbing IR radiation and transferring energy to other molecules. You seem to be completely unaware that the same process of molecular collision will add energy to CO2 molecules and allow them to continually emit IR radiation at the same wavelengths that CO2 absorbs IR radiation. Your conclusion that "no energy will be radiated into space in the CO2 absorption spectra" is simply wrong. For it to be true, CO2 molecules would need to drop to a temperature of 0K, which won't happen as long as they can collide with other molecules (of other gases) and maintain a tempesrature above 0K. In fact, they'll be at a temperature equal to those other molecules.
The bogosity of your argument is also made clear by your claim that other greenhouse gases can emit IR radiation "in their own spectral lines", and pass energy up through the atmosphere - energy that they received by collision with CO2 that absorbed IR radiation. This magical thinking requires that other gases follow different physics from CO2 - they can emit IR radiation, but CO2 can't. Standard physics does not claim that CO2 is the only gas that matters - it just accepts that all greenhouse gases can both absorb and emit IR radiation in the spectral lines that match their internal energy state levels. And that collisions are constantly transferring energy from one molecule to the next - in both directions (not just one, as your hypothesis requires).
You clearly do not understand how greenhouse gases play a role in atmospheric energy transfers.
Scruffy @29
Bob’s example illustrates the concept of a diminishing effect of increasing CO2, but as I challenged in @1 and Bob agreed in @2, it is insufficient to fully explain the complexity of the saturation effect. I prefer using the figure that Bob @7 reproduced from SpectralCalc.com for me to explain the saturation effect not as cylinders or cells in series, but as absorption lines (absorptance = 1 – transmittance) in parallel where strong lines reach an absorptance of 1.0 at low CO2 concentrations while weak absorption lines contribute to increasing absorptance with increasing concentration.
It is much better to interpret the Beer-Lambert Law by looking down at the atmosphere from space than it is to look up from the surface. The common view of Beer’s Law considers attenuation of the energy emitted from a surface. For example, measure the energy emitted from a source, travels through gas such as CO2, and reaches the end of a cell. The NIST spectrum provides the results for the specified set of conditions using this approach. However, the energy that reaches the end of the cell from the original source does not include re-radiated energy. That is because IR absorbed by CO2 in the cell is re-radiated in all directions, mostly to the cell walls where it is absorbed by the cell walls. The geometry of the measurement cell, unlike the open atmosphere, precludes re-radiated energy.
You say “NO energy will be radiated into space in the CO2 absorption spectra - that atmosphere is completely opaque at those frequencies.” This should be clarified to say that none of the original source energy (photons) from the surface will be radiated into space because it will be absorbed and re-radiated along the path length toward space. However, all molecules above absolute zero vibrate and radiate energy. CO2 at all levels of the atmosphere will radiate energy. At the uppermost atmospheric layer containing sufficient CO2 molecules, energy radiated by CO2 will radiate to space in the CO2 absorption band, precisely because absorption lines have a value great than 0. Kirchhoff’s Law provides that absorptance = emittance (with the caveat of being at thermal equilibrium, which allows for energy transfer between molecules by collision or conduction in addition to radiation.)
Bob’s experiment in the original post demonstrates why it is better to view the effect of Beer’s Law on radiant energy escape to space by looking down from space. The atmosphere in the tropopause at an altitude of about 10-20 km is thin and cold. There is a lot of distance between CO2 molecules. The key is that there is a very long path length available, sufficient to bring many of the absorptance lines in the CO2 band to 1.0. With increasing CO2 concentration, even the absorptance of very weak lines becomes significant.
Your description of the overall global heat balance is incorrect. Increasing CO2 will cause more heat to be absorbed closer to the surface, and this will lower the temperature of the tropopause. This is part of a special and complicated signature of global warming by CO2. It actually reduces emittance to space, aggravating the greenhouse effect rather than offsetting it. The greenhouse effect is driven by the temperature profile of the upper atmosphere. What happens in the troposphere below the tropopause, including convection, conduction evaporation, and condensation, just moves heat around within the troposphere. You mention the effect of water vapor, which also exacerbates global warming as a positive feedback effect. The role of clouds is complicated. High, cold cirrus clouds can increase warming while low, warm, thick clouds can reflect solar energy. All of this is discussed in detail elsewhere, and is beyond the scope of a single rebuttal. But if you have any more specific questions that are stumbling blocks for your understanding, I will try to address them as succinctly as possible.
Why, you might ask, did I say "it is much better to interpret the Beer-Lambert Law by looking down"? Because it determines whether there are enough molecules in the path length to create a layer that emits toward space with an emittance close to 1.0. And it avoids the confusing discussion of absorption and re-emittance, which is unnecessary to understand radiant energy loss to space.
For example, in the wavelength range of about 14-16 microns, Beer’s Law determines that there are enough CO2 molecules in the very long path length of the tropopause (altitude 10-20 km) to bring most absorption lines in this band to 1.0, even with a low concentration of 400 ppm and even with the low pressure of the tropopause. CO2 creates an effective emitting layer in this wavelength range. Because the tropopause is cold at 217K, this layer emits less energy compared to that emitted in this range from the surface at 288K. In the ranges of 8-9 and 11-13 microns, there are no gas molecules that absorb radiant energy, so the energy emitted from the surface (288K) reaches space. Without CO2 reducing energy escape to space, the earth would be cooler while maintaining the energy balance with solar insolation. With increasing CO2, more weak absorption lines in the ranges of about 13.5-14 and 16-16.5 microns increase toward a value of 1.0 and the absorption band becomes wider, requiring a higher surface temperature to maintain the overall global energy balance.
Regarding water vapor, there are not enough molecules in the cold tropopause to create an emitting layer. The emitting layer for water vapor in the troposphere is warmer.
Charlie Brown's comment about using the Beer Lambert Law "looking down" is an interesting point worth following up on.
Absorption is a probability thing. When we say that a layer absorbs 1% of the radiation emitted from the surface, we are talking about the average of a huge number of photons. For a single photon, the proper interpretation is that the photon has a 1% chance of being absorbed in that layer, and a 99% chance of being transmitted.
For the view looking down from the top of layer 200 in Figure 5, reverse the X-axis so that 200 is on the left and 0 is on the right, and we can re-interpret the graph as "what is the probability that we will see a photon that originated in layer 200? 150? 100? etc. Photons that start in layer 199 have a really high probability of reaching layer 200 and being transmitted through it. Layer 190? Better than 50% for the two absorption coefficients used in the graph. Layer 180? Chances are only 10-35% for the two coefficients.
So, the IR radiation emitted by CO2 and lost to space more likely comes from the upper atmosphere.
Any "argument" that claims the CO2 effect is "saturated", etc., because surface-emitted radiation won't directly reach space needs to explain why they think the rest of the atmosphere is not emitting IR radiation from CO2.