The anthropogenic global warming rate: Is it steady for the last 100 years?
Posted on 11 April 2013 by KK Tung
This is a guest post by KK Tung, who requested the opportunity to respond to the SkS post Tung and Zhou circularly blame ~40% of global warming on regional warming by Dumb Scientist.
The observed global-mean temperature has gone through a number of ups and downs since 1850, which is the beginning of the available global temperature record. Our recent paper of Tung and Zhou [2013] in Proceedings of National Academy of Science (PNAS) was the latest among a large body of published literature on the evidence of a multidecadal oscillation that can be seen in the global-mean surface temperature record. We further reported a quantitative analysis (multiple linear regression (MLR)) using the global (not regional) temperature data (HadCRUT4) that attributed a warming rate of 0.07-0.08 °C/decade to net anthropogenic forcing. That warming rate has been steady for the past 100 years, through the ups and downs of about 30-year duration, which we attributed to the Atlantic Multi-decadal Oscillation (AMO). In this view, the anthropogenic warming has not stalled in the past decade and half, nor has it accelerated in the previous three decades. I thank Skeptical Science for giving me this opportunity to explain in a more understandable way some underlying issues that have caused confusion to nonspecialists.
(1) Greenhouse gas concentration vs expected warming
How can the anthropogenic warming be approximately linear in time when we know that atmospheric CO2 has been measured to increase almost exponentially? Implicit in that statement is the expectation that the warming (i.e. the rate of surface temperature increase) should follow the rate of increase of greenhouse gas concentration in the atmosphere. This rather common expectation is incorrect. An accessible reference is that from Britannica.com: “Radiative forcing caused by carbon dioxide varies in an approximately logarithmic fashion with the concentration of that gas in the atmosphere. The logarithmic relationship occurs as the result of a saturation effect wherein it becomes increasingly difficult, as CO2 concentrations increase, for additional CO2 molecules to further influence the ‘infrared window’ (a certain narrow band of wavelengths in the infrared region that is not absorbed by atmospheric gases)”.
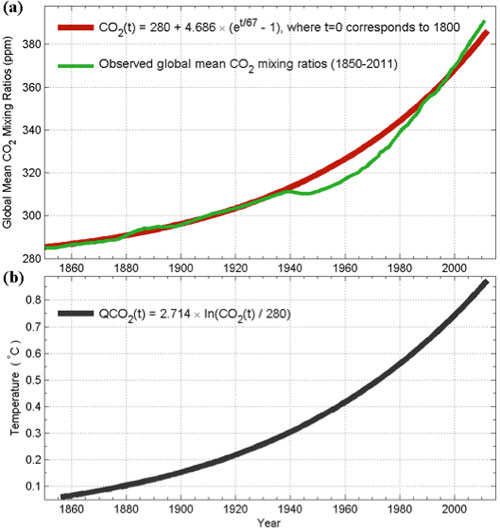
Figure 1. (a) the measured atmospheric concentration of carbon dioxide in green and the fitted smooth function in red. (b) the logarithm of the red curve in (a). The constant multiplier in front converts it to the global mean temperature; details of that MLR analysis are not discussed here to avoid confusion.
Figure 1a shows that the well measured CO2 concentration (in green) can be fitted to an exponential function plus a constant preindustrial value (in red). So it is true that one can claim that the carbon dioxide concentration in the atmosphere has increased at an exponential rate. Normally the logarithm of an exponential function in time is linear in time. However the fit of CO2 has a constant in additional to the exponential, and so its logarithm is slightly more curvy than linear. Nevertheless it can still be regarded as almost linear over multidecadal intervals to within 0.1 °C. Logarithm of that function is shown in Figure 1b as QCO2, which represents the radiative heating from CO2. The exponential growth of the CO2 after 1950 is much muted in the logarithm (taking into account the fact that the vertical scale is in small 0.1°C increments.
The real situation is more complicated than indicated by these simple functions, because the net anthropogenic forcing is the sum of radiative heatings from individual greenhouse gas concentrations and tropospheric sulfate aerosol cooling (man-made pollution). We show in Figure 2a the sum of radiative heating from all well-mixed greenhouse gases in green and the sum of radiative cooling from tropospheric aerosol effects in blue. Because some of the greenhouse gases such as methane are more powerful radiatively than carbon dioxide, one cannot simply take the logarithm of the sum of the greenhouse gas concentrations to arrive at the total heating rate from them. They need to be calculated individually. These calculated radiative heating rates are available from NASA's Goddard Institute for Space Studies (GISS) at http://data.giss.nasa.gov/modelforce/, and have been used in the GISS model, one of the models participating in IPCC studies. As shown in Figure 2a, the green line is quite nonlinear and shows the acceleration of greenhouse gas forcing after 1950 referred to by DS, but the aerosol cooling also increased after 1950. The net anthropogenic forcing is the small difference of the two large terms. The near cancellation by the two anthropogenic components may be one of the explanations of why the warming deduced by Tung and Zhou is smaller than the response expected from greenhouse gas warming alone. Because the aerosol cooling part is uncertain, we actually do not know what the net anthropogenic forcing looks like. There is no obvious argument that one can appeal to on what the expected warming should be. There is nothing obviously wrong if the anthropogenic warming is found to be almost linear in time. This is the first point I would like to make.
(A side comment: Depending on the exact form of the aerosol cooling adopted, the net anthropogenic forcing is different from model to model. Although you probably cannot see it just by eye-balling the two curves in Figure 2a, their difference actually is nonlinear, with accelerating heating after 1978, allowing the GISS model to produce the accelerated warming after 1978 from anthropogenic forcing alone. Other groups adopt somewhat different time dependent shape of net anthropogenic forcing. See here and here.
Analysis of models by several authors showed that there was a large range of net anthropogenic forcing adopted by models participating in IPCC assessment reports, with a tendency for the models with higher climate sensitivity to adopt a lower net forcing and less sensitive models to adopt a higher net forcing.)
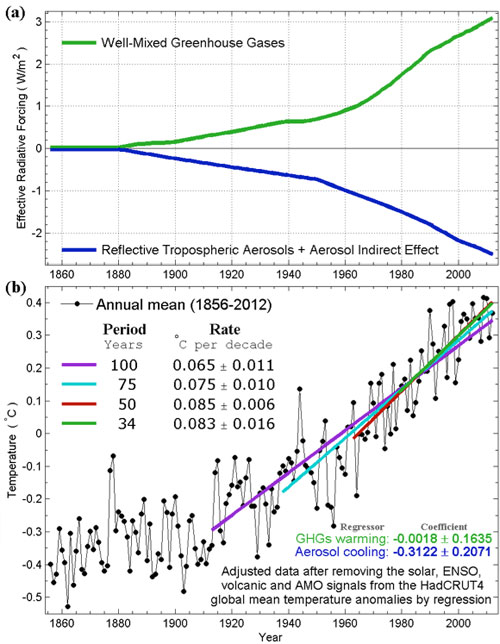
Figure 2. (a) Radiative forcing of various anthropogenic components. (b) Results of Multiple Linear Regression using natural and anthropogenic regressors. Adjusted temperature, which is the same as the combined response to the anthropogenic forcing plus the Residual is shown. This multiple linear regression using two highly collinear regressors is not recommended, but nevertheless yields approximately the same result for the adjusted temperature trend.
(2) “Circular argument”?
One common way to deduce the anthropogenic warming signal from observed data is to remove all other known natural influences, such as El Nino, volcanic aerosols, solar forcing (cyclic and secular) and the AMO. These are called the predictors or regressors. What remains are random climate noise, and the net anthropogenic warming rate. We call the sum of the two the “adjusted data”, following Foster and Rahmstorf [2011] . The MLR model for the observed temperature T(t) is:
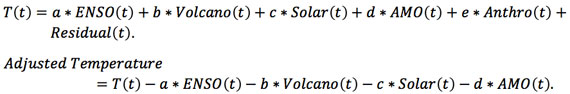
The MLR procedure assumes the form for the predictors and tries to fit the observed temperature with them using the least-squares best fit. The model is successful if the procedure yields a Residual(t) that contains only climate noise, but often it also contains some trend. When that happens it is telling us that the assumed trend in the anthropogenic component (e*Anthro(t)) is probably not correctly giving the anthropogenic trend consistent with the observed temperature.
The adjusted data can be viewed as the temperature with natural variations removed. Because the adjusted temperature can also be expressed as
![]()
the deduced anthropogenic trend can be corrected by adding the trend in the Residual to e*Anthro(t). It turns out that this trend deduced from the Adjusted temperature is not always the same that in e*Anthro(t). This procedure of deducing the trend from Adjusted temperature is actually not sensitive to the assumed form of Anthro(t), as long as it has a long-term trend: When the assumed Anthro(t) has a too large a trend after 1978 compared to before 1978, for example, the Residual (t) will show a negative trend after 1978 and a positive trend before that time. See the example discussed in Zhou and Tung [2013] . Since we do not know a priori what the form of net anthropogenic forcing is because of its large uncertain tropospheric sulfate aerosol component, to be agnostic we used a linear function for Anthro(t) in the intermediate step as a “placeholder”. That was probably the source of the circular argument criticism from DS: “Tung and Zhou implicitly assumed that the anthropogenic warming rate is constant before and after 1950, and (surprise!) that's what they found. This led them to circularly blame about half of global warming on regional warming.” It is important to note that the trend we were talking about is the trend of the Adjusted data, and not the presumed anthropogenic predictor.
We will next show that we get approximately the same result using more nonlinear placeholders for the anthropogenic predictor. In the first example, we proceed to do a MLR analysis using the two anthropogenic predictors: one the nonlinear green line and the other the blue line in Figure 2a, and let the MLR procedure adjust the proportions of the two to get a best fit. This is probably what nonspecialists would find most natural and expect us to do (but specialists know not to do). After the multiple regression analysis is done, the adjusted data is reconstructed by adding the residual to the sum of the two regressed anthropogenic responses. This is shown in Figure 2b. The regression coefficient of greenhouse gas warming is shown as “warming” and the aerosol cooling is shown as “cooling”. The multiple regression analysis is confused by the two highly correlated anthropogenic regressors (this is the well-known problem of collinearity), producing a “warming” that is negative and a “cooling” that is positive. This is not surprising given how close the two curves look in Figure 2a. Nevertheless, the combination of the two responses is robust. When combined to yield the adjusted data, the 100-year, 50-year and 34-year linear trends are still rather steady at ~0.07-0.08°C/decade as shown by the dots in Figure 2b and the trends fitted through them. The result is very close to that found in Tung and Zhou [2013] using a linear predictor as a placeholder. We have tried many other predictors with similar results. Using a nonlinear anthropogenic regressor would still yield an almost linear trend for the past 100 years, if the Residual is added back. And so this procedure is not circular. This is the second point I am trying to make.
Of the different regressors we tried the single anthropogenic regressor that is closest to the final adjusted data turns out to the QCO2(t) function given in Figure 1b. This is shown in Figure 3. The difference between the adjusted data and the QCO2 regressor is the Residual, which is shown in the inset. Except for s a minor negative trend in the last decade in the Residual, it is almost just noise. So the MLR with QCO2 as the anthropogenic regressor is successful. That small negative trend in the Residual, when added back to QCO2, yields a more linear trend in the adjusted data, similar to what we found in Tung and Zhou and in Figure 2b here. (The physical interpretation of why the net anthropogenic warming appears to follow the radiative heating by CO2 alone and with so little lag between forcing and response is rather tricky and will not be discussed here.)
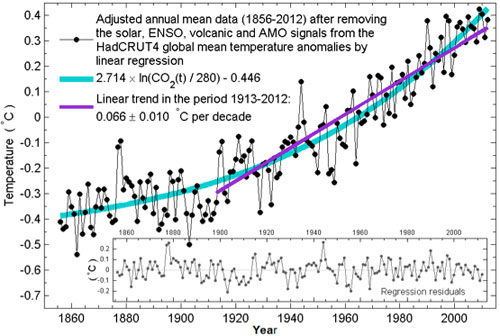
Figure 3. Adjusted data shown in dots, obtained by a MLR using QCO2 as the anthropogenic predictor. The QCO2 is superimposed. The Residual is shown in the inset
(3) “Don’t explain the physics”?
Because of the page limitation of PNAS, a review of the physics of the AMO by other researchers is necessarily brief, with fuller discussions given in the references quoted. Even so, our PNAS paper has the following paragraph on the physical mechanism of the AMO, which Dumb Scientist apparently missed: “The phenomenon likely involves thermohaline circulation variability in the Atlantic Ocean. As described in Dima and Lohmann [2007 ]; Semenov et al. [2010] , the negative feedbacks between the strength of the thermohaline circulation which brings warm sea-surface temperature (SST) to the North Atlantic, and the Arctic ice melt in response to the warm SST, which, because of reduced deep-water formation, then slows the strength of the thermohaline circulation after a delay of 20 years, together create the restoring force responsible for the oscillation. Recently a 55-80-year AMO has been model simulated as arising from the variability of the meridional overturning circulation in the Atlantic Wei and Lohmann [2012] .”
As I have now exceeded the recommended length for the post, I hope in a second post to give a more detailed review of the physical mechanisms of the AMO (noting that the science is not yet settled), its relation to the Atlantic Meridional Overturning Circulation, the choice of the AMO Index (whether the detrending should be point by point or by the global mean), and why the claim that the observed multidecadal variability can be simulated using time-varying aerosols may not be consistent with the observed data.
References
Dima, M. and G. Lohmann, 2007: A Hemispheric Mechanism for the Atlantic Multidecadal Oscillation. Journal of Climate, 20, 2706-2719.
Foster, G. and S. Rahmstorf, 2011: Global temperature evolution 1979-2010. Environmental Research Letters, 6, 1-8.
Semenov, V. A., M. Latif, D. Dommenget, N. Keenlyside, A. Strehz, T. Martin, and W. Park, 2010: The impact of North Atlantic-Arctic multidecadal variability on Northern Hemisphere surface air temperature. J. Climate, 23, 5668-5677.
Tung, K. K. and J. Zhou, 2013: Using Data to Attribute Episodes of Warming and Cooling in Instrumental Record. Proc. Natl. Acad. Sci., USA, 110.
Wei, W. and Lohmann, 2012: Simulated Atlantic Multidecadal Oscillation during the Holocene. J. Climate, doi:10.1175/JCLI-D-11-00667.1.
Zhou, J. and K. K. Tung, 2013: Deducing the multi-decadal anthropogenic global warming trend using multiple regression analysis. J. Atmos Sci, 70, 3-8.































 Arguments
Arguments






























Reply to post 49 and 50; By "almost" I didn't intend to imply more or less. The exponential function was used in my figure 1 to show that it almost fits the actually data. In the calculation done in Figure 2, the actual emission was used to calculate the radiative forcing. So this distinction of more or less than exponential is moot.
Thank you Dr Tung for engaging here about your paper.
It is an interesting analysis, but the results are strongly dependent on the assumed shape of the anthropogenic signal. This signal is not properly approximated as linear from 1850 onwards (see e.g. fig 8.18 of the AR5 SOD or similar figures). This is in contrast to the past three decades as analyzed by Foster and Rahmstorf, where the linear approximation is much more valid.
By assuming linearity, the non-linear part of the anthropogenic forcing will be incorrectly attributed to the AMO.
See also this attempt to reproduce the results in the paper, but then using the time evolution of CO2 concentrations instead of a linear trend as a proxy for the anthropogenic forcing: http://www.staatvanhetklimaat.nl/2012/10/26/is-the-amo-the-explanation-for-the-1940-1970-temperature-standstill/
Obviously, this is still a very incomplete analysis, since the net anthropogenic forcing is not properly represented by the CO2 concentration (because of the logarithmic relationship and because of other forcings being also important), but it shows the strong dependence of the results on what is assumed to be the anthropogenic signal. The anthropogenic warming trend is seen to accelerate with this slightly better (though still flawed) assumption.
An improved (and very interesting) analysis would take the net anthropogenic forcing as the anthropogenic signal. If the AMO index can be properly detrended for such an analysis is questionnnable: All other tempoerature influences would have to be subtracted, and those temperature influences are actually what one is after with such an analysis. The detrending thus invariably involves either dubious or highly uncertain assumptions or circulair reasoning. The latter could perhaps be ameliorated by an iterative analyis.
Another approach would be to rather than using a questionnnable (see my previous commment) estimate of the AMO as a predictor in the regression analysis, see if there is a AMO-type (or other cyclical) signal is left over in the adjkusted temperature, after having corrected for the better known influences (solar, ENSO, volcanic, anthropogenic).
The Lean and Rind analyses would make me think there would not be a substial influence of such cyclical behavior, but that's worth investigating with newer data.
In reply to posts 52 and 53 by Bart Verheggen: Your suggestions are fair. Our work were actually following ideas similar to your suggestions.
(1) We did not assume linearity for anthropogenic forcing. In the post we used a number of nonlinear anthropogenic indices.
(2) "Another approach would be to rather than using a questionnnable (see my previous commment) estimate of the AMO as a predictor in the regression analysis, see if there is a AMO-type (or other cyclical) signal is left over in the adjkusted temperature, after having corrected for the better known influences (solar, ENSO, volcanic, anthropogenic)." This was what we did in Zhou and Tung (2013). After we accounted for your suggested better known influences, the blue line in the figure was what remains, and it shows an AMO like signal.
[image snipped]
[Dikran Marsupial] Sorry, I had to delete the image as it was causing formatting problems (at least under Firefox). Please try using a URL to a copy of the image that already exists on-line.
Could someone tell me how to insert a figure into the comment the correct way? Thanks.
Also in reply to post 53: "The Lean and Rind analyses would make me think there would not be a substial influence of such cyclical behavior, but that's worth investigating with newer data". This was done with the old and also with the new data. See my post above. The point is: if you just look at the anthropogenic response from the assumed regressor, it would show accelerated warming after 1978. But the residue has a negative trend after 1978. When that negative trend is added back to the regressed response, the combination becomes more linear.
Here is another try for post 54 with a pdf figure:
I am glad that it (inserting a figure) works this time!
This figure was done following Bart Verheggen's prescription of removing the usual solar, ENSO and volcano influences, but not the AMO or anthropogenic influence, because we don't know what the latter is.
I thought I would have a go at testing Prof. Tungs method via a simple thought experiment, where we can have ground truth. I've used MATLAB, so I'll add code snippets and diagrams as I go. I should however point out that it is possible that I have misunderstood the method, in which case hopefully setting things out very explicitly will help Prof. Tung to identify where i have gone wrong.
Lets assume that that anthropogenic emissions have been rising quadraticaly
anthro = 0.00002*(T + T.^2);
where T is time and goes from 1 to 150 years in the diagrams shown below. Rather than model ENSO, volcanic activity and solar forcing separately, for convenience, we can lump them all together as a single term "natural", and we will make it sinusoidal to keep things simple.
natural = 0.1*sin(2*pi*T/150);
For the sake of this thought experiment, I shall assume that AMO actually has no effect at all on global mean surface temperatures, so the observations are an equal combination of anthro and natural and some additive Gaussian noise
observations = anthro + natural + 0.1*randn(size(T));
Now lets assume that AMO is actually a consequence of anthropogenic and natural forcings/variability, so it is correllated with the observations, but only because the observations and AMO have shared causes.
AMO = 0.4*anthro + 0.6*natural;
Now this presents a stren test for Prof. Tung's method, but if his method is sound, it ought to still be able to deduce the correct anthropogenic forcing even in this case. If we plot everything, we get this:
Note I have set up my thought experiment, so the observations are vaguely similar to the actual observations.
The next step is to linearly detrend AMO, which can be easily achieved via linear regression:
X = [ones(size(T)), T];
beta = (X'*X)\X'*AMO;
AMOd = AMO - beta(2)*T;
Plotting the detrended AMO gives this:
Now linear detrending obviously does not remove the all of the effects of anthro from AMO as anthro is quadratic. Also if natural has a linear trend over the period considered, then that also will have an effect on the detrending.
We can now perform the regression analysis, where the means have been subtracted from the explanatory variables so that any offset in the observations are explained by the bias term, rather than using the explanatory variables.
X = [ones(size(T)) anthro-mean(anthro) natural-mean(natural) AMOd-mean(AMOd)];
beta = (X'*X)\X'*observations;
We can look at the values of beta that we have extracted, and we find
beta = [0.1577; 0.6382; 0.1927; 1.1731]
Note that the regression model is using AMO to explain more of the variation in the observation than it uses anthro or natural, even though the observations are in no way causally dependent on AMO! The true set of regression parameters are:
beta = [0.1577; 1.0000; 1.0000;0.0000]
We know that by construction. This is a good illustration of why using regression methods for attribution is tricky. In this case, the problem is co-linearity. AMOd is correlated well with the observations, in face more so than anthro or natural are individually, and regression is a correlation based method.
We ccan then find the output of our regression model
model = X*beta;
and plot it, giving
So we can see that the regression model (blue) "explains" the observations (green) almost as well as the true model does.
The last step is to find the deduced anthropogenic forcing. My interpretation of Prof. Tungs explanation given in the post above is that we first find the residuals
residual = observations - model;
compute their least-squares trend
X = [ones(size(T)), T];
BETA = (X'*X)\X'*residual;
and adding the trend in the residuals to the deduced anthro
infanthro = beta(2)*anthro + BETA(2)*T;
but if you do that, you get
where you can see that the deduced anthro is much less than the true anthro, which suggests that Prof. Tungs method is not reliable.
UPDATE: If we exactly deduct the anthropogenic influence on the AMO using
AMOd = AMO - 0.4*anthro;
then we get more or less the correct answer:
which suggests that the way in which the anthropogenic influence on the AMO is accounted for is very important, and linear detrending is unsatisfactory unless the anthropogenic forcing actually is linear.
I have also noticed that in both cases, the trend of the residuals is to all intents and purposes zero, so adding the trend of the residuals to a*anthro(t) as Prof. Tung suggests has only a negligible effect on the outcome.
Now I should stress, there are at least two possible explanations, either (a) Prof. Tung's method isn't reliable or (b) I have not propely understood or implemented Prof. Tungs method for my thought experiment. I try to be a self-skeptical sort of person, so I am assuming (b) is more likely. Hopefully Prof. Tung can point out the problem, providing MATLAB (or other) code for the thought experiment would be a really good way of getting his idea accross efficiently.
[Dikran Marsupial] Oops, one error found already,
infanthro = beta(1)*anthro + BETA(2)*T;
should of course have been
infanthro = beta(2)*anthro + BETA(2)*T;
The penultimate figure has been updated to take this into account, sorry for the confusion.
Thanks Dikran! I have to rush off to a talk, but I wanted to nitpick: our CO2 emissions are rising faster than exponentially. Anthropogenic forcings might be rising quadratically...
Dumb Scientists yes I agree, however we need to determine if the basic approach is mathematically sound before worrying too much about the details!
As an update to my previous post on Prof Tung's method, I've now investigated quadratically detrending the AMO signal to remove the anthropogenic influence, using:
X = [ones(size(T)) T T.^2];
beta = (X'*X)\X'*AMO;
AMOd = AMO - X*beta;
This doesn't work either, but this time it over-estimates the anthropogenic forcing, although the error is smaller than for the linear detrending.
The reason this doesn't work either is both subtle and interesting. Ideally the detrending would eliminate the quadratic anthropogenic component leaving only the sinisoidal natural component. However, the sinusoidal component has a linear trend, being positive in the first half of the time series and negative in the second. So when we quadratically detrend the raw AMO signal, we can erase both the anthropogenic component AND the linear component of the natural signal. However the linear component of the natural signal slopes downward and that of the anthropogenic signal upward, so this cancels out to a degree, and the resulting quadratically detrended AMO signal has an upward linear trend.
We defined the synthetic AMO signal as
AMO = 0.4*anthro + 0.6*natural;
so if we exactly remove the anthropogenic component, the correctly detrended AMO signal is just 0.6*natural (blue). However if we use simple quadratic detrending, we get the AMOd signal shown in red. The green line just shows the difference between the two.
The problem is now that the component shown in green is correllated with the anthropogenic component of the observations, so a quadratically detrended AMO still acts as a proxy or alias for BOTH the natural and anthropogenic components of the observations, which means that you can't use this method for attribution either.
The bottom line is that it seems that Prof. Tung's method only gives the correct answer if the anthropogenic component is exactly removed from the AMO signal before performing the regression. Adding the trend of the residuals does not solve this problem. Of course we can only exactly remove the anthropogenic component from AMO if we already know what it is, so using this method to estimate the anthropogenic component of the observations does require circular reasoning... provided I have not misunderstood the method, of course!
Dikran Marsupial @57.
Assuming your method holds up, you have illustrated that by subtracting the AMO signal from global temperature to reveal the AGW, you can be also inadvertantly be subtracting a significant amount of AGW. Your "Question 2" @16 thus stands now with evidential support.
Commendable stuff but....
The question that would perhaps follow would concern whether the proportions shown within the example you present (ie that 33% of the AGW signal is lost by subtracting AMO in this manner) are sensitive or insensitive to the situation. Will it always be about 33% or will it sometimes be much more, or less.
And I am far more sceptical about T&Zh13., I feel this chipping away is not the best approach. Indeed I remain sceptical that there can be any significant contribution to the global temperature anomaly from AMO.
One point I would make runs as follows - If global temperature wobbles 0.3ºC peak-to-peak due to AMO (as T&Zh13 asserts) and if 67% of this is resulting naturally from AMO (ie if we factor in the suggested finding @57 = 0.2ºC) then how much energy will be required to wobble the global temperature that amount? With TRC=2ºC (this is one place where contrarians would find high Climate Sensitivity useful), the global wobble would require a forcing equatable to 10% of 2xCO2 or 0.37Wm^-2 or an energy flux of 6ZJ pa. If this energy flux originates solely in the N Atlantic (ie if it is a direct energy output of the AMO), it will incur significant losses as it spreads out around the world. If the AMO has some deliverable other than 'heating of the climate' then the T&Zh13 thesis has some explaining to do.
I think I will go in search of my 6+ZJ pa. It is rather a large quantity to go unnoticed.
I suppose my feeling on all this is that the AMO is simply an ocean waggling like a continent and is driving zip. But such comment here is pure speculation. And I am prepared to admit as much.
MA Rodger The degree to which Prof. Tung's method over- or under-estimates the true anthropogenic component depends on both the true "noise" (the variation not due to the factors explicitly included in the model - note this is not necessarily the same as the residuals from the regression) and on the nature of the non-anthropogenic factors. As linear and quadratic detrending are correllation based methods, they are highly susceptible to any correlation or anti-correlation between the anthropogenic and non-anthropogenic components of the AMO. Similarly any flaw in the detrending of the AMO that is correllated or anti-correlated with the noise in the observations may be exploited by the regression procedure.
Essentially Prof. Tung's regression approach appears only to be workable if we can eliminate the anthropogenic influence on AMO exactly without attenuating any of the non-anthropogenic component. We can't do this unless we already know what exactly the anthropogenic influence on AMO actually is. I don't think this is "chipping away"; if my analysis turns out to be correct (and I have no problem with being wrong - it is part of normal scientific procedure!) then the whole regression procedure is invalid and hence does not support the conclusion.
Even when valid, regression methods can only really show that something CAN BE explained by something else, not that something IS explained by something else. We really need physics to determine whether AMO actually does influence GMST. The work of Foster and Rahmstorf shows that we don't need AMO to explain the "hiatus" as it CAN BE explained using ENSO etc. Occam's razor suggests we shouldn't needlesly introduce new elements if an existing theory already explains the observations already; however that doesn't mean that AMO has no effect on GMST.
Dikran Marsupial @62.
I can agree almost fully with your comment. Perhaps the use of Occam's razor needs wielding with care so it doesn't become Occam's broom (sweeping stuff under the carpet, out of sight).
The point with the 'chipping away' idea is that just as CAN BE is distinct from IS, so it is also distinct from IS NOT. Thus, while our inabilities in removing the AGW signal from AMO would seemingly present an insurmountable problem for the T&Zh13 method, the question of how much of recent global warming is AMO and not AGW will remain unanswered.
So I'm thinking of looking to see if there are signs of AMO warming beyond the N Atlantic, or signs of non-AMO warming. A tiny bit of harmless analysis. But frankly analysis that I feel should have been done already. Perhaps it has & I missed it. Perhaps not.
So where to look for evidence of AMO warming beyond the shores of the N Atlantic?
My first thought was that if AMO was going to effect temperatures anywhere, it would be the UK. Indeed, the CET was invoked within T&Zh13. So I compared CET with the SST for the surrounding seas (45-65N, 20W-10E) with nomad3 providing monthly SST data - 1981 to date. The two temperature profiles are re-based for comparison and graphed below. with AMO also plotted (although AMO is of course subject to a de-trending).
The divergent record is evidently CET not the SST which suggests that during these divergent periods, AMO is not in any way a dominant influence in CET. So are divergent periods infrequent such that the period 1988-2004 is the norm where SST & CET can be married together?
A de-trended CET for the period of Enfield's AMO index (1856 to date) is next up for comparison being graphed below. Divergence appears the normal state here, with the two indices have little in common. I would conclude that the CET record does not support the suggestion that AMO drives UK temperatures.
Still. It's early days. There may yet be that local variation is swamping the signs of the AMO driving UK temperatures. And the UK is not the whole globe.
I continue my game of cosmological Where's Wally by crossing the Atlantic. The US Eastern seaboard stretches 1,500 miles so can provide a regional temperature by averaging a set of State data from NCDC, Maine, Massachusetts, Maryland, N Carolina & Florida being chosen. They have a very similar temperature record as shown in the tiny inset graphic. (The anomaly base 1895-1945 is probably the reason for the particularly close match during those years.)
The contiguious ocean SST from nomad3 were taken as 25-45N, 70-80W. (This isn't the most representitive part of the Atlantic SST-wise, lacking signs of warming 1981-date.) AMO is after Enfield.
The first graph shows the land & adjacent ocean temperatures 1981-date do have certain similarities but with warming only evident on land. Also, if the larger wobbles match up, they appear a month or so earlier on land, which is not good for any theory of AMO as a driver of land temperature.
The second graph attempts to compare those US temperature records with AMO over a 120 year period. I see there no evidence of AMO warming the Eastern coast of the USA over that period.
So where is Amo hiding?
Link for above image
Link for above image
[DB] Added links to the images themselves, as they will not display directly due to limitations in how Google stores them.
I wanted to thank Dikran again for his contribution. It inspired my own simulation, which has better formatting here.
Apologies for the non-functioning links @64 & @65 & thank you DB for providing links.
I feel the extra palaver of linking to view the graphics is a step too far so will attempt to find a host for the graphics that will allow on-page viewing.
So where to look for evidence of AMO warming affecting climate beyond the shores of the N Atlantic?
My first thought was that if AMO was going to effect temperatures anywhere, it would be the UK. Indeed, the CET was invoked within T&Zh13. So I compared CET with the SST for the surrounding seas (45-65N, 20W-10E) with nomad3 providing monthly SST data - 1981 to date. The two temperature profiles are re-based for comparison and graphed below. with AMO also plotted (although AMO is of course subject to a de-trending).
The divergent record is evidently CET not the SST which suggests that during these divergent periods, AMO is not in any way a dominant influence in CET. So are divergent periods infrequent such that the period 1988-2004 is the norm where SST & CET can be married together?
A de-trended CET for the period of Enfield's AMO index (1856 to date) is next up for comparison being graphed below. Divergence appears the normal state here, with the two indices have little in common. I would conclude that the CET record does not support the suggestion that AMO drives UK temperatures.
Still. It's early days. There may yet be that local variation is swamping the signs of the AMO driving UK temperatures. And the UK is not the whole globe.
I continue my game of cosmological Where's Wally by crossing the Atlantic. The US Eastern seaboard stretches 1,500 miles so can provide a regional temperature by averaging a set of State data from NCDC, Maine, Massachusetts, Maryland, N Carolina & Florida being chosen. They have a very similar temperature record as shown in the tiny inset graphic. (The anomaly base 1895-1945 is probably the reason for the particularly close match during those years.)
The contiguious ocean SST from nomad3 were taken as 25-45N, 70-80W. (This isn't the most representitive part of the Atlantic SST-wise, lacking signs of warming 1981-date.) AMO is after Enfield.
The first graph shows the land & adjacent ocean temperatures 1981-date do have certain similarities but with warming only evident on land. Also, if the larger wobbles match up, they appear a month or so earlier on land, which is not good for any theory of AMO as a driver of land temperature.
The second graph attempts to compare those US temperature records with AMO over a 120 year period. I see there no evidence of AMO warming the Eastern coast of the USA over that period.
So where is Amo hiding?
(The previous graphs illustrating Where's Amo? should now also be visible.)
A selection of US States can also be used to create a temperature profile for a North-South band of the country. This is done here to create 4 more temperature records westward across the US. (Eg (1) Ohio, Kentucky, Tennessee, Alabama. (2) Minnesotat, Iowa, Missouri, Arkansas, Louisiana. (3) Montana, Wyoming, Cloorado, New Mexico. (4) Washington, Oregon, Calafornia.) With one exception, the individual state data in each N-S band again provide similar temperature records (the exception being Montana which experiences a cold spell all of its own in the late 40s-early 50s). (The data all has the same E Coast 'de-trending' trend subtracted from them for sake of the comparison.)
The graph below is rather busy but still gives no indication of AMO affecting US temperatures. The 'saw-tooth' profile of the East coast actually amplifies beyond the Appalachians but disappears by the Rockies where, if you really want it to be there, the profile looks a bit like AMO. But, no, it is gone by the West Coast. So Where's Amo?
When the US average temperature anomaly is plotted, something a little like AMO starts to appear with a strong amplitude, stronger than AMO. However it still remains different enough not to be AMO, certainly not a temperature profile driven by AMO.
So Where is Amo?
MY reply to Dikran's post 57 can be found here.
http://www.skepticalscience.com/news.php?p=3&t=123&&n=1975
So where is Amo? Perhaps we should look where he was last reported being seen.
The first graph plots 5-year rolling average of AMO (after Enfield) over the last 130 years along side the three surface global temperature records, all averaged, de-trended and re-based for comparison.
So is the wobble in the global temperature records actually AMO? Like 'Where's Waldo?' it isn't just any old kid with glasses in a colourful jumper & bobble hat that we are looking for.
Now these different temperature records do provide differerent breakdowns of the global total. NASA GISS, for instance, provides temperature records for different latitudes of the globe.
The graph below compares such data for different latitudes for the Southern Hemesphere against AMO. I see no sign of AMO there.
An identical graph but the Northern Hemesphere does show a goodly wobble. So can we see Amo in the Northern Hemisphere?
Perhaps. But here's a thing. The size of those wobbles increase as the Northern latitude increases and the size of the trend that has been subtracted to present the graph also increases with that same increasing latitude, as the fourth graph here illustrates.
So here's a question. If this increase with latitude applies to both wobble and trend, would this not indicate a common source for both of these elements of the global temperature record? If not, what mechanism would provide the same trend for different causes, one AMO-caused the other a global-wide climate forcing. This is a tricky question because according to the proposal before us, AMO does not cause any trend.
So Where is Amo?
The NOAA NCDC temperature data is broken into Land and Ocean as well as for different latitude zones (the zones differing from the GISS zones) so that might show us where he is.
The graph below shows the NCDC Global data in red (already shown in a post above but here more heavily smoothed to assist the presentation). So is the NCDC Global temperature wobble a signal from the AMO (shown in black)?
Looking at the Land and Ocean data which is also plotted, the answer is 'No, not unless Amo has a limp'. It would require explanation as to why the dip in AMO in 1910 made such a small impact on Land and big impact on Ocean SST and then in 1970 the dip made a big impact on Land and small impact on Ocean SST.
The best we can hope is that the red wobble is some big kid with a limp and Amo is hidden behind him. Look! Do I see there the bobble on the top of Amo's hat? Find out in the next thrilling installment of "Where's Amo?"
So Where is Amo?
The land of the southern hemisphere isn't a promising palce to look. It has only half the area of the land in the northern hemisphere, & over a quarter of it is Antarctica which temperature-wise has a mind of its own. But even so, can we see Amo there?
No sign of him on the Southern continents. (Then we could have expected that because the temperature data for the Southern hemisphere showed no sign of Amo. But you can't go turning over two pages at once in a children's book, can you?)
So is Amo up North on the continents, hiding behind that fat kid with a limp?
Well, the 'limpy' bit that bottoms out in 1970 drops far earlier than Amo but that isn't a problem because it isn't what were looking for - th1970 dip is the kid with the limp (that is unless Amo was on holiday for some reason in 1910). So it's the earlier bit that bottoms out in 1910 is where we should be looking.
60-90N - That doesn't really drop into the 1910 dip. It's sort of already there.
30-60N - That doesn't really drop into the 1910 dip at all but stays up until 1940.
0-30N - That does dip down to 1910 but sort of stays down from there all the way to 1970. If we decide the levelling off 1910-40 is the bobble on Amo's hat, then we'd be adding a contirbution to the peak-to-peak Global Amo wobble of 0.1C x 9% of global area = potentially 0.009C max. But can we identify it as Amo just from the bobble on his hat?