SkS Analogy 5 - Linear, Non-linear, and Coastal Flooding
Posted on 23 May 2017 by Evan
Tag Line
We age linearly and earn non-linearly.
In a warming world, coastal flooding occurs non-linearly … or faster!
Elevator Statement
Linear means a straight line, non-linear means a line that is not straight, and is often a simple, curved line. Consider the following examples from our everyday lives that illustrate linear and non-linear behavior.
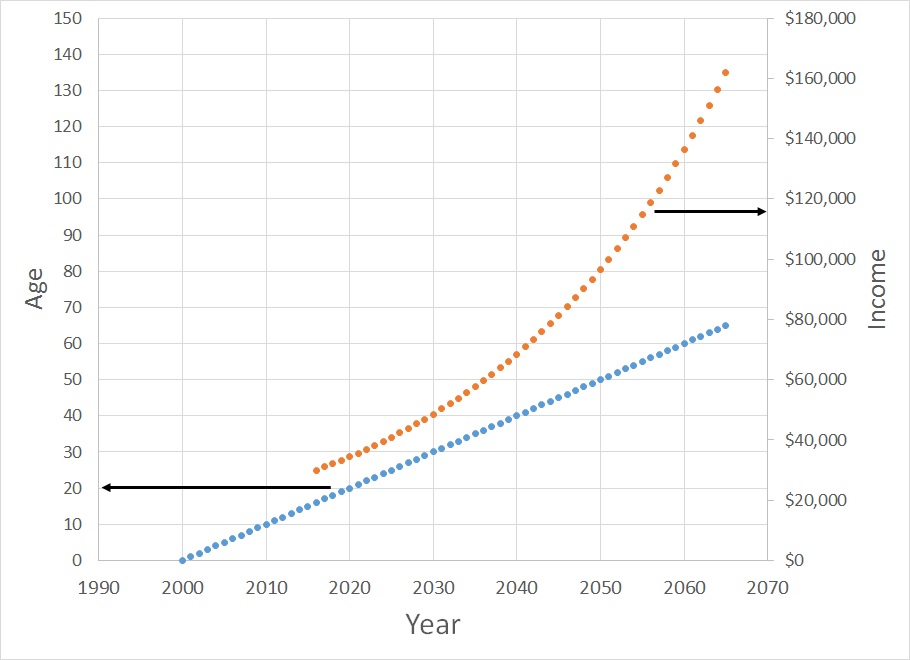
- Our age increases linearly, because our age increases at a constant rate, 1 year per year.
- Our income increases non-linearly, because our income increases at a varying rate, x% per year.
When the change of your salary is related to your salary, you get a non-linear response. To illustrate, suppose you got a 3.5% raise each year.
- Year 1: Start with a $30,000/year salary.
- Year 2: 3.5% more than $30,000. New salary is $30,000 + 0.035*30,000 = 31,050.
- Year 3: 3.5% more than $31,050. New salary is $31,050 + 0.035*31,050 = 32,137.
- ...
Suppose a person is born in the year 2000. If we do the simple thing and plot their age on the “Y” axis and the year on the “X” axis, we get a straight line, as follows. We call this a linear relationship. If they start working at age 16, for $30,000/year, and if they get a pay raise of 3.5%/year until they retire at age 65, then we get the non-linear growth of income.
Climate Science
Researchers like James Hansen regularly talk about the doubling time for ice melt, especially in his recent paper “Ice melt, sea level rise and superstorms: evidence from paleoclimate data, climate modeling, and modern observations that 2°C warming could be dangerous,” published by Hansen and 18 co-authors. What do they mean when they say “doubling time?” In their paper they talk about 10-, 20-, or 40-year doubling times that could yield multi-meter sea level rise in 50, 100, or 200 years. What does all of this mean? In a nut-shell, doubling times are techno-speak for non-linear relationships. We can break down doubling times in terms of annual percentage increases as follows, similar to the annual 3.5% salary increase of our young worker.
| Annual Increase [%] | Doubling Time [years] |
| 1.8 | 40 |
| 2.3 | 30 (within the IPCC 5th-assessment projections) |
| 3.5 | 20 |
| 5.0 | 14 |
| 7.0 | 10 |
Let’s work out what all of this means for our young worker who has their first job, and in the not too distant future may be considering buying property on the East Coast of the USA.
Sea level is currently rising at about 3 mm/year. Starting with this rate, we work out how fast sea level rises for the following annual rates of increase: 0, 2.3, 3.5, 5.0, and 7.0%. Note that a 0% annual increase implies a linear rate of increase of sea level: sea level will be assumed to rise at a constant rate of 3 mm/yr into the future. The non-zero rates imply non-linear rates of increase as shown in the following plot.
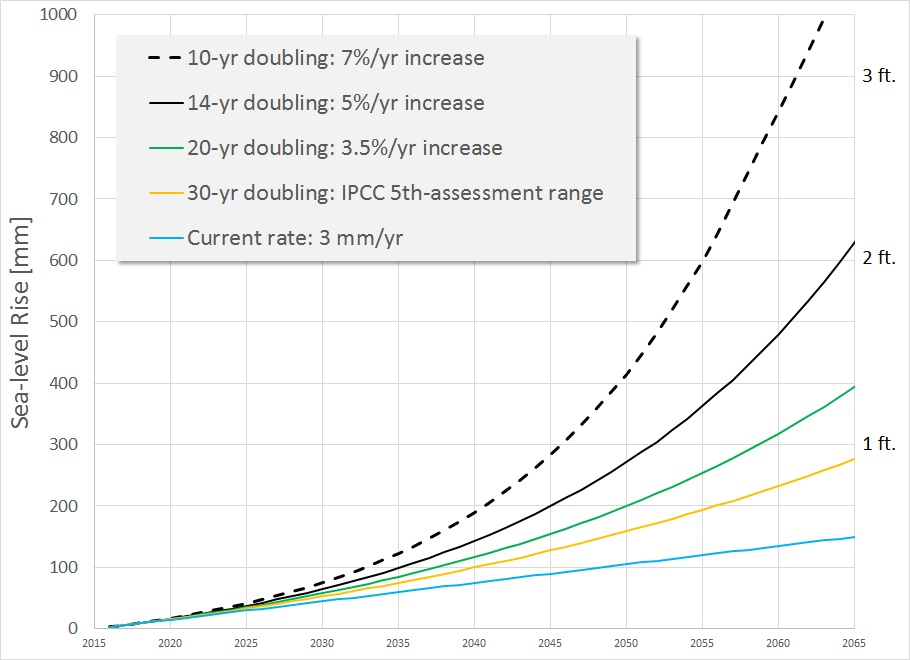
Note that making sea-level predictions is much more complicated that using this simple plot, because sea-level responds not only to melting ice, but also to the warming oceans (causing the water to expand, much like in an old-fashioned mercury thermometer) and to local changes in land elevation due to other natural processes. What this plot allows one to do, however, is to convert from techno-speak of ??-year doubling times to what that means in terms of sea-level rise over a specific time period.
So what does all of this mean for someone who buys a house near the East Coast of the USA, and is concerned about the future of their property? Because some East-coast states have been reluctant to embrace even the conservative IPCC forecasts, much less the more current results from researchers like James Hansen and others, our coastal homeowner to-be does their own research and uses the above plot to determine a “safe” place to buy a house, consistent with their risk tolerance. The 14-year doubling time is included because Hansen et al. note that “Recent ice melt doubling times are near the lower end of the 10-40 year range”, and a 14-year doubling time works out to an annual rate of increase of 5%, which is a nice, round number. So whereas 10-yr. doubling times can be viewed as a worst-case scenario, the 14-yr. doubling time is one for which there is some basis from current observations, although the data set from which Hansen et al. draw their conclusions is too short to be definitive. However, considering that we buy insurance to cover improbable events, when current research suggests a probable event such as coastal flooding, it is only prudent to plan accordingly. The scenario we accept from this graph depends on how averse we are to risk. Perhaps the important question to ask is not what risk scenarios our individual home owners are selecting for themselves, but rather, what risk scenarios are East-coast legislators imposing on their constituents?
Because coastal real-estate is valuable, by definition, near the coast we develop every scrap of land possible, meaning that any amount of sea-level rise will affect someone: there is no such thing as inconsequential sea-level rise. It is just a question of how rapidly we will flood coastal property, how many people will be affected and at what rate, and how fast the cost will rise for tax payers who subsidize government-backed flood insurance.
On top of these smooth processes there may also be lurking hard-to-predict, abrupt events. If you have ever seen an unbroken icicle sitting in a snow-bank in front of your house, you have clear evidence that glacier calving from the roof of your house does not always occur predictably and slowly: at some point melting icicles break off and fall. Sometimes ice sheets let lose all at once, causing a sudden increase in ice flow. Such scenarios are not included in IPCC forecasts because they are difficult to predict. But there is plenty of evidence from the paleo record of rapid accelerations of ice loss … at a time when the climate was being forced only a fraction as fast as we are pushing it today.
The good news is that future sea-level rise will make the cheap property sitting back from the coast much more valuable, beach-front property.































 Arguments
Arguments






























A better example of exponential growth would have been body weight from conception to puberty, set off against age. Salaries rise mostly with inflation, and are not a real example of growth. There are lots of good explanations of exponential growth floating around. Defining 0% growth as 3mm/annum does not seem to me very good practice. Discussions around GDP growth also exhibit tendency, to talk about 0% GDP when they mean %0 growth, or even worse, decreasing GDP when they mean the second order derivative is decreasing down from 2.5% to 1.7%.
Note also that thermal water expansion is (almost) linear for the relevant temperature ranges.
Omitted from the complicating sea-level effects: stronger (c.q. weaker) currents; stronger tidal action (more water); gravity (less ice mass pulls water elsewhere); crustal rebounding (displacing water).
By the way, in the ancient world (Babylonia, Sumer) they also expressed interest and exponential growth in terms of doubling time. Most agricultural debts were annulled after the first doubling, regardless of how much principle remained. Doubling time is actually a more natural way to think, because it also gives an intuitive grasp of the limits to infinite doubling, the magic of compound interest, etc.
Thank you for the comments JWR. Your points are well taken. These analogies will be evolving as we get feedback, so when I rework this I will consider your input. I also understand that the sea-level analysis is overly simplistic.
That said, I still maintain that salaries exhibit the effect I was looking for: the increase is proportional to the thing itself, whether the driving force is inflation, promotion, or something else. By contrast, aging is a constant for everytone. This basic differentiation is likely new to many people. You are obviously very well educated on these matters, but the main goal of the analogies is to introduce scientific concepts to the lay person.
Thanks for your input and suggestions.
Humanity is used to stable and slow rates of sea level rise, and I think we undersetimate the problems of accelerating sea level rise, and humanity is in for a rude multi generational shock.
Consider for the past couple of centuries, sea level rise has been pretty slow around 100 - 200 mm century, until later last century anyway. In my city buildings have been designed with this slow trend in mind, and its been assumed it would be a roughly linear trend, and also on the basis of general storm flooding in mind, with certain floor levels above ground level, and a building life of somewhere from 50-80 years. By the time sea level has risen significantly by 180 mm over a century or so, buildings have been protected by their floor levels, and reached the end of their natural lives, in the vast majority of cases.
Flood frequencies have also been predicatable and constant over time.The slow rate of change in sea level and flood events has made planning predictable, and problems have been generally limited. Floods are of course terrible, but have generally been one big one per 100 years and now this is all changing.
This has all now changed with the understanding sea level rise is going to accelerate. It is of course already changing in places like Florida which are low lying and experiencing significant accelerating sea level rise combined with flood events etc. With 500mm sea level rise by end of this century plenty of buildings will need to be replaced before they reach the end of their natural lives. With 1000 mm the problem increases.
Increasing numbers of floods due to other facets of climate change adds to this problem and also interacts with sea level rise itself making things worse. Florida and Miami in particular are good examples.
But that is just the first stage of sea level rise, affecting existing buildings this century. New buildings will then presumably be planned with some sort of accelerating sea level rise trend in mind. I thought we were looking at a quadratic sort of curve as opposed to exponential, by the way, but the analogy of compound interest is still a good.
But nobody is sure exactly what the longer term rate of sea level change will be, so how high do you design buildings above ground level? This is not so easy to say, and will have to be based on a guess at the most likely trend over the life of the building probably the middle IPCC estimates. It will lead to complex planning zones with certain requirements.
But its not just buildings as you have to plan roads and drains and drains generally have longer lives than buildings and stop functioning when water levels rise. So it gets hard to work out how to plan.
And how far inland do communities retreat to in an uncertain changing sea level rise scenario? My government has already ruled out governments building barriers, so it's a question of organised retreat, apparently. Again it will require an assessment of building life, and infrastructure life against a guesstimate at the most likely rate of sea level rise (probably taking the middle scenario). And who is going to want to calculate and enforce all this? It will be politically contentions, and full of mistaken judgements. The process could go on for centuries, in some sort of staged retreat one part of a city at a time gradually hopping inland, or alternatively building barriers that themselves will not last forever.
And do cities plan for sea level rise a century ahead leading to a multiple staged retreat, or do they look at several centuries and put larger areas of land off limits?
It will dislocate and cost communities physically, economically, and will have all sorts of socio- economic implications as land prices collapse, and people loose major assets. Nobody is going to want to buy low lying properties, or insure against sea level rise, and governments (tax payers) will as usual end up bailing people out. I think they will have to. It will however become politically contentious, and a drain on government resources for many centuries.
Thank you Nigel for your observations and writing about your own experiences.
I thought we were looking at a quadratic sort of curve as opposed to exponential...
The original point of this analogy was to educate people about the difference between linear and non-linear trends. For many readers of SkS this is obvious, but is likely a new concept to non-technical readers. I simply chose sea-level rise to illustrate this, so that when they read/hear/see the concept of non-linear being used elsewhere, they have some familiarity with how it differs from linear. The analogy morphed into what it is, but I was not intentending to to write an authoritative essay on expected sea-level rise.
"I thought we were looking at a quadratic sort of curve as opposed to exponential..."
With a noisy data set like sea level, which shows short term (a few years) ups and downs due to various factors, it can even be hard to tell whether the change is linear or not. Telling the difference between exponential or quadratic would be even more difficult!
We could go all mathy and talk about first and second derivatives, etc., but that would detract from Evan's simple analogy. If the reader really wants to get into this more seriously, then I suggest they wander over to Tamino's where he has some good posts on sea level rise, including this one on acceleration.
Evan @4, I understand your point. Your article was basically just explaining linear versus accelerating / exponenential/ curvilinear using various analogies. It made some good points.
Here's a very simple analogy. The car washing analogy. Turn the tap on and leave it and you have a linear water flow. My car was really dirty last week, and I found myself turing the tap up, and up over time, which is an accelerating water flow over time. Sea level will be a smoother acceleration than this, but maybe also a bit jerky at times.
I just recall that this website had a graph of sea level rise over the last 150 years which had a curve fitted that looked like a quadratic or was described as a quadratic, and sea level forward projections until 2100 for my country are a quadratic. We have been arguing about this projection recently, as to how valid it would be. I'm not even really a maths person, but when reading the article those things were on my mind. But yes, it's a bit beside the point of the article.
Um, it's "icicle". Please fix. No spell-checker will fault "ice-cycle" unfortunately.
Thanks for finding and pointing out this typo. Fixed.
The last sentence is is a winner in this article, Evan. It encompasses the punishment for those greedy developers, who would like to cash out of waterfront property values and who deny AGW precisely for that reason.
In that respect, I only regret that SLR does not progress fast enough (or in a big burst similar to a biblical Yahweh punishment) but unfortunately, SLR is a problem developping in more than one generation timeframe, so our children are about to receive most of the ensuing mess.
Geometric series model applied to the real world always has the flaw that it does not consider the limitted amount of resources to draw the series. E.g.: consider repetitively folding a 0.1mm thick piece of paper as many times as you can. How "thick" does your piece becomes when you fold it, say 50 times (in theory of course)? Answer: from the Earth to the Moon. An obviously absurd outcome, because a simple model of geometric time series representing the process of parer folding did not consider the very limitted physical resources (a piece of paper).
In case of melting ice sheets, the resources are large but limitted to 70m of SLR-equiv. And when we're talking about an SLR of "many meters" we already are within said limit. We can approximate the current icesheet melting rate with geometric series doubling every 10 or so years (as we do here and as Jim does in Hansen 2016) when dSLR is few mm/y. But our model cannot be accurate at dSLR much higher. Not Jim nor any other researchers, estimated at what dSLR the inflexion point is when such model becomes inaccurate (overestimating) and SLR must slow down, then definitely stop at ca70m.
My favorite meme on this subject, based on the words of the late Professor Al Bartlett:
http://ocean.si.edu/sea-level-rise
Based on the data in the aforementioned article, the rate of increase in the rate of sea level rise was appox .0036 per annum (0.36% ) from 1900 to 1990. The rate of the increase in the sea level rise from 1990 to 2000 was approx .061 per annum (6.1%). The rate from 2000 to 2016 reverted back to .0040 (0.4%). which is much closer to the historical norm.
The large rate of increase from 1990 to 2000 would seem to be connected to the change in method of measurement. Other than the anamoly for the short ten year period, it would seem very unlikely that the rate of increase will suddenly shift upward from less than 1% per year upwards of 6-10% as speculated in the article or even the 2.3% projected by the IPCC in their 5th assessment.
Thanks for the reference Joe and for your comments.
It is likely dangerous to rely too much on historical trends. We know that we are warming the planet faster than at any time in the known paleo record, and we also know that ice melts as it warms. We also know from measurements that the melt from Greenland and Antarctica are speeding up, and this is why doubling times for galcier melt is used to estimate future sea level rise. Even if there was an anomaly in the 1990's or even if there was a change in measurement method, it does not change the basic math that there is over 200' of sea-level rise in ice worldwide, and that the rate of ice melt increases as Earth warms. The only real question is how fast the rate of sea-level rise will increase (i.e., what will be the doubling time). There is likely nothing in the records for the last 100 years that can be used to make good projections into the future, because up to now the big glaciers have contributed little: sea-level rise has so far been controlled mostly by thermal expansion.
Based on the math, the rate of increase has been fairly constant. (other than the anomoly during the 1990-2000 time frame which is pointed out in the article - though you have to actually run the math to notice). That rate of increase in the rate of sea level rise has been in the 0.3-0.4% range which is a far cry from the IPCC estimate of 2.3%
It is worth pointing out that the curve for warming vs Atmospheric Carbon dioxide is downward curving. The climate sensitivity theory says that for each doubling of CO2 we have a temperature increase of, say, 3.5 degrees C. So if we go from 200 to 400ppm this increases the temperature by 3.5 degrees but we have to go from 400 to 800 to get the next 3.5 degree rise. Of course, this ignores tipping points such as what happens when the Arctic is mostly ice free for a significant part of the summer.
Joe: The research described in this article suggests that your computations and conclusions are dated...
A new scientific analysis finds that the Earth’s oceans are rising nearly three times as rapidly as they were throughout most of the 20th century, one of the strongest indications yet that a much feared trend of not just sea level rise, but its acceleration, is now underway.
“We have a much stronger acceleration in sea level rise than formerly thought,” said Sönke Dangendorf, a researcher with the University of Siegen in Germany who led the study along with scientists at institutions in Spain, France, Norway and the Netherlands.
Their paper, just out in the Proceedings of the National Academy of Sciences, isn’t the first to find that the rate of rising seas is itself increasing — but it finds a bigger rate of increase than in past studies. The new paper concludes that before 1990, oceans were rising at about 1.1 millimeters per year, or just 0.43 inches per decade. From 1993 through 2012, though, it finds that they rose at 3.1 millimeters per year, or 1.22 inches per decade.
Scientists say the pace of sea level rise has nearly tripled since 1990 by Chris Mooney, Energy & Environment, Washington Post, May 22, 2017
William - CO2 forcing goes up with the log of the concentration, but since CO2 are actually increasing faster than exponentially the forcing is rising faster than linearly.
Taking the Keeling CO2 data yearly averages and running the log of them gives the forcing curve (easy to do in Excel). A linear forcing would show as a straight line, but the log data shows a rising curve, demonstrating that CO2 is increasing more than exponentially.
Joe @14, "That rate of increase in the rate of sea level rise has been in the 0.3-0.4% range which is a far cry from the IPCC estimate of 2.3%"
Yes but so what? Some past rate of change does not have to continue forever. The IPCC look at physical processes going forwards. For one example, they are confident positive feedbacks etc will increase the rate of ice melt especially around mid century so they think things will accelerate.
The following is a graph of sea level rise for NZ, over the past century and combined with standard IPCC predictions going forwards. The transition from past trends to the predicted larger acceleration is reasonably smooth, so entirely plausible.
Hey joe @12.
I think your calculations of SLR acceleration need some explanation here. An annual 0.35% increase in the rate of SLR would result in a doubling in the rate every 200 years. With 1900 SLR not much greater than 1mm/yr, how is it we see already SLR well above 3mm/yr, a trebling after a single century (and that before adjustment for terrestrial storeage and aquifer depletion which is calculated to have reduced SLR)? While you do also calculate higher values in recent decades (the 0.61% increase for the 1990s and the 0.4% since 2000), these do not even start to explain all the SLR being measured today.
I am going to refer you back to the the citation from the smithstonian. The rate of growth was straight from the data provided which is also from NOAA. The anomoly in the data was from 1990 to 2000 which had the 6.1% growth in the rate of increase. Using the NOAA data and the data from the citation, the rate of increase after 2000 reverts back to the norm of 0.4%.
MA Rodgers - Following up on your comment - It appears from the follow up comments that you were the only one who attempted to check the math which I appreciate. (simple excel calculation) and yes, 0.36% is a doubling in approx 200 years. (or approx 192 years) Again I appreciate someone actually reviewing the math.
The historical norm has been a rate of 0.36% to 0.4% increase for the SLR. When I plugged the numbers into the spreadsheet for each year since 1870, virtually each year agrees with the data from NOAA. With the exception of the years 1990-2000 when the rate of increase jumped for those ten years to 6.1%. Which then reverted back to 0.4% annual increase.
With regard to J Hartz comment, The data is through 2015. The study John cites is from data through early 2016 (published 2017). I doubt the rate of increase jumped that significantly in 18 months. Further The actual study is behind a paywall, though based on the data from NOAA, the headline from the WP is more than a little misleading. The largest increase in the rate of sea level rise occurred during the change in the method of measurement. (I will add that I have not had the time to confirm if the large increase was due to the change in the methodology of measurement, only that all other years were well within the historical norm.
Joe:
In your citation in the Smithsonian it says:
"Today, global sea level is 5-8 inches (13-20 cm) higher on average than it was in 1900. Between 1900 and 2000, global sea level rose between 0.05 inches (1.2 millimeters) and 0.07 inches (1.7 millimeters) per year on average. In the 1990s, that rate jumped to around 3.2 millimeters per year. In 2016 the rate was estimated to be 3.7 millimeters per year, and it is expected to jump higher by the end of the century."
I think this quotation contradicts your claims. Please quote from the paper to support your claims. It appears to me that you have misread your source of data.
This blog from Tamino analyzes the recent sea level rise. Here is a key graph:
This graph clearly shows that sea level rise has not decelerated since 2000. Tamino claims that the rise is accelerating. His graph shows a rate of approximately 3.0 mm/yr in 2000 increasing to 3.5 mm/yr in 2015. There is a wide error bar but the rate cannot be claimed to be decreasing.
That quote is consistent with my statement and the math. The Smithstonian artcle, the Church white chart is likewise consistent.
A change from 3.0 in 2000 to 3.5 in 2015 is 1.03% (based on the Tamino) vs the 6.1% rate from 1990 to 2000. This difference of 1.03% from Tamino's data and the 0.4% based on the smithstonian/NOAA data is well within the error bar.
It should be noted that everal comments later and only one person has crossed checked the math.
After adjusting from
Hey joe @21.
I find it strange you do not see the problem. I say 0.35%/yr doubles in 200 years. You say 0.36% doubles in 192 years, essentially the same finding. And you insist "The historical norm has been a rate of 0.36% to 0.4% increase for the SLR."
Yet the SLR data over the last century or so (a significantly shorter period) shows far more than a doubling in the rate of SLR.
Now we can add to these contradictory positions that you occupy because you tell us that when you "plugged the numbers into the spreadsheet for each year since 1870, virtually each year agrees with the data from NOAA." Yet when I set your values for SLR increase (1880-1990 0.35%/yr, 1991-2000 0.61%/yr, 2001-2013 0.4%/yr) into a spreadsheet alongside Church & White data (1880 to 2013), the inter-annual SLR variations prevent any checks on an annual basis and the longer-term accelerations in SLR do not match your values, virtually or otherwise.
Joe,
I did not realize that you were estimating the change in acceleration. Tamino's graph may be leveling out but the error bars are wide. The smooth used is more error prone at the ends. We will know more in 5 years.
I would like to withdraw from this conversation to prevent dog piling.
Michael, Joe, et al:
I think there has been some cross-talk. Joe's use of the phrase "rate of increase" can be hard to follow.
and
...do have rather different meanings, as "the rate" already talks about an increase. So "the rate has increased" means that the new rate is higher than the old rate.
To delve into what a former student of mine once called "all that math $#!^":
I think Joe has used the second meaning, and Michael admits to having been thinking the first.
...unless Joe really means "change in acceleration" as Michael says above, which is the rate at which the change in rate has been changing... or the third derivative. (Yes, I am being obtuse on purpose.)
So, can people try to be a bit clearer with the terms they use, please? I suggest:
...Boy, its hard to work a simple analogy without getting into the weeds, isn't it?
Oh, and Michael's link in #22 is the same Tamino post I linked to in #5....
Joe, using Church and White (2011) (data downloadable here) as a basis of discussion, they claim that:
0.009/1.7 =0.0053, or 0.53% increase per annum in the rate of sea level rise (2nd derivative) over the course of the 20th century. More importantly, that rate of increase extended over the period 1900-2009 would result in a rate of increase of sea level (first derivative) 2.27 mm/year in 2009. The actual rate of increase of sea level for the decade terminating in 2009 was 3.41 mm per annum. What is more, by 2014, the rate of increase for the preceding decade had risen to 4.53 mm/yr. There is a relatively smooth rise in rate of sea level rise over a decade from 2000 to 2014 of 0.17 mm/yr^2, which is approximately a rate of increase in the rate of increase of sea level of 5% per annum.
This raises two questions:
Given that your estimates of the rate of increase of the rate of increase of sea level are under estimates whether we take the 20th century values, or the more recent much more rapid rate of increase, where did you get those estimates from (or how did you make them)?
Given that the rapid rate of increase in sea level rise coincides with the onset of rapid loss of ice from the Greenland and West Antarctic Ice Sheets, is there any reason we should not expect it to continue, and therefore project a 14 year doubling time of the rate of sea level rise over at least the first half of the 21st century?
We all need to keep in mind that Sea Level Rise does not occur uniformily throughout the global ocean system. Cases in point...
A 2016 Rutgers study found that seas near New Jersey could rise between 1 and 1.8 feet by the middle of this century under a scenario of low carbon emissions. But under a high emissions scenario, seas could swell as high as 4.5 feet by 2100. Recently, a National Oceanic and Atmospheric Administration study estimated mean global sea levels could rise as high as 8 feet by the end of the century.
Another study by researchers at the real estate firm Zillow found that nearly two million U.S.homes worth almost $900 billion could be underwater by 2100. The researchers weren’t referring to a situation where the market value of a home dips below the value of the mortgage; they literally meant underwater, swamped by rising sea levels.
Zillow researchers looked at coastal states where sea levels would rise by six feet by 2100. In Florida, the most vulnerable and heavily developed, they found nearly 1 million homes – one of every eight in the state – would be underwater. The next most vulnerable state was New Jersey, where 190,429 houses would be inundated.
How Rising Seas and Coastal Storms Drowned the U.S. Flood Insurance Program by Gibert M Gaul, Yale Environment 360, May 23, 2017
Tom Curtis @28,
Concerning your first question posed, I suspect that the values presented thus by joe@12 :-
- were calculated from the rates of SLR described in the second pragraph of the Smithsonian Ocean ortal SLR page linked @12:-
(Note the 3.4mm/yr 2016 figure is also given as 3.7mm/yr further down the Smithsonian article.) If this Smithsonian quote is interpreted as stating that the SLR 1900 was 1.2mm/yr, 1990 1.7mm/yr, 2000 3.2mm/yr and 2016 3.4mm/yr and an average percentage for the acceleration of SLR then calculated, you obtain 1900-1990 - 0.35%/yr (assuming a full century and not 90 years), 1900-2000 - 0.71% over 10 years, 2000-16 - 0.4% over 15 years. This is a bit of a stretch but is not a million miles from the values presented @12.
The "NOAA" data mentioned @21 (and also "smithstonian/NOAA data" @23) I suspect is the Church & White data you suggest @28. A plot of the exponential increase using the 'joe' values will slice through the wobbles of the Church & White data up to the 1990s. However, it is evident that the 'up' wobbles are larger than the 'down' wobbles which is why the 20th Century SLR is greatly underestimated by the assumed exponential growth.
MA Rodger @30, comparison of the Smithsonian's claims to both Church and White (2011) and Jevrejeva et al (2014) data suggests the Smithsonian is basing its claims on Church and White for the interval preceding the satellite data, and the satellite data thereafter. That conclusion is given circumstantial support by the fact that one of the author's, Joshua Willis, works for NASA, whose vital signs page uses just that combination of data.
In any event, I interpret the Smithsonian quote as saying, not that sea level rose at a rate of 1.2 millimeters per year in 1900 and 1.7 millimeters per year in 1990, but that the linear trend from 1900-1990, given uncertaintly, lies between 1.2 and 1.7 millimeters a year. In support of that, using the linest function on the Church and White data from 1900-1990 yields a linear trend of 1.5 +/- 0.3 mm/year. I would conclude that no estimate of acceleration from 1900-1990 can be made from the Smithsonian statement, and certainly not one in contradiction of Church and White itself.
Nor can the difference between the 1.7 mm/year upper bound on the uncertainty interval fo the 1900-1990 trend be used to calculate a rate of acceleration from 1990-2000. That is especially the case given that the second part of the Smithsonian statement appears to be based on the satellite data, and therefore is not directly comparable.
For what it is worth, the linest estimated OLS trend for 1991-2000 is 2.16 +/- 0.4 mm/year. From 2000-2014 it is 4.0 +/-0.2 mm/year. Again, that shows a noticable acceleration.
Of course, Joe may have been relying on a different data source, in which case this analysis is irrelevant to his claims.
(Note: all calculated error margins given for 1 standard error.)
Tom Curtis @31,
I agree that the interpretation of the Smithsonian quote I present @30 is ludicrous and should be interpreted as you set out. Yet the interpretation @30 does after a fashion yield the values presented by joe@12. Despite being shown the need for a proper explanation, joe says no more than "I am going to refer you back to the the citation from the smithstonian. The rate of growth was straight from the data provided which is also from NOAA."Of course there is nothing preventing joe properly explaining how he derived his values if my explanation of it is wrong.
Tom Curtis @31, thanks for making sense of this mystery. It appears to me Joe had the right method, but the wrong assumption on data previous to 1990, which is maybe understandable, as it wasn't so clear.
This graph is based on Church and White with the satellite data stiched on, from 1880 to 2016.
I can't see any increase in the "rate of the rate" from 1900 - 1990. It looks flat overall, but has a convex hump. There's an obvious increase in the rate of the rate from 1990 onwards.
nigelj @33, if you mean one of the graphs from this page by Tamino, then the Church and White data is actually from 1800-2009 (ie, the original data from the paper without updating), or from 1930 for the last three graphs. Of the graphs there, this one seems to best fit your description:
You will notice that though the data is noisy, the slope of the smoothed curve over the initial decades is less than that over the final decades, a fact that indicates acceleration.
Better yet is this graph, which determines acceleration on the assumption of a parabolic fit from each date up to 1990, showing uncertainty intervals:
The initial and 1900 values plus uncertainty intervals are close to those stated by Church and White, suggesting that is the technique they used. Tamino goes on to use better techniques to understand the structure of the acceleration, but only with the data from 1930.
For what it is worth, using a linear fit on the annual differences in sea level, the OLS trend is 0.006 +/- 0.019 mm/yr2. That is, it shows acceleration, but it is not statistically significant. For comparison, using the same technique on the data to 2009 shows an OLS trend of 0.018 +/- 0.016 mm/yr2; while from 1900 to 2014 shows an OLS trend of 0.019 +/- 0.015 mm/yr2. All errors are for 1 standard error only, so none of the accelerations shown are statistically significant, though all are greater than that reported by Church and White. Because of the accelerations shown, it is more likely than not that using the better techniques used by Church and White, and by Tamino in his last figure, would also show acceleration over that interval. Because of the larger relative errors, that is not certain, and it is certainly not clear that the data to 1990 would show a statistically significant acceleration, even using those better techniques.
Tom Curtis @34, thanks for the explanation. I meant this sea level rise graph, which is very similar to your first example anyway, but with some trend lines shown and extended from 1880 to about 2016. I could not reconcile this with what Joe was claiming until I read your explanation.
I copied and pasted the wrong thing somehow above, hopefully it works this time. I have a new laptop, so I'm going to blame that.
Recommended supplemental reading:
10 things you should know about sea level rise and how bad it could be by Rob Motta, James White & R. Steven Nerem, Capital Weather Gang, Washington Post, May 20, 2016
nigelj, that graphic is through 2012. This one is updated through 2015:
Bigger image here.
Daniel Bailey @37, ok thanks.
But one thing mystifies me. I would have expected sea level rise since 1900 to have accelerated in a roughly smooth curve, but squinting my eyes down the increase does look to be in a series of steps, for example after 1930, there is a definite and quite abrupt change in pace, and again after 1990 you have the same. Or maybe the lines imposed on the graph make it look that way.
But if it is a series of step changes, especially after 1990, why would that be? Did something happen around 1990 in terms of ice sheet behaviour, to cause this? Did melting in the arctic region accelerate about then?
nigelj @38
Without wading through all the comments, I remember reading somewhere that initially the contributions to sea-level rise were mainly from glaciers and thermal expansion. Recently, however, meltwater from the Greenland and Antarctic ice caps has become a third important source. This apparently explains the recent acceleration. If I've misunderstood, somebody please correct me.