A Cloudy Outlook for Low Climate Sensitivity
Posted on 5 December 2010 by dana1981
One of the largest uncertainties in global climate models (GCMs) is the response of clouds in a warming world. Determining which types of cloud cover will increase or decrease, whether that will result in a net positive or negative feedback, and how large the feedback will be, are major challenges. The variation in global climate sensitivity among GCMs is largely attributable to differences in cloud feedbacks, and feedbacks of low-level clouds in particular.
For climate scientists who are skeptical that anthropogenic greenhouse gas emissions will cause a dangerous amount of warming, such as Richard Lindzen and Roy Spencer, their skepticism hinges mainly on this cloud cover uncertainty. They tend to believe that as the planet warms, low-level cloud cover will increase, thus increasing planetary albedo (overall reflectiveness of the Earth), offsetting the increased greenhouse effect and preventing a dangerous level of global warming from occurring.
Recently some studies have examined the cloud feedback specifically in the eastern Pacific region. Stowasser et al. (2006) found that:
"In terms of the sensitivity of the global-mean surface temperature, almost all the differences among the models could be attributed to differences in the shortwave cloud feedbacks in the tropical and subtropical regions."
In order to evaluate this uncertainty, Lauer et al. (2010) used 16 GCMs and the International Pacific Research Center (IPRC) Regional Atmospheric Model (iRAM) described in Lauer et al. (2009) to simulate clouds and cloud–climate feedbacks in the tropical and subtropical eastern Pacific region. To investigate cloud–climate feedbacks in iRAM, the authors ran several global warming scenarios with boundary conditions appropriate for late twenty-first-century conditions (specifically, warming signals based on IPCC AR4 SRES A1B simulations).
Figure 1 shows the results of the 16 GCMs, iRAM (bottom center), and satellite observations (bottom right). A clearer version of this figure can be seen in Figure 1 on Page 6 of Lauer et al. (2010).
"The authors find that the simulation of the present-day mean cloud climatology for this region in the GCMs is very poor and that the cloud–climate feedbacks vary widely among the GCMs. By contrast, iRAM simulates mean clouds and interannual cloud variations that are quite similar to those observed in this region."
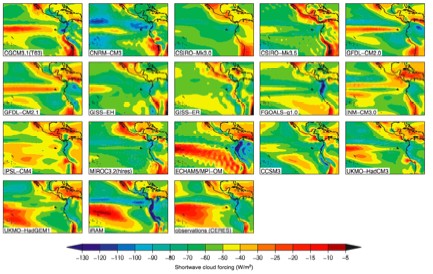
Figure 1: Annual average TOA shortwave cloud forcing for present-day conditions from 16 IPCC AR4 models and iRAM (bottom center) compared with CERES satellite observations (bottom right)
Thus the study shows that that iRAM simulates recently observed cloud cover changes in this the eastern Pacific more accurately than the GCMs, and iRAM also successfully simulates the main features of the observed interannual variation of clouds in this region, including the evolution of the clouds through the El Niño Southern Oscillation (ENSO) cycle. Given these conclusions, the logical assumption is that iRAM will also model future cloud cover changes more accurately. Operating under this assumption, the authors conclude as follows.
"All the global warming cases simulated with iRAM show a distinct reduction in low-level cloud amount, particularly in the stratocumulus regime, resulting in positive local feedback parameters in these regions in the range of 4–7 W m-2 K-1....The GCM feedbacks vary from -1.0 to +1.3 W m-2 K-1, which are all less than the +1.8 to +1.9 W m-2 K-1 obtained in the comparable iRAM simulations. The iRAM results by themselves cannot be connected definitively to global climate feedbacks, but we have shown that among the GCMs the cloud feedbacks averaged over 30°S–30°N and the equilibrium global climate sensitivity are both correlated strongly with the east Pacific cloud feedback. To the extent that iRAM results for cloud feedbacks in the east Pacific are credible, they provide support for the high end of current estimates of global climate sensitivity."
Lauer et al. (2010) is not alone in its conclusion that the low-level cloud cover feedback will be positive. Other studies analyzing satellite data from the International Satellite Cloud Climatology Project (ISCCP), the Advanced Very High Resolution Radiometer (AVHRR), and the Clouds and the Earth’s Radiant Energy System (CERES) such as Chang and Coakley (2007) and Eitzen et al. (2008) have indicated that cloud optical depth of low marine clouds might be expected to decrease with increasing temperature. This suggests a positive shortwave cloud–climate feedback for marine stratocumulus decks.
In another recent paper, Clement et al. (2009) analyzed several decades of ship-based observations of cloud cover along with more recent satellite observations, with a focus on the northeastern Pacific. They found that there is a negative correlation between cloud cover and sea surface temperature apparent on a long time scale—again suggesting a positive cloud-climate feedback in this region.
In short, while much more research of the cloud-climate feedback is needed, the evidence is stacking up against those who argue that climate sensitivity is low due to a strongly negative cloud feedback.































 Arguments
Arguments























 0
0  0
0 But with what we know of the radiative forcing of CO2 and its status as the Chief Control Knob of Temperatures, consider this graph carefully:
But with what we know of the radiative forcing of CO2 and its status as the Chief Control Knob of Temperatures, consider this graph carefully:
 At some point we may have to update the top graph with an arrow with this legend: Let the good times roll...
The Yooper
At some point we may have to update the top graph with an arrow with this legend: Let the good times roll...
The Yooper







Comments