CO2 emissions change our atmosphere for centuries
What the science says...
Individual carbon dioxide molecules have a short life time of around 5 years in the atmosphere. However, when they leave the atmosphere, they're simply swapping places with carbon dioxide in the ocean. The final amount of extra CO2 that remains in the atmosphere stays there on a time scale of centuries.
CO2 has a short residence time
"[T]he overwhelming majority of peer-reviewed studies [find] that CO2 in the atmosphere remained there a short time." (Lawrence Solomon)
The claim goes like this:
(A) Predictions for the Global Warming Potential (GWP) by the IPCC express the warming effect CO2 has over several time scales; 20, 100 and 500 years.
(B) But CO2 has only a 5 year life time in the atmosphere.
(C) Therefore CO2 cannot cause the long term warming predicted by the IPCC.
This claim is false. (A) is true. (B) is also true. But B is irrelevant and misleading so it does not follow that C is therefore true.
The claim hinges on what life time means. To understand this, we have to first understand what a box model is: In an environmental context, systems are often described by simplified box models. A simple example (from school days) of the water cycle would have just 3 boxes: clouds, rivers, and the ocean.
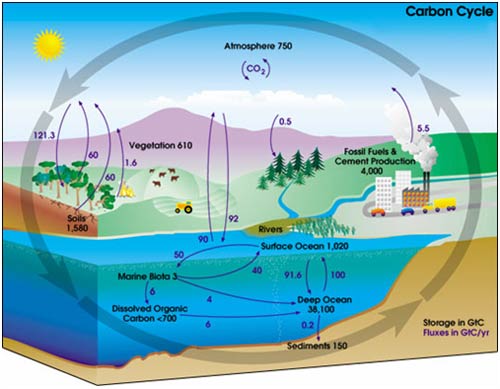
A representation of the carbon cycle (ignore the numbers for now) would look like this one from NASA.
In the IPCC 4th Assessment Report glossary, "lifetime" has several related meanings. The most relevant one is:
“Turnover time (T) (also called global atmospheric lifetime) is the ratio of the mass M of a reservoir (e.g., a gaseous compound in the atmosphere) and the total rate of removal S from the reservoir: T = M / S. For each removal process, separate turnover times can be defined. In soil carbon biology, this is referred to as Mean Residence Time.”
In other words, life time is the average time an individual particle spends in a given box. It is calculated as the size of box (reservoir) divided by the overall rate of flow into (or out of) a box. The IPCC Third Assessment Report 4.1.4 gives more details.
In the carbon cycle diagram above, there are two sets of numbers. The black numbers are the size, in gigatonnes of carbon (GtC), of the box. The purple numbers are the fluxes (or rate of flow) to and from a box in gigatonnes of carbon per year (Gt/y).
A little quick counting shows that about 200 Gt C leaves and enters the atmosphere each year. As a first approximation then, given the reservoir size of 750 Gt, we can work out that the residence time of a given molecule of CO2 is 750 Gt C / 200 Gt C y-1 = about 3-4 years. (However, careful counting up of the sources (supply) and sinks (removal) shows that there is a net imbalance; carbon in the atmosphere is increasing by about 3.3 Gt per year).
It is true that an individual molecule of CO2 has a short residence time in the atmosphere. However, in most cases when a molecule of CO2 leaves the atmosphere it is simply swapping places with one in the ocean. Thus, the warming potential of CO2 has very little to do with the residence time of individual CO2 molecules in the atmosphere.
What really governs the warming potential is how long the extra CO2 remains in the atmosphere. CO2 is essentially chemically inert in the atmosphere and is only removed by biological uptake and by dissolving into the ocean. Biological uptake (with the exception of fossil fuel formation) is carbon neutral: Every tree that grows will eventually die and decompose, thereby releasing CO2. (Yes, there are maybe some gains to be made from reforestation but they are probably minor compared to fossil fuel releases).
Dissolution of CO2 into the oceans is fast but the problem is that the top of the ocean is “getting full” and the bottleneck is thus the transfer of carbon from surface waters to the deep ocean. This transfer largely occurs by the slow ocean basin circulation and turn over (*3). This turnover takes 500-1000ish years. Therefore a time scale for CO2 warming potential out as far as 500 years is entirely reasonable (See IPCC 4th Assessment Report Section 2.10).
Intermediate rebuttal written by Doug Mackie
Update July 2015:
Here is the relevant lecture-video from Denial101x - Making Sense of Climate Science Denial
Last updated on 5 July 2015 by pattimer. View Archives































 Arguments
Arguments


























 I will comment on the 7 year mean as a means of excluding the large amount of noise. Clearly both plots A and C have a number of small excursions from a constant value, no doubt attributable to fluctuations in global temperature and/or ENSO. Both also have a large excursion in the early 90's, no doubt attributable to the rapid cooling consequent on the major volcano at that time (Pinatubo?). But the plot of the draw down of CO2 against cumulative change in CO2 concentration shows two additional large excursions, one at the start, and one at the end, which are not present in the plot against a constant fraction of annual emissions.
Clearly then, the available evidence supports my (and Archer and Brovkin's) understanding over yours. While I doubt the evidence is conclusive, given the noisy nature of the data, none-the-less your position means you are arguing against both the evidence, against straightforward theoretical considerations, and against expert opinion. In that position, I would have very little confidence of the correctness of my position.
5) Finally, you quote the seasonal variation in CO2 concentrations as a disproof of my position. However, it is plain that the seasonal variations have a half cycle significantly less than the typical time to reach equilibrium with the surface. Therefore, while we would expect interactions with the ocean to dampen, we would not expect them to eliminate the cycle. Further, given that about a quarter of the annual emissions are absorbed by land, which violently fluctuates in temperature, moisture, and coverage over the course of the seasons, the land based processes may dampen, be neutral with, or amplify such a cycle. Given this, and given the lack of knowledge regarding the land based processes, and given that you cannot quantify the actual amount of CO2 emitted by decay of biota over Autumn and Winter so that we cannot predict the size of the cycle except by measuring it; we simply do not have enough information to run the argument you are trying to run.
That does not mean I have refuted this argument. But it does mean you have not provided a reason to disagree with the balance of evidence which is strongly against your position.
I will comment on the 7 year mean as a means of excluding the large amount of noise. Clearly both plots A and C have a number of small excursions from a constant value, no doubt attributable to fluctuations in global temperature and/or ENSO. Both also have a large excursion in the early 90's, no doubt attributable to the rapid cooling consequent on the major volcano at that time (Pinatubo?). But the plot of the draw down of CO2 against cumulative change in CO2 concentration shows two additional large excursions, one at the start, and one at the end, which are not present in the plot against a constant fraction of annual emissions.
Clearly then, the available evidence supports my (and Archer and Brovkin's) understanding over yours. While I doubt the evidence is conclusive, given the noisy nature of the data, none-the-less your position means you are arguing against both the evidence, against straightforward theoretical considerations, and against expert opinion. In that position, I would have very little confidence of the correctness of my position.
5) Finally, you quote the seasonal variation in CO2 concentrations as a disproof of my position. However, it is plain that the seasonal variations have a half cycle significantly less than the typical time to reach equilibrium with the surface. Therefore, while we would expect interactions with the ocean to dampen, we would not expect them to eliminate the cycle. Further, given that about a quarter of the annual emissions are absorbed by land, which violently fluctuates in temperature, moisture, and coverage over the course of the seasons, the land based processes may dampen, be neutral with, or amplify such a cycle. Given this, and given the lack of knowledge regarding the land based processes, and given that you cannot quantify the actual amount of CO2 emitted by decay of biota over Autumn and Winter so that we cannot predict the size of the cycle except by measuring it; we simply do not have enough information to run the argument you are trying to run.
That does not mean I have refuted this argument. But it does mean you have not provided a reason to disagree with the balance of evidence which is strongly against your position.







Climate Myth...