Arguments
A detailed look at climate sensitivity
Posted on 8 September 2010 by dana1981
Some global warming 'skeptics' argue that the Earth's climate sensitivity is so low that a doubling of atmospheric CO2 will result in a surface temperature change on the order of 1°C or less, and that therefore global warming is nothing to worry about. However, values this low are inconsistent with numerous studies using a wide variety of methods, including (i) paleoclimate data, (ii) recent empirical data, and (iii) generally accepted climate models.
Climate sensitivity describes how sensitive the global climate is to a change in the amount of energy reaching the Earth's surface and lower atmosphere (a.k.a. a radiative forcing). For example, we know that if the amount of carbon dioxide (CO2) in the Earth's atmosphere doubles from the pre-industrial level of 280 parts per million by volume (ppmv) to 560 ppmv, this will cause an energy imbalance by trapping more outgoing thermal radiation in the atmosphere, enough to directly warm the surface approximately 1.2°C. However, this doesn't account for feedbacks, for example ice melting and making the planet less reflective, and the warmer atmosphere holding more water vapor (another greenhouse gas).
Climate sensitivity is the amount the planet will warm when accounting for the various feedbacks affecting the global climate. The relevant formula is:
dT = ?*dF
Where 'dT' is the change in the Earth's average surface temperature, '?' is the climate sensitivity, usually with units in Kelvin or degrees Celsius per Watts per square meter (°C/[W m-2]), and 'dF' is the radiative forcing, which is discussed in further detail in the Advanced rebuttal to the 'CO2 effect is weak' argument.
Climate sensitivity is not specific to CO2
A common misconception is that the climate sensitivity and temperature change in response to increasing CO2 differs from the sensitivity to other radiative forcings, such as a change in solar irradiance. This, however, is not the case. The surface temperature change is proportional to the sensitivity and radiative forcing (in W m-2), regardless of the source of the energy imbalance.
In other words, if you argue that the Earth has a low climate sensitivity to CO2, you are also arguing for a low climate sensitivity to other influences such as solar irradiance, orbital changes, and volcanic emissions. Thus when arguing for low climate sensitivity, it becomes difficult to explain past climate changes. For example, between glacial and interglacial periods, the planet's average temperature changes on the order of 6°C (more like 8-10°C in the Antarctic). If the climate sensitivity is low, for example due to increasing low-lying cloud cover reflecting more sunlight as a response to global warming, then how can these large past climate changes be explained?
Figure 1: Antarctic temperature changes over the past 450,000 years as measured from ice cores
What is the possible range of climate sensitivity?
The IPCC Fourth Assessment Report summarized climate sensitivity as "likely to be in the range 2 to 4.5°C with a best estimate of about 3°C, and is very unlikely to be less than 1.5°C. Values substantially higher than 4.5°C cannot be excluded, but agreement of models with observations is not as good for those values."
Individual studies have put climate sensitivity from a doubling of CO2 at anywhere between 0.5°C and 10°C; however, as a consequence of increasingly better data, it appears that the extreme higher and lower values are very unlikely. In fact, as climate science has developed and advanced over time , estimates have converged around 3°C. A summary of recent climate sensitivity studies can be found here.
A study led by Stefan Rahmstorf concluded "many vastly improved models have been developed by a number of climate research centers around the world. Current state-of-the-art climate models span a range of 2.6–4.1°C, most clustering around 3°C" (Rahmstorf 2008). Several studies have put the lower bound of climate sensitivity at about 1.5°C,on the other hand, several others have found that a sensitivity higher than 4.5°C can't be ruled out.
A 2008 study led by James Hansen found that climate sensitivity to "fast feedback processes" is 3°C, but when accounting for longer-term feedbacks (such as ice sheet
disintegration, vegetation migration, and greenhouse gas release from soils, tundra or ocean), if atmospheric CO2 remains at the doubled level, the sensitivity increases to 6°C based on paleoclimatic (historical climate) data.
What are the limits on the climate sensitivity value?
Paleoclimate
The main limit on the sensitivity value is that it has to be consistent with paleoclimatic data. A sensitivity which is too low will be inconsistent with past climate changes - basically if there is some large negative feedback which makes the sensitivity too low, it would have prevented the planet from transitioning from ice ages to interglacial periods, for example. Similarly a high climate sensitivity would have caused more and larger past climate changes.
One recent study examining the Palaeocene–Eocene Thermal Maximum (about 55 million years ago), during which the planet warmed 5-9°C, found that "At accepted values for the climate sensitivity to a doubling of the atmospheric CO2 concentration, this rise in CO2 can explain only between 1 and 3.5°C of the warming inferred from proxy records" (Zeebe 2009). This suggests that climate sensitivity may be higher than we currently believe, but it likely isn't lower.
Recent responses to large volcanic eruptions
Climate scientists have also attempted to estimate climate sensitivity based on the response to recent large volcanic eruptions, such as Mount Pinatubo in 1991. Wigley et al. (2005) found:
"Comparisons of observed and modeled coolings after the eruptions of Agung, El Chichón, and Pinatubo give implied climate sensitivities that are consistent with the Intergovernmental Panel on Climate Change (IPCC) range of 1.5–4.5°C. The cooling associated with Pinatubo appears to require a sensitivity above the IPCC lower bound of 1.5°C, and none of the observed eruption responses rules out a sensitivity above 4.5°C."
Similarly, Forster et al. (2006) concluded as follows.
"A climate feedback parameter of 2.3 +/- 1.4 W m-2 K-1 is found. This corresponds to a 1.0–4.1 K range for the equilibrium warming due to a doubling of carbon dioxide"
Other Empirical Observations
Gregory et al. (2002) used observed interior-ocean temperature changes, surface temperature changes measured since 1860, and estimates of anthropogenic and natural radiative forcing of the climate system to estimate its climate sensitivity. They found:
"we obtain a 90% confidence interval, whose lower bound (the 5th percentile) is 1.6 K. The median is 6.1 K, above the canonical range of 1.5–4.5 K; the mode is 2.1 K."
Examining Past Temperature Projections
In 1988, NASA climate scientist Dr James Hansen produced a groundbreaking study in which he produced a global climate model that calculated future warming based on three different CO2 emissions scenarios labeled A, B, and C (Hansen 1988). Now, after more than 20 years, we are able to review Hansen’s projections.
Hansen's model assumed a rather high climate sensitivity of 4.2°C for a doubling of CO2. His Scenario B has been the closest to reality, with the actual total radiative forcing being about 10% higher than in this emissions scenario. The warming trend predicted in this scenario from 1988 to 2010 was about 0.26°C per decade whereas the measured temperature increase over that period was approximately 0.18°C per decade, or about 40% lower than Scenario B.
Therefore, what Hansen's models and the real-world observations tell us is that climate sensitivity is about 40% below 4.2°C, or once again, right around 3°C for a doubling of atmospheric CO2.
Probabilistic Estimate Analysis
Annan and Hargreaves (2009) investigated various probabilistic estimates of climate sensitivity, many of which suggested a "worryingly high probability" (greater than 5%) that the sensitivity is in excess of than 6°C for a doubling of CO2. Using a Bayesian statistical approach, this study concluded that
"the long fat tail that is characteristic of all recent estimates of climate sensitivity simply disappears, with an upper 95% probability limit...easily shown to lie close to 4°C, and certainly well below 6°C."
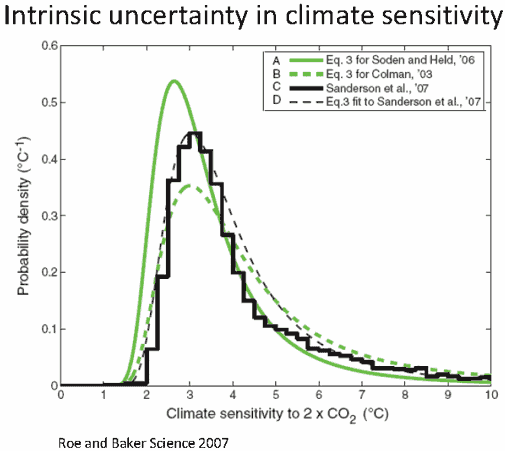
Figure 2: Probability distribution of climate sensitivity to a doubling of atmospheric CO2
Summary of these results
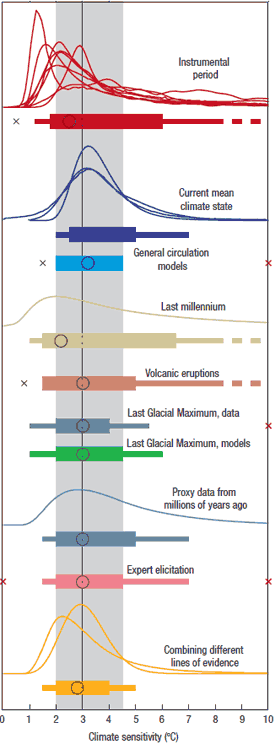
Knutti and Hegerl (2008) presents a comprehensive, concise overview of our scientific understanding of climate sensitivity. In their paper, they present a figure which neatly encapsulates how various methods of estimating climate sensitivity examining different time periods have yielded consistent results, as the studies described above show. As you can see, the various methodologies are generally consistent with the range of 2-4.5°C, with few methods leaving the possibility of lower values, but several unable to rule out higher values.
Figure 3: Distributions and ranges for climate sensitivity from different lines of evidence. The circle indicates the most likely value. The thin colored bars indicate very likely value (more than 90% probability). The thicker colored bars indicate likely values (more than 66% probability). Dashed lines indicate no robust constraint on an upper bound. The IPCC likely range (2 to 4.5°C) and most likely value (3°C) are indicated by the vertical grey bar and black line, respectively.
What does all this mean?
According to a recent MIT study, we're currently on pace to reach this doubled atmospheric CO2 level by the mid-to-late 21st century.
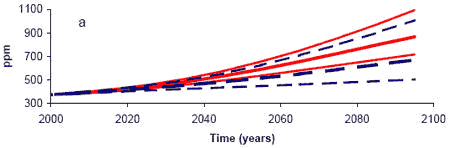
Figure 4: Projected decadal mean concentrations of CO2. Red solid lines are median, 5%, and 95% for the MIT study, the dashed blue line is the same from the 2003 MIT projection.
So unless we change course, we're looking at a rapid warming over the 21st century. Most climate scientists agree that a 2°C warming is the 'danger limit'. Figure 5 shows temperature rise for a given CO2 level. The dark grey area indicates the climate sensitivity likely range of 2 to 4.5°C.
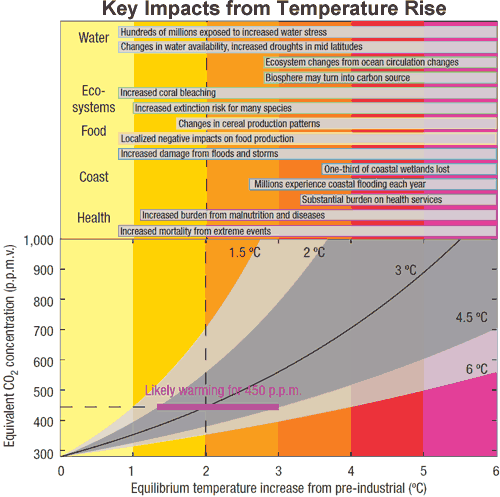
Figure 5: Relation between atmospheric CO2 concentration and key impacts associated with equilibrium global temperature increase. The most likely warming is indicated for climate sensitivity 3°C (black solid). The likely range (dark grey) is for the climate sensitivity range 2 to 4.5°C. Selected key impacts (some delayed) for several sectors and different temperatures are indicated in the top part of the figure.
If we manage to stabilize CO2 levels at 450 ppmv (the atmospheric CO2 concentration as of 2010 is about 390 ppmv), according to the best estimate, we have a probability of less than 50% of meeting the 2°C target. The key impacts associated with 2°C warming can be seen at the top of Figure 5. The tight constraint on the lower limit of climate sensitivity indicates we're looking down the barrel of significant warming in future decades.
As the scientists at RealClimate put it,"Global warming of 2°C would leave the Earth warmer than it has been in millions of years, a disruption of climate conditions that have been stable for longer than the history of human agriculture. Given the drought that already afflicts Australia, the crumbling of the sea ice in the Arctic, and the increasing storm damage after only 0.8°C of warming so far, calling 2°C a danger limit seems to us pretty cavalier."
This post is the Advanced version (written by dana1981) of the skeptic argument "Climate sensitivity is low". Note: a Basic version is on its way and should be published shortly.
0 
0
With a simple Zero-dimensional climate model it is very easy to demonstrate the effect.
The more uneven atmospheric water vapor distribution gets, the lower average surface temperature goes. For a realistic range of parameters, entropy production of the system also goes up as water vapor gets lumpy, even if heat distribution along the surface is extremely efficient (same surface temperature everywhere).
The main problem with analytic computational climate models is that they are unable to resolve these fine structures so they simply apply averages at sub-grid scales.
To put it in another way you can see through a barbed wire fence easily. But if you take the average density of iron per unit area, it gets indistinguishable from a thin but absolutely opaque iron plate.
Now, let's consider a very simple climate model. There are two layers, the surface and the atmosphere. In such a model atmospheric (absolute) temperature is always 0.84 times lower than surface temperature, because from there half the thermal radiation goes up, half down (and 0.84 ~ 2-1/4).
As in this model the path length is fixed, IR optical depth τ is proportional to the concentration of GHGs in the atmosphere. For the sake of simplicity, let's suppose it is independent of wavelength in thermal IR. In this case absorptivity/emissivity of the atmosphere is 1-e-τ. Also, let the atmosphere be transparent to short wave radiation.
If I is the short wave radiation flux at the surface and T is absolute temperature there (and the surface radiates as a black body in IR), then
I = (1+e-τ)/2·σ·T4 (σ is the Stefan–Boltzmann constant)
It is easy to see for a given SW flux I if IR optical depth τ is increased, T should go up as well.
However, let's make the model just a little bit more complicated. Let's have two compartments of equal area over which the sum of GHGs is constant but it may be different between them.
That is, in compartment A optical depth is 2τ·cos2φ and in compartment B it is 2τ·sin2φ (the average is τ of course). Also, let the heat transport between compartments be very efficient, so surface temperature T is the same everywhere.
In this case the effective optical depth is
τeff=-log((e-2τ·cos2φ+e-2τ·sin2φ)/2)
Now, τeff happen to have a maximum at φ=45° where GHG distribution is uniform between the compartments and decreases as it is getting more uneven.
Therefore a small increase in overall IR optical depth τ due to increased GHG concentration can be compensated for by making its distribution skewed. Water vapor, as a not well mixed GHG is perfect for this purpose.
I do not put expression for entropy production here, because it is a bit complicated. But you can figure it out yourself based on radiative entropy flux of a black body being 4/3·σ·T3.
Anyway, overall entropy production is also increased by decreasing τeff, so the maximum entropy production principle pushes the climate system toward an uneven GHG distribution whenever it is possible.
Note cloud albedo is not taken into account at all in this discussion, only clear sky water vapor distribution.
But back to your astonishment. You have probably heard of the Clay Institute's Millennium Prize Problems. These are extraordinarily hard and important mathematical problems, with a one million dollar prize for each (must be the least easy way to make a million bucks). Now, among these problems we can find the existence (or the lack of it) of well-behaved solutions of the Navier-Stokes Equation for reasonable initial conditions. These equations describe the motion of fluid substances, pretty basic stuff for e.g. GCMs, so the truly astonishing fact is that the science is not settled at all, not even the science of basic mathematical tools. And the existence problem of solutions to incompressible fluid motion is just the tip of the iceberg, there are many more unresolved tidbits around turbulent flows. Rather expensive wind tunnels are not maintained by mere accident in an age of supercomputers.
And now let's see what Tompkins did. He has recognized the fact GCM performance depends not only on average humidity in grid cells, but also on finer details of its distribution inside the cells, that is, on higher moments like variance and skewness (or kurtosis, although he fails to mention this one), just like I was trying to show you above.
Then, at least to my astonishment he proceeds as follows:
"From the brief review of statistical schemes it is apparent that a widely varying selection of PDFs [probability density functions] have been used. One reason for this is that it is difficult to obtain generalized and accurate information from observations concerning variability [of humidity] down to small scales"
Difficult, indeed. The traditional approach in cases like this is to consider the difficulty as a challenge and start working on ways to overcome it. It is quite astonishing how often this kind of attitude has been proven to be fertile.
But instead of aiming for actual data, he is trying to circumvent the problem by resorting to a CRM (Cloud Resolving Model). That is, instead of going out and having a look or two at what's going on in nature, he applies another computational model, this time on a smaller scale.
"The first aim of this paper therefore, is to use a 3D CRM, on domains on the order of a climate model grid box but also with relatively high horizontal resolution, to assess whether a generalized function form exists that can describe the total water variability"
It would not be such a serious problem had he not called running a program an experiment and program output data.
"Examination of the PDFs every half hour throughout the experiment proved them to be very similar in characteristics, since the computational domain was sufficient in size to continuously contain an ensemble of clouds, and the initial conditions were a realistic field of clouds in a state of quasi-equilibrium. The data at the 65 536 grid points are divided into 200 bins of equal width [etc., etc.]"
Of course Gedankenexperiments were always legitimate tools of the scientific inquiry, but they are not substitutes for actual experiments or observations. Traditionally they were never used to settle the science, but to uncover holes in existing theory (to be filled later by either reshaping the theory or collecting relevant data).
Note the CRM he has experimented with has the same Navier-Stokes equations in its belly, also gridded, therefore unable to handle sub-grid processes of its own. As flows tend to be turbulent down to microscopic scales (have you ever seen the fine threads of cigarette smoke?) and turbulence generates fractal structures, this model also has to be parametrized. In 3D flows (unlike in 2D ones) energy in small-scale eddies never gets negligible by shrinking through many orders of magnitude (this is the very reason behind the mathematical troubles).
So. Water vapor distribution statistics presented in this paper are neither rooted in first principles nor in actual observations, they just hover in thin air (they do what vapor is supposed to do after all).
Comments