The anthropogenic global warming rate: Is it steady for the last 100 years? Part 2.
Posted on 7 May 2013 by KK Tung
This is part 2 of a guest post by KK Tung, who requested the opportunity to respond to the SkS post Tung and Zhou circularly blame ~40% of global warming on regional warming by Dumb Scientist (DS).
In this second post I will review the ideas on the Atlantic Multidecadal Oscillation (AMO). I will peripherally address some criticisms by Dumb Scientist (DS) on a recent paper (Tung and Zhou [2013] ). In my first post, I discussed the uncertainty regarding the net anthropogenic forcing due to anthropogenic aerosols, and why there is no obvious reason to expect the anthropogenic warming response to follow the rapidly increasing greenhouse gas concentration or heating, as DS seemed to suggest.
For over thirty years, researchers have noted a multidecadal variation in both the North Atlantic sea-surface temperature and the global mean temperature. The variation has the appearance of an oscillation with a period of 50-80 years, judging by the global temperature record available since 1850. This variation is on top of a steadily increasing temperature trend that most scientists would attribute to anthropogenic forcing by the increase in the greenhouse gases. This was pointed out by a number of scientists, notably by Wu et al. [2011] . They showed, using the novel method of Ensemble Empirical Mode Decomposition (Wu and Huang [2009 ]; Huang et al. [1998] ), that there exists, in the 150-year global mean surface temperature record, a multidecadal oscillation. With an estimated period of 65 years, 2.5 cycles of such an oscillation was found in that global record (Figure 1, top panel). They further argued that it is related to the Atlantic Multi-decadal Oscillation (AMO) (with spatial structure shown in Figure 1, bottom panel).
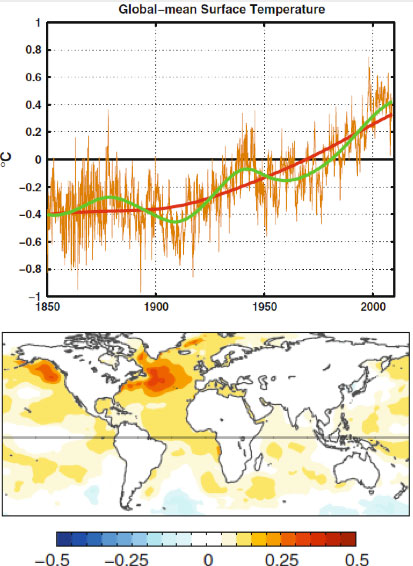
Figure 1. Taken from Wu et al. [2011] . Top panel: Raw global surface temperature in brown. The secular trend in red. The low-frequency portion of the data constructed using the secular trend plus the gravest multi-decadal variability, in green. Bottom panel: the global sea-surface temperature regressed onto the gravest multi-decadal mode.
Less certain is whether the multidecadal oscillation is also anthropogenically forced or is a part of natural oscillation that existed even before the current industrial period.
It is now known that the AMO exists in coupled atmosphere-ocean models without anthropogenic forcing (i.e. in “control runs”, in the jargon of the modeling community). It is found, for example in a version of the GFDL model at Princeton, and the Max Planck model in Germany. Both have the oscillation of the right period. In the models that participated in IPCC’s Fourth Assessment Report (AR4), no particular attempt was given to initialize the model’s oceans so that the modeled AMO would have the right phase with respect to the observed AMO. Some of the models furthermore have too short a period (~20-30 years) in their multidecadal variability for reasons that are not yet understood. So when different runs were averaged in an ensemble mean, the AMO-like internal variability is either removed or greatly reduced. In an innovative study, DelSol et al. [2011] extract the spatial pattern of the dominant internal variability mode in the AR4 models. That pattern (Figure 2, top panel) resembles the observed AMO, with warming centered in the North Atlantic but also spreading to the Pacific and generally over the Northern Hemisphere (Delworth and Mann [2000] ).
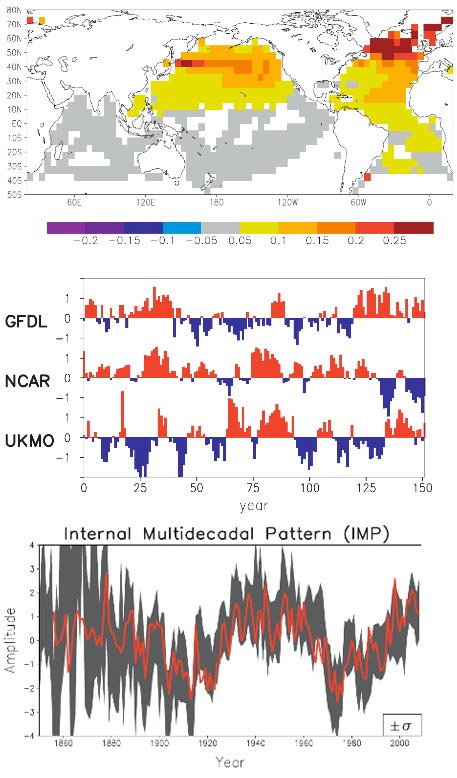
Figure 2. Taken from DelSol et al. [2011] . Top panel: the spatial pattern that maximizes the average predictability time of sea-surface temperature in 14 climate models run with fixed forcing (i.e. “control runs”). Middle panel: the time series of this component in three representative control runs. Bottom panel: time series obtained by projecting the observed data onto the model spatial pattern from the top panel. The red curve in the bottom panel is the annual average AMO index after scaling.
When the observed temperature is projected onto this model spatial pattern, the time series (in Figure 2 bottom panel) varies like the AMO Index (Enfield et al. [2001] ), even though individual models do not necessarily have an oscillation that behaves exactly like the AMO Index (Figure 2, middle panel).
There is currently an active debate among scientists on whether the observed AMO is anthropogenically forced. Supporting one side of the debate is the model, HadGEM-ES2, which managed to produce an AMO-like oscillation by forcing it with time-varying anthropogenic aerosols. The HadGEM-ES2 result is the subject of a recent paper by Booth et al. [2012] in Nature entitled “Aerosols implicated as a prime driver of twentieth-century North Atlantic climate variability”. The newly incorporated indirect aerosol effects from a time-varying aerosol forcing are apparently responsible for driving the multi-decadal variability in the model ensemble-mean global mean temperature variation. Chiang et al. [2013] pointed out that this model is an outlier among the CMIP5 models. Zhang et al. [2013] showed evidence that the indirect aerosol effects in HadGEM-ES2 have been overestimated. More importantly, while this model has succeeded in simulating the time behavior of the global-mean sea surface temperature variation in the 20th century, the patterns of temperature in the subsurface ocean and in other ocean basins are seen to be inconsistent with the observation. There is a very nice blog by Isaac Held of Princeton, one of the most respected climate scientists, on the AMO debate here. Held further pointed out the observed correlation between the North Atlantic subpolar temperature and salinity which was not simulated with the forced model: “The temperature-salinity correlations point towards there being a substantial internal component to the observations. These Atlantic temperature variations affect the evolution of Northern hemisphere and even global means (e.g., Zhang et al 2007). So there is danger in overfitting the latter with the forced signal only.”
The AMOC and the AMO
The salinity-temperature co-variation that Isaac Held mentioned concerns a property of the Atlantic Meridional Overturning Circulation (AMOC) that is thought to be responsible for the AMO variation at the ocean surface. This Great Heat Conveyor Belt connects the North Atlantic and South Atlantic (and other ocean basins as well), and between the warm surface water and the cold deep water. The deep water upwells in the South Atlantic, probably due to the wind stress there (Wunsch [1998] ). The upwelled cold water is transported near the surface to the equator and then towards to the North Atlantic all the way to the Arctic Ocean, warmed along the way by the absorption of solar heating. Due to evaporation the warmed water from the tropics is high in salt content. (So at the subpolar latitudes of the North Atlantic, the salinity of the water could serve as a marker of where the water comes from, if the temperature AMO is due to the variations in the advective transport of the AMOC. This behavior is absent if the warm water is instead forced by a basin wide radiative heating in the North Atlantic.) The denser water sinks in the Arctic due to its high salt content. In addition, through its interaction with the cold atmosphere in the Arctic, it becomes colder, which is also denser. There are regions in the Arctic where this denser water sinks and becomes the source of the deep water, which then flows south. (Due to the bottom topography in the Pacific Arctic most of the deep water flows into the Atlantic.) The Sun is the source of energy that drives the heat conveyor belt. Most of the solar energy penetrates to the surface in the tropics, but due to the high water-vapor content in the tropical atmosphere it is opaque to the back radiation in the infrared. The heat cannot be radiated away to space locally and has to be transported to the high latitudes, where the water vapor content in the atmosphere is low and it is there that the transported heat is radiated to space.
In the North Atlantic Arctic, some of the energy from the conveyor belt is used to melt ice. In the warm phase of the AMO, more ice is melted. The fresh water from melting ice lowers the density of the sinking water slightly, and has a tendency to slow the AMOC slightly after a lag of a couple decades, due to the great inertia of that thermohaline circulation. A slower AMOC would mean less transport of the tropical warm water at the surface. This then leads to the cold phase of the AMO. A colder AMO would mean more ice formation in the Arctic and less fresh water. The denser water sinks more, and sows the seed for the next warm phase of the AMO. This picture is my simplified interpretation of the paper by Dima and Lohmann [2007] and others. The science is probably not yet settled. One can see that the physics is more complicated than the simple concept of conserved energy being moved around, alluded to by DS. The Sun is the driver for the AMOC thermohaline convection, and the AMO can be viewed as instability of the AMOC (limit cycle instability in the jargon of dynamical systems as applied to simple models of the AMOC).
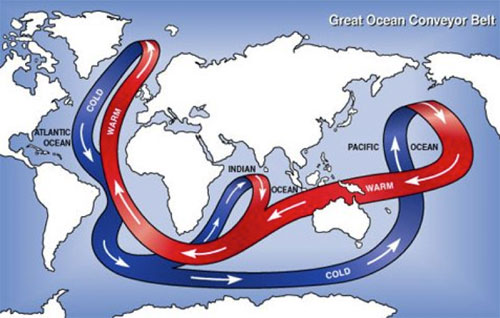
Figure 3. The great ocean conveyor belt. Schematic figure taken from Wikipedia.
Preindustrial AMO
It is fair to conclude that no CMIP3 or CMIP5 models have successfully simulated the observed multidecadal variability in the 20th century using forced response. While this fact by itself does not rule out the possibility of an AMO forced by anthropogenic forcing, it is not “unphysical” to examine the other possibility, that the AMO could be an internal variability of our climate system. Seeing it in models without anthropogenic forcing is one evidence. Seeing it in data before the industrial period is another important piece of evidence in support of it being a natural variability. These have been discussed in our PNAS paper. Figure 4 below is an updated version (to include the year 2012) of a figure in that paper. It shows this oscillation extending back as far as our instrumental and multi-proxy data can go, to 1659. Since this oscillation exists in the pre-industrial period, before anthropogenic forcing becomes important, it plausibly argues against it being anthropogenically forced.
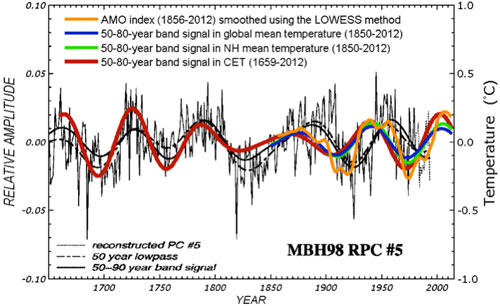
Figure 4. Comparison of the AMO mode in Central England Temperature (CET) (red) and in global mean (HadCRUT4) (blue), obtained from Wavelet analysis, with the multi-proxy AMO of Delworth and Mann [2000] (in thin black line). The amplitude of multi-proxy data is only relative (left axis). The orange curve is a smoothed version of the AMO index originally available in monthly form.
The uncertainties related to this result are many, and these were discussed in the paper but worth highlighting here. One, there is no global instrumental data before 1850. Coincidentally, 1850 is considered the beginning of the industrial period (the Second Industrial Revolution, when steam engines spewing out CO2 from coal burning were used). So pre-industrial data necessarily need to come from nontraditional sources, and they all have problems of one sort of the other. But they are all we have if we want to have a glimpse of climate variations before 1850. The thermometer record collected at Central England (CET) is the longest such record available. It cannot be much longer because sealed liquid thermometers were only invented a few years earlier. It is however a regional record and does not necessarily represent the mean temperature in the Northern Hemisphere. This is the same problem facing researchers who try to infer global climate variations using ice-core data in the Antarctica. The practice has been to divide the low-frequency portion of that polar data by a scaling factor, usually 2, and use that to represent the global climate. While there has been some research on why the low-frequency portion of the time series should represent a larger area mean, no definitive proof has been reached, and more research needs to be done. We know that if we look at the year-to-year variations in winters of England, one year could be cold due to a higher frequency of local blocking events, while the rest of Europe may not be similarly cold. However, if England is cold for 50 years, say, we know intuitively that it must have involved a larger scale cooling pattern, probably hemispherically wide. That is, England’s temperature may be reflecting a climate change. We tried to demonstrate this by comparing low passed CET data and global mean data, and showed that they agree to within a scaling factor slightly larger than one. England has been warming in the recent century, as in the global mean. It even has the same ups and downs that are in the hemispheric mean and global mean temperature (see Figure 4).
In the pre-industrial era, the comparison used in Figure 4 was with the multiproxy data of Delworth and Mann [2000]. These were collected over geographically distributed sites over the Northern Hemisphere, and some, but very few, in the Southern Hemisphere. They show the same AMO-like behavior as in CET. CET serves as the bridge that connects preindustrial proxy data with the global instrumental data available in the industrial era. The continuity of CET data also provides a calibration of the global AMO amplitude in the pre-industrial era once it is calibrated against the global data in the industrial period. The evidence is not perfect, but is probably the best we can come up with at this time. Some people are convinced by it and some are not, but the arguments definitely were not circular.
How to detrend the AMO Index
The mathematical issues on how best to detrend a time series were discussed in the paper by Wu et al. [2007] in PNAS. The common practice has been to fit a linear trend to the time series by least squares, and then remove that trend. This is how most climate indices are defined. Examples are QBO, ENSO, solar cycle etc. In particular, similar to the common AMO index, the Nino3.4 index is defined as the mean SST in the equatorial Pacific (the Nino3.4 region) linearly detrended. Another approach uses leading EOF in the detrended data for the purpose of getting the signal with the most variance. An example is the PDO. One can get more sophisticated and adaptively extract and then subtract a nonlinear secular trend using the method of EMD discussed in that paper. Either way you get almost the same AMO time series from the North Atlantic mean temperature as the standard definition of Enfield et al. [2001] , who subtracted the linear trend in the North Atlantic mean temperature for the purpose of removing the forced component. There were concerns raised (Trenberth and Shea [2006 ]; Mann and Emanuel [2006] ) that some nonlinear forced trends still remain in the AMO Index. Enfield and Cid-Serrano [2010] showed that removing a nonlinear (quadratic) trend does not affect the multidecadal oscillation. Physical issues on how best to define the index are more complicated. Nevertheless if what you want to do is to detrend the North Atlantic time series it does not make sense to subtract from it the global-mean time variation. That is, you do not detrend time series A by subtracting from it time series B. If you do, you are introducing another signal, in this case, the global warming signal (actually the negative of the global warming signal) into the AMO index. There may be physical reasons why you may want to define such a composite index, but you have to justify that unusual definition. Trenberth and Shea [2006] did it to come up with a better predictor for a local phenomenon, the Atlantic hurricanes. An accessible discussion can be found in Wikipedia. http://en.wikipedia.org/wiki/Atlantic_multidecadal_oscillation
The amplitude of the oscillatory part of the North Atlantic mean temperature is larger than that in the global mean, but its long-term trend is smaller. So if the global mean variation is subtracted from the North Atlantic mean, the oscillation still remains at 2/3 the amplitude but a negative trend is created. K.a.r.S.t.e.N provided a figure in post 30 here. I took the liberty in reposting it below. One sees that the multidecadal oscillation is still there. But the negative trend in this AMO index causes problems with the multiple linear regression (MLR) analysis, as discussed in part 1 of my post.
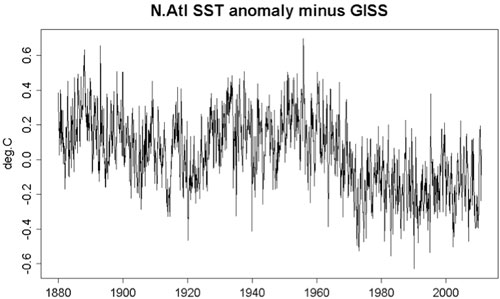
Figure 5: North Atlantic SST minus the global mean.
From a purely technical point, the collinearity introduced between this negative trend in the AMO index and the anthropogenic positive trend confuses the MLR analysis. If you insist on using it, it will give a 50-year anthropogenic trend of 0.1 degree C/decade and a 34-year anthropogenic trend of 0.125 degree C/decade. The 50-year trend is not too much larger than what we obtained previously but these numbers cannot be trusted.
One could suggest, qualitatively, that the negative trend is due to anthropogenic aerosol cooling and the ups and down due to what happens before and after the Clean Air Act etc. But these arguments are similar to the qualitative arguments that some have made about the observed temperature variations as due to solar radiation variations. To make it quantitative we need to put the suggestion into a model and check it against observation. This was done by the HadGEM-ES2 model, and we have discussed above why it has aspects that are inconsistent with observation.
The question of whether one should use the AMO Index as defined by Enfield et al. [2001] or by Trenberth and Shea [2006] was discussed in detail in Enfield and Cid-Serrano [2010] , who argued against the latter index as “throwing the baby out with the bath water”. In effect this is a claim of circular argument. They claimed that this procedure is valid “only if it is known a priori that the Atlantic contribution to the global SST signal is entirely anthropogenic, which of course is not known”. Charges of circular argument have been leveled at those adopting either AMO index in the past, and DumbScientist was not the first. In my opinion, the argument should be a physical one and one based on observational evidence. An argument based on one definition of the index being self-evidently correct is bound to be circular in itself. Physical justification of AMO being mostly natural or anthropogenically forced needs to precede the choice of the index. This was what we did in our PNAS paper.
Enfield and Cid-Serrano [2010] also examined the issue of causality and the previous claim by Elsner [2006] that the global mean temperature multidecadal variation leads the AMO. They found that the confusion was caused by the fact that Elsner used a 1-year lag to annualized data: While the ocean (AMO) might require upwards of a year to adjust to the atmosphere, the atmosphere responds to the ocean in less than a season, essentially undetectable with a 1-year lag. The Granger test with annual data will fail to show the lag of the atmosphere, thus showing the global temperature to be causal.
What is an appropriate regressor/predictor?
There is a concern that the AMO index used in our multiple regression analysis is a temperature response rather than a forcing index. Ideally, all predictors in the analysis should be external forcings, but compromises are routinely made to account for internal variability. The solar forcing index is the solar irradiance measured outside the terrestrial climate system, and so is a suitable predictor. Carbon dioxide forcing is external to the climate system as humans extract fossil fuel and burn it to release the carbon. Volcanic aerosols are released from deep inside the earth into the atmosphere. In the last two examples, the forcing should actually be internal to the terrestrial system, but is considered external to the atmosphere-ocean climate system in a compromise. Further compromise is made in the ENSO “forcing”. ENSO is an internal oscillation of the equatorial Pacific-atmosphere system, but is usually treated as a “forcing” to the global climate system in a compromise. A commonly used ENSO index, the Nino3.4 index, is the mean temperature in a part of the equatorial Pacific that has a strong ENSO variation. It is not too different than the Multivariate ENSO Index used by Foster and Rahmstorf [2011] . It is in principle better to use an index that is not temperature, and so the Southern Oscillation Index (SOI), which is the pressure difference between Tahiti and Darwin, is sometimes used as a predictor for the ENSO temperature response. However, strictly speaking, the SOI is not a predictor of ENSO, but a part of the coupled atmosphere-ocean response that is the ENSO phenomenon. In practice it does not matter much which ENSO index is used because their time series behave similarly. It is in the same spirit that the AMO index, which is a mean of the detrended North Atlantic temperature, is used to predict the global temperature change. It is one step removed from the global mean temperature being analyzed. A better predictor should be the strength of the AMOC, whose variation is thought to be responsible for the AMO. However, measurements deep ocean circulation strength had not been available. Recently Zhang et al. [2011] found that the North Brazil Current (NBC) strength, measured off the coast of Brazil, could be a proxy for the AMOC, and they verified it with a 700-year model run. We could have used NBC as our predictor for the AMO, but that time series is available only for the past 50 years, not long enough for our purpose. They however also found that the NBC variation is coherent with the AMO index. So for our analysis for the past 160 years, we used the AMO index. This is not perfect, but I hope the readers will understand the practical choices being made.
References
Booth, B. B. B., N. J. Dunstone, P. R. Halloran, T. Andrews, and N. Bellouin, 2012: Aerosols implicated as a prime dirver of twentieth-century North Atlantic climate variability. Nature, 484, 228-232.
Chiang, J. C. H., C. Y. Chang, and M. F. Wehner, 2013: Long-term behavior of the Atlantic interhemispheric SST gradient in the CMIP5 historial simulations. J. Climate, submitted.
DelSol, T., M. K. Tippett, and J. Shukla, 2011: A significant component of unforced multidecadal variability in the recent acceleration of global warming. J. Climate, 24, 909-026.
Delworth, T. L. and M. E. Mann, 2000: Observed and simulated multidecadal variability in the Northern Hemisphere. Clim. Dyn., 16, 661-676.
Elsner, J. B., 2006: Evidence in support of the climatic change-Atlantic hurricane hypothesis. Geophys. Research. Lett., 33, doi:10.1029/2006GL026869.
Enfield, D. B. and L. Cid-Serrano, 2010: secular and multidecadal warmings in the North Atlantic and their relationships with major hurricane activity. Int. J. Climatol., 30, 174-184.
Enfield, D. B., A. M. Mestas-Nunez, and P. J. Trimble, 2001: The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental U. S. Geophys. Research. Lett., 28, 2077-2080.
Foster, G. and S. Rahmstorf, 2011: Global temperature evolution 1979-2010. Environmental Research Letters, 6, 1-8.
Huang, N. E., Z. Shen, S. R. Long, M. L. C. Wu, H. H. Shih, Q. N. Zheng, N. C. Yen, C. C. Tung, and H. H. Liu, 1998: The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London Ser. A-Math. Phys. Eng. Sci., 454, 903-995.
Mann, M. E. and K. Emanuel, 2006: Atlantic hurricane trends linked to climate change. Eos, 87, 233-244.
Trenberth, K. E. and D. J. Shea, 2006: Atlantic hurricanes and natural variability in 2005. Geophys. Research. Lett., 33, doi:10.1029/2006GL026894.
Tung, K. K. and J. Zhou, 2013: Using Data to Attribute Episodes of Warming and Cooling in Instrumental Record. Proc. Natl. Acad. Sci., USA, 110.
Wu, Z. and N. E. Huang, 2009: Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv. Adapt. Data Anal., 1, 1-14.
Wu, Z., N. E. Huang, S. R. Long, and C. K. Peng, 2007: On the trend, detrending and variability of nonlinear and non-stationary time series. Proc. Natl. Acad. Sci., USA, 104, 14889-14894.
Wu, Z., N. E. Huang, J. M. Wallace, B. Smoliak, and X. Chen, 2011: On the time-varying trend in global-mean surface temperature. Clim. Dyn.
Wunsch, C., 1998: The work done by the wind on the oceanic general circulation. J. Phys. Oceanography, 28, 2332-2340.
Zhang, D., R. Msadeck, M. J. McPhaden, and T. Delworth, 2011: Multidecadal variability of the North Brazil Current and its connection to the Atlantic meridional overtuning circulation. J. Geophys. Res.,, 116, doi:10.1029/2010JC006812.
Zhang, R., T. Delworth, R. Sutton, D. L. R. Hodson, K. W. Dixon, I. M. H. Held, Y., J. Marshall, Y. Ming, R. Msadeck, J. Robson, A. J. Rosati, M. Ting, and G. A. Vecchi, 2013: Have aerosols caused the observed Atlantic Multidecadal Variability? J. Atmos. Sci., 70, doi:10.1175/JAS-D-12-0331.1.































 Arguments
Arguments






























Prof. Tung. I deliberately separated the example from the discussion of AMO and relabelled the variables essentially at your request. The discussion is focussed on the form of the regression analysis, the exact nature of the variables is entirely unimportant, except for the fact that one of the variables (D) is only observed (C) in a form that is contaminated with the other two (A and B). Please can you answer the question, as posed: do you agree that in this example, the MLR regression method significantly underestimates the effect of signal A on signal Y?
please accept my appologies, I'm obviously having a bad day and am too grumpy to be posting. There was an error, it should be
B = 0.1*sin(2*pi*T/150);
however, the exact nature of the signals is unimportant other than that D is only observed contaminated with A and B as signal C. The plots and confidence intervals etc. should be O.K.
KK Tung @149.
Well, here is the statement from your first SkS Post and, as written, its context is quite clear. Figure 3 applies to the "final adjusted data" not to the "first step," not to any "intermediate step." Yet the presence of the "minor negative trend" is clearly accepted and while the rest of it is plainly described as "almost just noise" despite it still containing half the de-trended signal for 90 years of the 160 year of the MLR (as shown @148 above). This situation is described as "successful."
The arbitrary comment is made that this "small negative trend" can be added back from residual into anthropogenic regressor, but as written this is continuing to treat the "small negative trend" as one entirely negligable in consequence (because no consequences are described).
My Monte Carlo histograms estimated the confidence intervals. To make these 95% confidence intervals more explicit, gaussians are now fit to the histograms. For comparison, 95% confidence intervals from the post-1979 trend regressions are also reported now.
My original timeseries were simply chosen to look like these real timeseries from GISS and NOAA.
I wrote a new R program that downloads the HadCRUT4 annual global surface temperatures, and calculates annual averages of NOAA's long monthly AMO index and N. Atlantic SST:
The correlation coefficient between annual HadCRUT4 and N. Atlantic SST is 0.79. Linear regression is based on correlations, so my original synthetic timeseries were too highly correlated. Thanks for pointing this out, Dr. Tung.
In my original simulation, the regional variance was already larger than the global mean variance because the regional noise was added to the global noise. In reality, the annual N. Atlantic SST variance is 0.04°C^2 but the annual global HadCRUT4 variance is 0.07°C^2. Adding 0.3°C of regional noise yields a reasonable correlation coefficient, but it doesn't look realistic:
That looked more realistic but the average correlation coefficient over 10,000 runs was 0.64±0.08, which is too small. So I chose new simulation parameters to match the real correlation coefficient (0.79) and produce more realistic timeseries:
human = (t-t[1])^7
human = 0.7*human/human[length(t)]
nature = 0.15*cos(2*pi*(t-2000)/70)
global = human + nature + rnorm(t,mean=0,sd=0.11)
n_atlantic = human + nature + rnorm(t,mean=0,sd=sqrt(0.11^2+0.11^2))
Now the AMO's amplitude is 0.15°C and the total human contribution is 0.7°C, both of which match the lower bounds in Tung and Zhou 2013. The nonlinearity is now 7th order to keep the true post-1979 human trend at 0.17°C/decade.
Averaged over 10,000 Monte Carlo runs, the synthetic correlation coefficient was 0.74±0.06, which contains the real value (0.79). The synthetic global variance is 0.06±0.01°C^2 which contains the real value (0.07°C^2). The synthetic N. Atlantic variance is 0.07±0.01°C^2, which is still larger than the real value (0.04°C^2). However, the discrepancy has shrunk and the LOWESS smooth removes fast fluctuations anyway.
A 25-year LOWESS smooth was applied to the real and synthetic AMO index to match your paper:
smoothed_amo = lowess(t,amo,f=25/n)$y
amo = smoothed_amo
Here are the real residuals:
Here are the synthetic residuals:
Here are the real results:
(For easier comparison, the true human curve was shifted so it has the same post-1979 mean as the estimated human trend.)
Those results only use a white-noise model for comparison to the simulations. The real data are autocorrelated, and the caption of Fig. 1 in Zhou and Tung 2012 says the noise is order AR(4), which yields a trend of +0.12±0.05°C/decade.
Here are the synthetic results:
Averaged over 10,000 runs, the synthetic post-1979 trends and 95% confidence intervals are +0.09±0.04°C/decade. This histogram provides another similar estimate:
The true quadratic term is +5.15x10^(-5)°C/year^2, but the estimated value and its 95% confidence interval is +3.24±0.72x10^(-5)°C/year^2. The estimated human influence is still signficantly more linear than the true human influence, which is actually 7th order.
Despite smoothing the AMO index and choosing simulation parameters that yield timeseries and correlation coefficients that are more realistic, the true post-1979 trend of 0.17°C/decade is still above the 95% confidence interval. The same procedure applied to real data yields similar trends and uncertainties. Therefore, I still think Tung and Zhou 2013 is a circular argument.
The wavelet method is just another way to curve-fit, which is also inadequate because attribution is really a thermodynamics problem. Again, your curve-fitting claim that ~40% of the surface warming over the last 50 years can be attributed to a single mode of internal variability contradicts Isaac Held and Huber and Knutti 2012 who used thermodynamics to conclude that all modes of internal variability couldn't be responsible for more than about 25% of this surface warming.
In reply to Dikran Marsupial on the thought experiment he posed on post 134: I have a little time today and can get back to understand your thought experiment as I promised.
Conclusion: A conflated D and an error in plotting the deduced Anthropogenic response. But basically this is the trivial case that I had already discussed on post 124, this being the deterministic limit of Dumb Scientist's example.
In the thought experiment that you posed and later abandoned in favor of this one, there was a nonexistent AMO. This time there is an "unobserved signal D". I don't understand why you need it. Anyway, let's keep it but realize that D is simply the same sinusoid as B unless there was a typo. So it can be replaced by B. The problem is then rather simple:
Y is supposed to be your global mean data:
Y=A+1.5*B+0.1*radn(size(T)),
where A is his anthropogenic trend, with a quadratic term:
A=0.00002*(T+T.^2)
B is a natural oscillation:
B=0.1*sin(3.7*pi*T/150).
C is supposed to be your N. Atlantic mean temperature that you will use to define the AMO index, but there is no noise term. This is a major defect.
C=0.5*A+B.
Cd is C linear detrended, so it is
Cd=0.5*(A-beta(2)*T)+B=0.5*0.00002*T.^2+B
C and Cd are deterministic, and so this is a trivial case. No need to do MLR. (This is similar to the case of DS when the regional Atlantic noise is set to zero). I can solve this problem exactly to yield:
Y-1.5*Cd=0.00002*(T+0.25*t.^2)+0.1*radn(size(T)).
This is the same as your deduced A plus residual that you plotted in green line in your last figure. This is almost linear as you found because the quadratic term is 1/4 the original value in A. So it looks like the blue linear trend you draw in that figure.
The reason the blue line and greenline are offset below the red line A is that in your MLR X you have subtracted the mean of T, and so T does not start at 0 at year 0, but is zero at year 75. You can see it in the blue line in your last figure. Your claim that it falls outside the confidence interval is probably caused by this offset error.
In any case, regardless of the confidence level (which I have not checked because I did not repeat the MLR), you have not come up with a credible thought experiment to make your case against our MLR procedure. The present one is the same as a trivial subcase of Dumb Scientist's example that I discussed in my post 124. It is also very unrealistic because you did not include a noise term in your N. Atlantic data.
In reply to Dikran Marsupial on post 151. My reply to your post 134 is post 154. It was sent before I saw your correction to your D in the new post 151. It may be confusing because it arrived after your post 151.
Now with the correction, D has a different period as B. I still don't know what you intended it to be. In any case C is deterministic and that is the major defect of the thought experiment. The whole problem can still be solved algebraically. The criticism of your experiment in my post 134 still stands. If you wish I can repeat it with the correction in B that you just told me. But it is probably not necessary.
KK Tung wrote: "In any case C is deterministic and that is the major defect of the thought experiment."
This is irrelevant to the central point.
"The whole problem can still be solved algebraically."
It is irrelevant whether the problem can be solved algebraically, we are discussing a limitation of MLR, so the solution that MLR finds is the issue.
"The criticism of your experiment in my post 134 still stands. If you wish I can repeat it with the correction in B that you just told me."
Yes, please do so.
In reply to Dikran Marsupial's post 156: Before I do, do you agree with me that there was an error in your last figure showing that your deduced trend is outside the confidence level of the true value? I think it was a plotting problem, specifically a problem of offset, as I tried to point out to you. I wasn't sure of course because I didn't have the details.
KKTung@157 No, the confidence interval is for the gradient of the blue line, so the offset has no bearing on this whatsoever. I could add an offset to make the plots look more similar, but that would not change the conclusion that the MLR method significantly underestimates the effect of signal A on signal Y.
UPDATE: If the mean is not subtracted from Y, you get this
which still shows (even more clearly) that the deduced effect of A on Y (in blue) underestimates the actual effect of A on Y (red). There is a small difference in the confidence interval due to a different sample of noise, but it still doesn't contain the correct value (0.00304).
In reply to Dikran Marsupial in post 158: Although you did not admit it explicitly here, you seem to agree that there was an error, at least an inconsistency, in how you offset the red curve and the blue and green curves. In your post 123, you used your last figure, with an inconsistent offset, to show that the true A is above the blue and the green, leading to your conclusion:
"The deduced anthropogenic trend is less than the true value, and the true value does not lie within the confidence interval."
You may have other evidence that you did not show for this conclusion (and I don't quite understand your definition of the CI as from the gradient of the blue line), but your post 123 used only an erroneous figure to draw this visual conclusion. The corrected figure in your post 158 now shows that it is no longer visually obvious. In fact the true A (the redl ine) lies within the deduced adjusted data (green curve), which you labelled as deduced trend plus residual. I don't know what your blue curve is. It was not what we used. It appears to be a 150 year trend. If that is what it is, then it seems to be doing fine compared to the 150 year linear trend of true A. Please let me know if my understand is correct. I want to know what I am arguing against.
I will try later to address the issue why a deterministic example is trivial and why it is irrelevant as an example to argue your point. I just don't want to argue against an example with minor errors that you could correct easily.
Prof Tung. I said quite explicitly that there was no error. The attribution of Y to A depends on the identification of the correct value for the regression coefficients, which gives the GRADIENT of the signals, and the offset is irrelevant.
The confidence interval defined by your MLR procedure does not contain the true value, and therefore the MLR procedure is demonstrably unreliable.
I don't understand how anyone could look at the plot shown in my post #158 and come to the conclusion that the blue line is not an under-estimate of the signal shown in red, the average slope of the red line is clearly greater than that of the blue, and this is reflected in the confidence interval not containing the true value.
[Dirkan Marsupial] Error spotted by Leto corrected.
Dikran: I am not even sure what your blue line is. How can I then "come to the conclusion that it is the underestimate of the signal in red"? I thought we are supposed to be comparing the adjusted data (green curve), which is the regressed signal with the residual added back following our procedure in our paper (I assume you were following our procedure), against the true signal which is the red line.
The offset is relevant because once you corrected an inconsistent offset of the green vs the red, the two are much closer in your new figure compared to your old.
KK Tung The blue line is the linear trend for the "deduced anthropogenic signal" calculated from your MLR procedure, the green signal is this deduced anthropogenic signal with the residuals of the model added to it.
If you do not understand what the blue line is, perhaps you need to try to understand the thought experiment first before criticising as your criticisms have consistently demonstrated that you do not understand the point that has been made. Communicating that point has been made much more difficult by your constistant refusal to give a direct answer to the questions I have posed. If you give direct answers to these questions it makes it much easier to understand your position, so it is to your advantage to answer them.
The confidence interval 0.00204 +/- 0.00039 is the interval for the trend of the deduced A plus residual signal. Does this interval contain the true value 0.00304 representing the trend of the actual A signal? Yes or No?
Dikran, there seems to be an editing mishap in your post @160:
"the average slope of the red line is clearly greater than that of the red, and this is reflected in the confidence interval not containing the true value."
The average slope of the red line is greater than that of the blue.
[DikranMarsupial] Many thanks, I shall correct the error.
Dr. Tung - I believe that Dikran has shown the results of incorrect fixing/definition of a component in MLR. In the meantime, I would point out that all of this is based on a discussion of a central element in your paper:
Since your estimate of anthropogenic contributions is directly dependent on your estimate of the timing and scale of the AMO, a scale in conflict with other investigators, thermodynamics and PCA, I (and others commenting on this thread) cannot agree with your conclusions regarding the size of those anthropogenic contributions.
Arguing about the fine details of thought experiments, as above, does not change the fact that incorrect fixation of a signal component will lead to incorrect estimates of other components from that signal. And there is considerable evidence indicating just such an incorrect fixation of the AMO component in your work.
Just a short reply to the last few posts: I am trying to move on to other threads, such as responding to Dumb Scientist's post and reviewing other publications on the so-called "thermodynamic argument", but I have been bogged down arguing with Dikran. I had hoped that it would have been done and then I could move on, but he kept changing his example, making mistakes/typos/inconsistent offsets along the way. I would write another longer post about my understanding of his thought experiment. Here I just want to say that he is comparing something, specifically his blue line, which was not part of what our papers were concerned about. In observation, the total heating over the past 100 years is about 0.7 C, which is the same as what our deduced anthopogenic trend of 0.07 C per decade would give you: 100 years times 0.07 C per 10 years=0.7 C. The observed total 150 year linear trend and our deduced anthropogenic trend fitted to a linear trend is also the same. There is no controversy about the 100 year or the 150 year linear trends. Note that the deduced anthropogenic response in our paper is the regressed trend (using whatever the placeholder is in the intermediate step, which could be linear or QCO2) plus the residual, the latter also has a trend. We called this the adjusted data, which is the original observation minus the influence of ENSO, solar, volcano and AMO. This adjusted data has a nonlinear trend. If you know what the true anthropogenic response is, it is this adjusted data (I think it is your greenline) that you should be comparing with the true data (I think it is your red line). In our paper, we have, to aid visualization, used 150-year, 100-year, 75-year, 50-year and 33-year linear trends to demonstrate that while in the total observed temperature there is an acceleration of trends depending on the interval taken to measure the linear trends, such acceleration has been much reduced for the past 100 years once the AMO and other natural influences have been removed. The statistical comparison between the true value and the adjusted data is what one should be focused on and I will do that in my rebuttal. I think by now I understand what Dikran's intent was.
Tung&Zhou 2013 concludes its abstract as follows -"The underlying net anthropogenic warming rate in the industrial era is found to have been steady since 1910 at 0.07–0.08 °C/decade, with superimposed AMO-related ups and downs that included the early 20th century warming, the cooling of the 1960s and 1970s, the accelerated warming of the 1980s and 1990s, and the recent slowing of the warming rates. Quantitatively, the recurrent multidecadal internal variabil ity, often underestimated in attribution studies, accounts for 40% of the observed recent 50-y warming trend." (My emphasis)
I pointed out @148 above both that half the HadCRUT4 signal remained even after the MLR had been performed and that the "recent slowing of the warming rates" were unchanged when the anthropogenic warming was represented by the QCO2(t) function as presented in Figure 3 of the first part of this post. I was wrong in this last part of my statement. Closer analysis of Figure 2b in the first post (Figure 5b of T&Zh13) shows the temperature record when Sloar, ENSO, Volcanic & AMO signals are accounted for and this clearly demonstrates that the "recent slowing of the warming rates" have indeed changed. The recent slowing has been slowed even more by the performance of the MLR. Also the HadCRUT signal remains essentually unaltered.
I would like to point out that Prof. Tung has yet again failed to answer a direct question. It is unsurprising that I had to keep updating my example in order to address Prof. Tungs' repeated misunderstandings, that is the way scientific discussions normally proceed. Had Prof. Tung answered the questions I posed to him, we may actually have reached understanding at some point. However if we have reached the point where it cannot even be freely acknowledged that a value lies outside a confidence interval, I don't see that there is any likelihood of productive discussion.
It has occurred to me that the most neutral definition of the AMO would be the unforced variation in North Atlantic SST. Given that forcing from aerosols is regionally confined, the forcing in the North Atlantic can be expected to differ substantially from global forcing, given that aerosol emissions from North America and Europe have varied substantially with changes in dominant fuel use, wars and emissions controls. Therefore, the least question beging approach to identifying the AMO in the twentieth century would be to determine the effect of NA forcing on NA SST by regression, then remove that influence mathematically. As water from the South Atlantic is fed into the Gulf Stream and hence influences NA SST, it may also be desirable to eliminate that influence by the same means. Having removed the influence of NA Forcings and SA SST from the NA SST, whatever remains would approximate to the unforced variation in SST. It may or may not contain a 70 year cycle of any significant magnitude.
I have two questions.
First, has anybody actually taken this approach and reported the results?
Second (specifically for KK Tung), if you identify the unforced SST variation in the NA by this means, and use that instead of your AMO in your multiple regression, what is the resulting anthropogenic trend?
Tom Curtis @168.
You most likely still do get a wobble from calculating NA SST - SA SST. The actual values would require delving into grided data but the NCDC provide SST for differing latitudes that I recently graphed. (Thus the N Atlantic & N Pacific SST are combined.) The wobble has a definite "limp" for 0-30ºN and an 'anti-limp' in the Arctic. If you assume the limp & anti-limp can be explained away without diminishing the AMO as a natural wobbler of global temperature, and noting there is no matching wobble for Southern SST, I think the maximum contribution from these SSTs into the average global figure is about the same for both wobbles (the Arctic being smaller than the Northern tropics) at 0.065ºC peak-to-peak. T&Zh13 suggests a far higher figure: 40% of recent warming = 0.265ºC peak-to-peak.
With the HadCRUT4 profile evident interannually on the T&ZH13 MLR results in Fig 5b, it eventually dawned on me that it was odd the same profile wasn't evident in fig 5a. So I did a quick scale of that graph and for comparison also the HadCRUT3 results from Foster & Rahmstorf 2011.
So why does the introduction of AMO into the MLR re-introduce HadCRUT4 wobbles? Is it the Sol, Vol & ENSO signals in AMO cancelling out their input into the analysis?
In reply to Dikran Marsurpial in his post 167: I do not appreciate your misleading statement of the facts.
I would like to point out that Prof. Tung has yet again failed to answer a direct question. It is unsurprising that I had to keep updating my example in order to address Prof. Tungs' repeated misunderstandings, that is the way scientific discussions normally proceed. Had Prof. Tung answered the questions I posed to him, we may actually have reached understanding at some point. However if we have reached the point where it cannot even be freely acknowledged that a value lies outside a confidence interval, I don't see that there is any likelihood of productive discussion.
Let me review the facts, and you can see that I have been very patient with you out of respect. Your above statement shows that you do not treat me with the same respect.
(1) I replied directly in my post 120 to your post 115, where an original example was created in post 57 that supposedly has demonstrated an inaccuracy in the multiple linear regression (MLR) estimate of the hypothetical anthropogenic warming. I missed that thread, which was after the part 1 of my originally post. You and Dumb Scientist pointed this out to me in the comments on part 2. At the time you also said: “It is rather disappointing that you did not give a direct answer to this simple question”, referring to the question: “Is there an error in my implementation of the MLR method? Yes or No”. Your implementation was correct but you neglected to give error bars. We repeated your example and gave the error bars and showed the MLR method correctly gave the true answer in the example within the 95% confidence level. Your case was completely demolished. How much more direct do you want? Of course I did not use those words out of courtesy.
(2) Your “updating of my example” was not done to address my “repeated misunderstanding”, but was done to salvage the example mentioned in (1) that I had directly responded---the true value does lie within the confidence level--- and thought we had concluded . There was no misunderstanding on my part. You did not have to “update” your example.
(3) In your post 123, you updated your original example by saying “I am no longer confident that my MATLAB programs actually do repeat the analysis in the JAS paper…” You did this in lieu of agreeing with me and admitting that your original conclusion that the true value lies outside the confidence level was incorrect. If you had agreed we could have brought this episode to a conclusion. Instead you created a new example without an AMO in your data, and supposedly showed that the MLR found an AMO. I addressed directly this new example by pointing out the logical fallacy in your argument: just by assigning the name AMO to the MLR regressor does not mean that you told the MLR procedure what you had in mind for the AMO. I said: “It appears that your entire case hinges on a misidentified word.”
(4) In your post 134, you finally admitted your logical error, at least that was what I thought: You said: “OK, for the moment let’s forget about AMO and concentrate on the technical limitation of MLR…”. With this you created another new example.
(5) I suspected there was something wrong with the new example, It probably was not what you intended. Instead of blasting you, I gave you the benefit of doubt by asking you a few questions in my post 150, in particular whether there was a typo. After a while I posted in post 154 my direct response and again demolished your example. However, it turns out that there was indeed a typo and you had responded by saying so in your post 151. Post 151 started on a new page, and I saw it only after I posted my post 154. So my effort in addressing an example with an honest typo was wasted.
(6) Even correcting the typo, there was an error in the plotting (in offsetting), which supposedly showed that the true value lies above the deduced anthropogenic response plus noise. I pointed this error out. The true value lies above the deduced value only because the deduced value is offset to have zero mean while the true value has a positive mean. But you refused to acknowledge the error and thought it was “irrelevant”. Nevertheless you did replot your figure in post 158. That figure now shows that the true value for anthropogenic response, the red line, lies within the deduced anthropogenic response plus residue, the green curve.
(7) This now brings us to where we are now. I will say in the next post explicitly what is wrong with this example.
In reply to Dikran Marsupial in his post 167:
I was trying to give you the benefit of doubt and tried to clarify with you about what you really meant first before criticizing your example. You thought I was avoiding your direct question. Let me be more direct then. You focused on the wrong quantity, the blue line, while you should be focusing on the "adjusted data", the green curve. And yes, the true value lies within the 95% confidence interval of the deduced result.
I understand the intent of your thought experiment: If an index to be used for the AMO is contaminated by other signal, such as the nonlinear part of the anthropogenic response, the anthropogenic signal deduced using MLR with such a contaminated index as a regressor may underestimate (or overestimate) the true value, i.e. the true value may lie outside the confidence interval of the estimate. While this remains a theoretical possibility, and I have said many times here that we should always be on guard for such a possibility, your example has not demonstrated it. You have not come up with a credible example so far, despite many tries.
I have discussed extensively on how the adjusted data is obtained in part 1 of my post and its interpretation as our best estimate of the "true anthropogenic warming" ---the phrase used by Foster and Rahmstorf (2011). The adjusted data includes the residual and should include the anthropogenic response. One can fit linear trends to segments of it for visualization. Both Foster and Rahmstorf and we in our papers focus on the recent decades (the past 32 years since 1979, when satellite data became available), when the anthropogenic warming was thought to be accelerating. It was the low value of the 32-year trend that we published that has been the topic of debate here at Skeptical Science. The observed global mean temperate warmed at about twice the rate we deduced for anthropogenic response for the past 32 years.
We have performed 10,000 Monte Carlo simulation of your case. Here are the results:
(1) Without changing anything in your example except correcting the typo:
You did only one realization, and the corrected result was shown in the Figure on post 158. The true anthropogenic signal is the red curve (labeled A), and the MLR estimate is the green curve, which was labeled as “deduced A+residual”. It is seen that for this one realization, the true value lies within the green curve. So the direct answer to your question is: No, the true value does not lie outside the confidence level.
Let us focus on the last 32 years, and fit a linear trend to the green curve and compare that with the linear trend of the true A. By repeating it 10, 000 times each time with a different realization of the random noise, we find that the true A linear trend, which is 0.054 C per decade, lies within the 95% confidence interval of the MLR estimate over 70% of the time.
There are some problems with your implementation of the MLR procedure. These, when corrected, will increase it to over 90% the times when the true value lies within the confidence interval of the estimate. I will discuss these in the following.
(2) Incorrect implementation of MLR: Using two regressors for the same phenomenon:
Let Y be the observation: In your construction it consists of an anthropogenic signal, which is quadratic:
A=0.00002*(T+T^2),
and a natural oscillation with a 150-year period:
B=0.1*sin(2*pi*T/150).
In addition there is a random noise =0.1*randn(size(Y)), and a deterministic noise with 81-year period:
D=0.05*sin(3.7*pi*T/150).
You called D, the “unobserved signal”. There is no such thing as an unobserved signal (see (3) below). I see it as your attempt to introduce a “contamination”, in other words, noise, without accounting for it in the amplitude of the noise term. Let us not deal with this problem here for the moment. Your Y is:
Y=A+B+D+randn(siz(T)).
You next want to create a regressor C, but assume that the data available to you is contaminated by D and by the quadratic part of A. There is no random noise contamination.
C=D+0.5*A+0.5*B.
The linearly detrended version of C is denoted by Cd.
You then performed a MLR using three regressors, a linear trend, Cd and B. You did not say what Cd is a regressor for. I will consider two cases: First, it is a contaminated regressor for B, or second it is a regressor for the “unobserved” signal D. If it is a regressor for B, then having both Cd and the perfect regressor B for B is redundant. The reason is as follows: If you already know the perfect regressor for B, why use a contaminated regressor for it as well? If you do not know the perfect regressor for B, and must use the contaminated regressor Cd, then in the MLR the regressors should be two: the linear trend and Cd, with B deleted.
We performed 10,000 Monte Carlo simulation of the MLR of the problem as posed by you, but used two instead of the three regressors (B is deleted as a regressor, but it remains in the data). The true A value lies within the 95% confidence interval of the estimated 32-year trends 90% of the time if the linear trend is used as a placeholder in the intermediate step, and 94% of the time if the QCO2 regressor is used as a placeholder in the intermediate step of the MLR.
(3) There is no such thing as an unobserved signal:
D, being a perfect sinusoid with 81 year period, is directly observable using Fourier methods, in particular the wavelet method we used in our PNAS paper. Using the wavelet or Fourier series method we can separate out D and B to yield A within the 95% confidence interval over 99% of the time.
If the “unobserved” signal D is a signal of interest, such as the AMO, but that it is contaminated by B and A, then you are correct in using three regressors, the linear trend, Cd and B. I would suggest in that case that you first regress out the B signal in C before using it as your regressor for D. This method was discussed in our paper, Tung and Zhou (2010), JAS, called nested MLR.
In conclusion, you have not come up with an example that demonstrates that a contaminated index may cause the estimate of the true value to differ from the true value beyond the confidence interval. By this time you must have learned that it is very difficult to come up with such an example, despite some of the extreme cases that you have tried. If you wish to change your example again please understand that you are not doing it because you are addressing the “repeated understandings” from me.
Prof. Tung wrote: "There is no such thing as an unobserved signal:"
This again shows that you still do not fully grasp the problem. There clearly is an unobserved signal, which represents the true behaviour of the AMO. The AMO that is observed is contaminated by both anthropogenic and natural forcings. There is no way to recover the true AMO signal unless you know what effect anthropogenic forcings and natural forcings have on the true AMO signal, or you knew what the true AMO signal looks like a-priori. Now if you do know what the true signal actually looks like, there would be no need (and indeed no point) in linearly detrending the AMO signal.
Sadly the last line of your post is a good indication why this discussion is likely to be fruitless:
"If you wish to change your example again please understand that you are not doing it because you are addressing the “repeated understandings” from me."
The one thing that is almost guaranteed to prevent a misunderstanding from being resolved is for one party to be unable to accept that they may have misunderstood something (how could they possibly know anyway!). I can assure you that you still have not grasped a key point, which is that there undoubtedly is an unobserved signal. The existence of several recent journal papers discussing how to remove the contamination clearly demonstrates that we do not know what the true AMO signal (D) looks like - hence it is unobserved.
Regarding the statement "There is no such thing as an unobserved signal:"
There is a context in which this is true: any observation is a response to everything that affects it, so any signal that is relevant is part of the observation. That is just a tautology, though, and is about as useful as saying "all models are wrong" without completing the quote with "but some models are useful".
You could also say, just as easily, that all observations are wrong - but some observations are useful. All observations are a response to a variety of things, and the trick is to try to make observations that are strongly dependent on the thing that you are interested in, and only weakly dependent on (or independent of) things that you aren't interested in. Traditionally, when observations are partly dependent on things we aren't interested in, we consider those other factors to be sources of error.
An "unobserved signal" can be a factor that you've missed, that is affecting the observations that you are making, but you don't realize it. You think that your observation is a measure of A, but it is actually affected by other, non-observed factors. That factor is in the main observation, but is being missed ("unobserved") in the analysis and interpretation (and conclusions).
All of this discussion runs circles around a couple of issues where this is fundamental:
a) how much of the global temperature signal is due to anthropogenic causes?
b) what is AMO and what does it tell as about a)? In other wrods, what is it that AMO depends on, and to what extend do global temperatures depend on AMO?
We know a few things:
1) AMO is not an observation - it is a derived quantity based on a rather large number of observations.
2) AMO is at least partly derived from temperatures, and needs to be detrended. There are many ways to do this, yielding similar but not identical results. In order for AMO to not be dependent on long-term temperature trends, this detrending must be completely accurate. If it is not completely accurate, then AMO will still have some dependence on that trend - there will be a source of error.
3) Because there are many flavours of AMO, is is clear that AMO in any single incarnation is partly dependent on what AMO is supposed to mean (pick whatever you want), but also partly dependent on other factors. We know that all of them can't be perfect - and we don't really expect that any single one will be perfect. Thus, any AMO index is an imperfect representation of whatever AMO is supposed to be "for real".
4) When AMO is used as part of the explanation of global temperature trends - and then as justification for a conclusion that anthropogenic influences are small - then you'd better be pretty darn sure that you know exactly what it is that your AMO derivation represents. In particular, you'd better be pretty darn sure that your AMO numbers aren't partly dependent on the thing that you think you are using AMO to explain.
Now, I havrn't attempted to duplicate everyones' math here, but this is what I see so far:
i) Item 4 risks circular reasoning in a sort of feedback loop: AMO affects global T, which affects the temperatures that AMO is derived from, which may affect AMO if detrending is done incorrectly. I am not at all convinced by what Dr. Tung has written here in defence of his processing, interpretations, and conclusions.
ii) Dikran has provided a thought experiment, which attempts to apply Dr. Tung's methodology to a set of numbers derived from a known/defined mathematical construction - i.e., a dataset where the answer is known in advance.
iii) Dikran's example shows that Dr. Tung's methodology fails to come up with the correct answer (which was known because Dikran created it). The numbers don't actually have to mean anything at all - this is strictly a mathematical exercise, and the numbers could be anything, from temperatures to Starbuck's coffee sales. The fact that the mathematical methodology fails to reproduce the answer that was used to derive the example is a serious issue. In mathematical proofs, this would be reductio ad absurdum: assume one thing, and come up with a result that is contrary to that assumption, then either the assumption is false, or the methodology is false. Dr. Tung's assumption is that he has properly broken the circular reasoning mentioned in #4, whereas other disagree. Dr. Tung has criticised Dikran's choice of labels, but in mathematics, labels (AKA variable names) are irrelevant - it is the relationships that matter. Dr. Tungs' focus on what the labels are supposed to mean may be why he has such a problem seeing the mathematical errors in his methodology.
iv) From my reading, Dr. Tung has failed to justify why his methodology will give the right answer in his case, when we know that the methodology fails in Dikran's example. Dr. Tung has said the thought experiment is not realistic, but the numbers don't have to have anything to do with reality - mathematics that can't reproduce themselves don't get better when fed with "real" numbers instead of made up numbers. Correct mathematics works on purely mathematical grounds, without reference to any outside idea of "reality". [Mathematics becomes useful, and of interest to non-mathemeticians, when we can relate it to reality, but mathematics doesn't need it.]
So, from my humble viewpoint, Dr. Tung's work is seriously flawed, as demonstrated here by others. HIs methodology can't answer itself, and much of his argument is just a reassertion of his views.
In reply to Dikran Marsupial in his post 173: For someone who has been so picky about the use of words, you should state clearly that you have extraneous meaning to the word "unobservable signal". You defined your "unobservable signal D" as a sinusoide with a period of 81 years. You did not call it AMO, nor have you attributed physical interpretations to it. You wanted me to address directly the questions that you posted as you posted it. This signal D is in your Y, which you intended it to be an observation. I can observe your D in Y by doing a Fourier spectrum. There is no such thing as an unobserved signal in this context. You did not ask for a physical interpretation of the signal D, whether it is forced or natural. Even in the "contaminated signal" C, I can recover your "unobserved signal D" by Fourier spectrum, so it is not "unobservable". I stated clearly why I said it is not "unobservable". For someone who is so picky about the use of words, perhaps you should define what you mean by "unobservable". Please note that in your example that I was responding to, the phenomenon AMO was never mentioned, nor what is forced and what is natural.
In reply to Bob Loblaw in post 174:
How did you come to the conclusion "iii) Dikran's example shows that Dr. Tung's methodology fails to come up with the correct answer (which was known because Dikran created it)." ? I thought we just showed in my post 172 that it was incorrect for him to draw that conclusion. If you have evidence that Dikran's example shows that our methodology fails to come up with the correct answer, please point it out to me.
Please take a look at his figure in Dikran's post 158, the true A in red is entirely within the estimate, in green. I tried to be even more conservative than Dikran, and say this successful estimate is only one realization. We went on to look at 10,000 realizations, and found that this success occurs 70% of time. This is using his convoluted example unchanged. When we cleared up some of the convolution the success rate goes above 90%. Given this, how did you still come to the conclusion that his example showed that our methodology failed?
Prof Tung@175 As it happens I was using the word "unobservable" is its usual everyday meaning, i.e. "not accessible to direct observation". If the meaning were not clear to you, a better approach would be to ask what it meant, rather than make an incorrect assumption leading to yet another misunderstanding.
The physical process of AMO is not (currently) accessible to direct observation, instead it is deduced from Atlantic SSTs. Therefore in my thought experiment I said that D was unobservable to parallel the fact that we don't observe the true AMO. Trying to get round this restriction by Fourier analysis is clearly just violating the purpose of the thought experiment rather than engaging with it.
Prof. Tung@176 writes "Please take a look at his figure in Dikran's post 158, the true A in red is entirely within the estimate, in green."
The green is not the estimate, as I have already pointed out, the confidence interval on the regression coefficient is, and the true value is not within it.
I have already pointed out that the offset on the green signal is arbitrary and essentially meaningless. It is common statistical practice to subtract the means from variables before performing the regression, in which case the red curve is not in the spread of the green signal anyway. That is what I did the first time. For the second graph I changed the offset at Prof. Tungs request, to show that it made no difference to whether the true value was in the confidence interval or not.
In this case, we are looking at the time variable T. Should it make a difference to the result if we start measuring time from 0AD or 1969 or 1683 or 42BC? No, of course not, the point where we start measuring time is arbitrary (unless perhaps we use the date of the big bang). Thus it is perfectly reasonable to center (subtract the mean from) the time variable, as I did.
In Reply to Dumb Scientist’s post 153: We applaud Dumb Scientist for grounding your example with aspects of the real observation. By doing so you have come up with the first credible challenge to our methodology. Our criticism of your original example was mainly that the noise in your N. Atlantic data was the same as the noise in the global mean data. In fact, they came from the realization. This is extremely unrealistic, because the year-to-year wiggles in N. Atlantic line up with those in the global mean. Much of the year-to-year regional variations come from redistribution or transport of heat from one region to the other in the real case, and these are averaged out in the global mean. We argued in our PNAS paper that it is the low-frequency component of the regional variability that has an effect on the global mean. So although you tried to match the high correlation of the two quantities in the observed, this was accomplished by the wrong frequency part of the variance. In my post 124 I offered two remedies to the problem of the noise being almost the same in your example in post 117: (1) increase the regional noise from 0.1 to 0.3. This created a difference of the N. Atlantic data from the global mean data. Here you said you do not like this modification because it is making the variance too large. (2) Keep the noise amplitudes the same as what you proposed, but the noise from the regional data is from a different draw of the random number generator than the noise from the global mean. If you agree with the amplitudes of the noise in your previous example, then we can proceed with this example. Your only concern in this case was that the correlation coefficient between N. Atlantic and global data is 0.64, a bit smaller than the observed case of 0.79. “That looked more realistic but the average correlation coefficient over 10,000 runs was 0.64±0.08, which is too small.” I suggest that we do not worry about this small difference. Your attempt to match them using the wrong part of the frequency makes the example even less realistic. We performed 10,000 Monte- Carlo simulations of your example, and found that the true value of anthropogenic response, 0.17 C per decade, lies within the 95% confidence interval of the MLR estimate 94% of the time. So the MLR is successful in this example. If you do not believe our numbers you can perform the calculation yourself to verify. If you agree with our result please say so, so that we can bring that discussion to a close, before we move to a new example. Lack of closure is what confuses our readers.
You casually dismissed the wavelet method as “curve-fit”. Wavelet analysis is an standard method for data analysis. In fact most empirical methods in data analysis can be “criticized” as “curve-fit”. The MLR method that you spent so much of your time on is a least-square best fit method. So it is also "curve-fit". For your examples and all the cases discussed so far, the estimation of the true anthropogenic response by the wavelet method is successful. When in doubt we should always try to use multiple methods to verify the result.
In post 153, you created yet a new example. This example is even more extreme in that the true anthropogenic warming is a seventh order polynomial, from the fifth order polynomial in your original example in post 117, and the second order polynomial in Dikran Marsupial’s examples. This is unrealistic since in this example most of the anthropogenic warming since 1850 occurs post 1979. Before that it is flat. This cannot be justified even if we take all of the observed increase in temperature as anthropogenically forced. It also increases faster than the known rates of increase of the greenhouse gases. You decreased the standard deviation of the global noise of your original example by half. You took my advice to have a different draw of the random number generator for n_atlantic but you reduced the variance from your original example.
From your first sentence: "My Monte Carlo histograms estimated the confidence intervals", we can infer that you must have used a wrong confidence interval (CI). We have not realized that you have been using a wrong CI until now. The real observation is one realization and it is the real observation that Tung and Zhou (2013) applied the multiple linear regression (MLR) to. There is no possibility of having 10,000 such parallel real observations for you to build a histogram and estimate your confidence interval! So the CI that we were talking about must be different, and it must be applicable to a single realization. Our MLR methodology involves using a single realization to first coming up with the “adjusted data”, which is obtained by adding back the residual to the regressed anthropogenic response, as discussed in part 1 of my post. The adjusted data can be interpreted as anthropogenic response with climate noise. If the procedure is successful the deduced adjusted data should contain the real anthropogenic response. For the hypothetical case where you know the true anthropogenic response, one needs to have a metric for comparing the adjusted data, which is wiggly, with the true value, which is smooth. One way for such comparisons is to fit a linear trend to a segment of the adjusted data and compare such a trend with the corresponding trend of the true anthropogenic response. The segment chosen is usually the last 33 years or the last 50 years. In fitting such a linear trend using least squares fit we obtain a central value (or called the mean) and deviations from the mean. The two standard deviations from the mean constitute the confidence interval (CI) of that estimate. If the true value lies within the CI of the estimate, we say the estimate is correct at 95% confidence level. This is done for each realization. When there are many more realizations, we can say how many times the estimate is correct at 95% confidence level.
Continue from my post 178: Given your new example, which I think is unrealistic in the shape of the total global mean temperature not having any trend before 1979 and most of the trend occurring after, I would not have chosen to have a linear function as a first guess in the multiple linear regression procedure. I would choose a monotonic function that looks like the the total trend as a first guess, such as QCO2 discussed in part 1 of my post.
Using your exact example and your exact method (with linear trend as a regressor for human), we repeated your experiment 10,000 times, and found that the true human answer lies within the 95% confidence level of the estimate 94% of the time. This is using the linearly detrended n_atlantic as the AMO index, unsmoothed as in your original example. If this AMO index is smoothed, the success rate drops to 33%. In our PNAS paper we used a smoothed AMO index and we also looked at the unsmoothed index (though not published), and in that realistic case there is only a small difference between the result obtained using the smooth index vs using the unsmoothed index. In your unrealistic case this rather severe sensitivity is a cause of alarm, and this is the time for you to try a different method, such as the wavelet method, for verification.
Actually, both of my simulations used the (nonlinear) exact human influence as a human regressor, specifically to avoid this objection. You can verify this by examining my code: "regression = lm(global~human_p+amo_p)". Since correcting this misconception might alter some of your claims, I'll wait to respond until you say otherwise.
Two corrections to my post 179:Using your exact example and your exact method (with linear trend as a regressor for human), we repeated your experiment 10,000 times, and found that the true human answer lies within the 95% confidence level of the estimate 94% of the time. There are two errors in this sentence of mine: 94% should be 93%, and the (....) should be deleted, because we were using the exact method of Dumb Scientist, who used the exact human regressor. DS also pointed out this second error on my part. Sorry. I wrote that post on a small laptop while traveling without checking/scrolling the posts carefully.
Sorry for the delay. I now think more than 10,000 Monte Carlo runs are necessary for stable statistics, but I'm traveling now and only have access to my netbook. When I return home next Monday I'll try 1,000,000 runs on my desktop and reply as soon as possible.
Thanks to Bob Loblaw for running this new R script on his computer.
Linear regression depends on the overall correlations, so a realistic simulation will match that rather than trying to match the correlations at specific frequencies. After you criticized my original simulation's high correlation coefficient, I chose new parameters so the synthetic correlation was slightly below the real value. The low-frequency component of my synthetic N. Atlantic SST already affects the global mean because the 70-year "nature" sinusoid is present in both timeseries.
Let's judge realism by first considering the real timeseries:
In contrast, here are synthetic timeseries using Dr. Tung's preferred parameters:
Now here are synthetic timeseries using my preferred parameters:
Your claim that my new example is "even less realistic" is completely unsupported. I suggest that we do worry about this "small difference" between the correlation coefficients of your suggested timeseries vs. those of the real timeseries because MLR is based on correlations, and your suggested timeseries' correlation coefficient is so low that the real value doesn't even lie within its 95% confidence interval.
For your preferred parameters, I actually find an even higher success rate. This shouldn't be surprising, because your correlation coefficient is much lower than the real value, which causes the regression to underweight the AMO and thus increases the estimated trend. Your timeseries also have variances that are much larger than the real values, which inflates the uncertainties. Here's a boxplot of your post-1979 trend uncertainties vs. the trends:
The comparable white-noise uncertainty for real data is 0.034°C/decade, which is much smaller than your synthetic uncertainties. If you increase the variances even higher above the real variances, the uncertainties will be so large that you'll be able to claim 100% success. But that wouldn't mean anything, and neither does your current claim.
My original simulation's Monte Carlo histograms estimated the confidence intervals. For comparison, my second simulation also calculated 95% confidence intervals around each realization; these came from the least squares fit using the standard procedure you descibed. Here's a boxplot of my post-1979 trend uncertainties vs. the trends:
The comparable white-noise uncertainty for real data is 0.034°C/decade, which lies within my synthetic uncertainties. The true post-1979 trend lies within the 95% confidence interval only 9% of the time, but this statement doesn't report the best-fit trend or the uncertainties so I think the boxplots and histograms are more informative.
As discussed above, these new parameters were chosen to address your concerns about the correlation coefficients and variances of the real vs. synthetic time series. The exponents were chosen so the true post-1979 anthropogenic trend is 0.17°C/decade in both cases.
These are thought experiments, which eliminate real-world complications to focus on the key issue. I'm not suggesting that the real human influence is a 5th or 7th order polynomial. But if your method can detect nonlinear AGW, it should recover the true post-1979 trend in these hypothetical cases.
It's strange that you're disputing the shape of my thought experiment's total human influence. We can easily measure the variances and correlations of the real timeseries (and my preferred synthetic timeseries match better than yours), but you've pointed out that aerosols are uncertain so we can't easily measure the total human radiative forcing. Also, the total human influence on temperature is roughly proportional to the time integral of these total human radiative forcings, so it should grow faster than the forcings.
As you note, I already addressed this criticism by drawing global and regional noises from different realizations. But even in my original example, the N. Atlantic noise wasn't the same as the global noise because the N. Atlantic data had extra regional noise added to the global noise.
Again, my case is more realistic than yours in terms of timeseries appearance, correlation, variances, and error bars. Ironically, I think my case is more sensitive to smoothing than yours because I took your advice to make the regional noise proportionally larger compared to the global noise. Your global noise (0.2°C) is twice as large as your regional noise (0.1°C) but mine are both equal to 0.11°C, so smoothing my AMO index removes proportionally more uncorrelated noise than smoothing yours. I tested this by setting "custom" parameters equal to mine (with my 7th order human influence, etc.) but with your noise parameters, and observed similar sensitivity to smoothing the AMO index over 10,000 runs.
Indeed, that's why I don't think wavelets are different enough from linear regression to provide independent methodological support. Again, attribution is really a thermodynamics problem that needs to be calculated in terms of energy, not curve-fitting temperature timeseries. Your curve-fitting claim that ~40% of the surface warming over the last 50 years can be attributed to a single mode of internal variability contradicts Isaac Held and Huber and Knutti 2012 who used thermodynamics to conclude that all modes of internal variability couldn't be responsible for more than about 25% of this surface warming.
I set "custom" parameters equal to mine (with my 7th order human influence, etc.) but with Dr. Tung's noise parameters, and 10,000 runs seemed to show that the sensitivity to smoothing was similar to simulations using Dr. Tung's overall parameters. This would have suggested that my simulation's sensitivity to smoothing the AMO index was related to the relative noise levels. However, running 100,000 simulations of the custom parameters reveals sensitivity similar to my overall parameters, so my hypothesis was wrong.
I still don't know why my simulation is more sensitive to smoothing, but I think the important point is still that my parameters produce more realistic timeseries, correlations, variances, and error bars. (Also, attribution is still really a thermodynamics problem.)
Our exchanges on analysis procedures of a technical nature probably have left most of our readers confused. So let me summarize the major points under debate. Both Dumb Scientist (DS) and Dikran Marsupial have focused on the technical aspects of the Multiple Linear Regression analysis (MLR). This was one of the three data analysis methods that were used on the problem with the aim of deducing the secular trend after removing the oscillatory influence of Atlantic Multi-decadal Oscillation (AMO). Our PNAS paper used two methods, the MLR and the wavelet analysis, and obtained approximately the same result. Previously, Wu et al (2011, Climate Dynamics) used the method of Empirical Mode Decomposition (EMD) and obtained similar results. The EMD method was relatively new, and there were questions on whether other, more commonly used methods could yield the same result. Our PNAS paper was in part (though a small part) trying to reproduce their results using two other methods. The larger aim of our PNAS paper was to argue that the AMO is mostly natural.
Two technical aspects of the MLR have been debated here. Dikran chose to focus on our use of a linear regressor as a placeholder in an intermediate step of the MLR process. This issue was discussed in part 1 of my post, and shown that when the residual is added back as in the published papers (Foster and Rahmstorf (2011), Zhou and Tung (2013), Tung and Zhou (2013)), the sensitivity to the particular intermediate step is greatly reduced. While Dikran may disagree with my summary, I think he has failed to come up with an example where our procedure fails to yield the right answer within the 95% confidence interval (CI) most of the time. Please see my posts 171 and 172 for a summary.
Although I had originally thought that Dumb Scientist also focused on our use of linear regressor as the reason for his assertion that our argument was circular, he later clarified that his focus was on how the definition of the AMO index from the North Atlantic temperature affects the deduced anthropogenic trend. This is a more worthwhile challenge. My collaborator Dr. Zhou and I were interested to follow this debate to find out under what condition the MLR procedure would fail. After all, no empirical method is expected to work under all conditions. So we thank DS for his efforts.
His sequence of examples has evolved into the following: Consider a hypothetical example where we know what the true answer is, and make such an example as realistic as possible (with respect to the correlation between the global mean data and the N. Atlantic data, and the variances in each) so that if the MLR procedure fails in this hypothetical case it is likely to fail in the real case also. The observed temperature (HadCRUT4) warms at the rate of 0.17 C per decade after 1979. This was proposed previously by Foster and Rahmstorf (2011) as the “true anthropogenic trend”. Tung and Zhou (2013), on the other hand, argued that this observed rate of warming includes the rising half cycle of the AMO, which when removed, would yield an anthropogenic trend that is approximately half as large. So the question is, what if the true anthropogenic warming trend is actually 0.17 C per decade in a hypothetical example, will the MLR procedure erroneously say that it is smaller? While I have always maintained that such a theoretical possibility exists, it has been surprisingly difficult to actually come up with an example where MLR fails, and we collectively have gone through examples where the hypothesized anthropogenic warming goes from quadratic to a fifth order polynomial. The example that DS finally came up with consists of a 7th order polynomial for the anthropogenic trend (called human). It has the property that it is warming at 0.17 C per decade post 1979, but no warming before that. The latter fact is unrealistic but necessarily follows from the high order polynomial form assumed for this anthropogenic warming if one uses only analytic forms. There is in addition a 70-year oscillation, which is the AMO (called nature by DS). The global mean temperature is assumed to consist of human + nature + random noise. The N. Atlantic temperature that is used to define an AMO index also consists of these three components but in different proportions. The AMO Index is obtained by linearly detrending the N. Atlantic temperature. The idea is that because the anthopogenic trend is highly nonlinear, linearly detrending the N. Atlantic temperature yields an AMO contaminated by the nonlinear part of the anthropogenic trend. Therefore, if this “AMO” is removed by the MLR procedure, what remains is a more linear trend that is an underestimate of the true nonlinear anthropogenic trend. At least that is the aim of DS, as I understand it.
MLR can fail if the two components that we try to separate (in this case, the AMO and the nonlinear anthropogenic trend) have approximately the same scale, about 35 years, as is the case with DS’s latest example with the high order polynomial. Although the MLR method still can yield the right answer within the 95% CI most of the time (see my posts 178 and 179), it is nevertheless showing symptoms of non-robustness, e.g. sensitivity to the choice of regressors (smoothed vs non smoothed), which neither DS nor we understand at the moment, and we don't have the time to investigate it deeper. In the real case considered in our papers, such sensitivity does not exist and we got approximately the same answer. However, this example is not relevant, despite efforts by DS to make it realistic in other aspects, because we know, based on our current understanding of greenhouse warming, that there has been a warming since 1900. So the time scale for the anthropogenic warming is not 35 years but over 100 years.
The following example remedies this one deficiency in the example by DS that makes his case study less relevant. That is, we still use the hypothesis, as DS did, that the true post-1979 warming is entirely anthropogenic, and so the true human warming rate is 0.17 C per decade. Before that time there is a gentler warming, which is equal to the smoothed secular trend in the observed warming from 1850 to 1979. Everything else remains the same as in DS’s example. We perform 10,000 Monte-Carlo simulations using his method for the MLR. (We think 10,000 is sufficient; there is no need for 100,000 Monte-Carlo simulations.) The MLR procedure obtains the correct answer, defined as within the 95% CI of 0.17 C per decade for the post 1979 trend, most of the time. Specifically, we obtain the correct answer 80% of the time if we use the linear regressor in the intermediate step, 95% of the time correct if we use the QCO2 as the regressor in the intermediate step, and 91% of the time correct if we use human as the regressor, as DS did. Therefore, regardless of the intermediate steps, the MLR is able to successfully separate the components to obtain the “true” answer. The reason that this time the MLR is able to separate the two components is because the anthropogenic warming and the AMO have different time scales, as they should in the real case.
Some details of how we came up with the hypothetical anthropogenic warming follow. As did DS, we tried to be consistent with observation. We start with the HadCRUT4 surface temperature data. We fit it with a 6th order polynomial over the entire period of 1850-2011, instead of just over the period 1979-2011 as DS did. This produces the observed 0.17 C per decade of warming after 1979, the same as in DS. But in contrast, the warming here exists over the entire period, not just after 1979. The polynomial is smoothed by a cubic spline so that the trend is monotonic before 1979. This anthropogenic component will be called human. It is denoted by the red curve in Figure a. To create the AMO the-above-obtained human is subtracted from HadRUT4 data. The difference is smoothed with a 50-90 year wavelet band pass filter. This is the AMO (note: not the AMO Index). This is called nature (denoted by the purple curve in Figure b) and is the counterpart to DS’s 70-year sinusoid.
The global data consists of these two components plus a random noise of standard deviation of 0.1. The AMO Index is created using the N. Atlantic temperature, linearly detrended. For the N. Atlantic temperature, we assume it is composed of an anthropogenic warming given by 0.8*human (since the observed long-term trend in the N. Atlantic is smaller than that in the global mean) and the natural component is 1.4*nature (since the AMO in the N. Atlantic is known to be larger than that in the global mean). The correlation coefficient between the global data and the N. Atlantic data in this synthetic example is 0.74+/-0.06, very close to the observed correlation of 0.79. There is in addition a random noise in the N. Atlantic with standard deviation of 0.15. The synthetic global variance is 0.071+/-0.008 and the synthetic N. Atlantic variance is 0.066+/-0.011, very close to the real variances of 0.07 and 0.05, respectively.
In conclusion, it has been surprisingly difficult to come up with a synthetic data where the MLR method fails to yield the right answer most of the time. The latest example by DS comes closest, but has an unrealistic deficiency. In all the cases considered, none has failed both of our methods, the MLR and the wavelet method. These debates have served the purpose of strengthening our confidence in using these methods, and in the technical correctness of the results that we obtained in our PNAS paper using the two methods, although we should always be on guard for the possible failures of any method we use. It should be pointed out however that none of these technical discussions concerns the larger picture: whether the AMO is forced or natural.
I hope with this summary we can conclude the technical discussion on the MLR procedure, and can now move on to the other threads, such as the “thermodynamic argument”, which supposedly sets an upper limit on how large natural internal variability can be.
[RH] Fixed image width.
On the “thermodynamics argument”: Dumb Scientist has repeatedly touted the thermodynamic argument as putting an upper limit on internal variability:
"Again, attribution is really a thermodynamics problem that needs to be calculated in terms of energy, not curve-fitting temperature timeseries. Your curve-fitting claim that ~40% of the surface warming over the last 50 years can be attributed to a single mode of internal variability contradicts Isaac Held and Huber and Knutti 2012 who used thermodynamics to conclude that all modes of internal variability couldn't be responsible for more than about 25% of this surface warming."
First, attribution is not necessarily a thermodynamics problem. The method adopted by IPCC AR4, the “optimal fingerprint detection and attribution method”. “is based on a regression of the observation onto model simulated patterns and relies on the spatio-temporal response patterns from different forcings being clearly distinct…..The global energy budget is not necessarily conserved and observed changes in the energy budget are not considered”. This quote came from Huber and Knutti, 2012.
Secondly, none of the published work could put such a tight upper bond on the contribution by internal variability. Huber and Knutti (2010) in Nature Geoscience, mainly used a zonal mean energy balance model of intermediate complexity, meaning a model without ocean dynamics. I believe this model has a diffusive ocean and therefore is not possible to have internal variability beyond a few months: “The energy balance model has no natural interannual variability but is able to reproduce the observed global trend of past temperature and ocean heat uptake”. The model’s ocean heat uptake is constrained using observation in the upper 700 meters: “Ocean heat uptake for 3000 m depth is also larger, but the model is only constrained using data to 700 m depth”. Given these uncertainties, which the authors acknowledged to be large, I would take the results to be a consistency test of models that have simulated the observed warming as almost entirely a response to forcing.
Towards the end of the paper, the authors compared the 50-year linear trends derived from unforced control runs in the CMIP3 models with the observed 50-year trends. These models do have internal ocean variability. ( DS, please note, this part is not based on a thermodynamic argument, but the result was what you referred to as from a thermodynamic argument.) The authors concluded “For global surface temperature it is extremely unlikely (<5% probability) that internal variability contributed more than 26+/-12% and 18+/-9% to the observed trends over the last 50 and 100 years, respectively”. So the “upper bound” is 38% for the last 50 years and 27% for the past 100 years, respectively. Given the uncertainty in the model’s oceans, I do not think these upper bounds rule out our ~40% and ~0% contribution of internal variability to the 50-year and 100-year trends, respectively.
On Isaac Held’s blog#16 that DS refers to as providing an upper bound of 25% for the contribution of internal variability to the surface warming for the past 50 years: We need to recognize that Held is using a very simple two-box ocean model to illustrate the process of energy balance that can be used to constrain the contribution from internal variability. The exact figure of 25% as the upper bound should not be taken too seriously, and it could easily be 40%, given the fact that there is at least a factor of two variation in climate sensitivity in the IPCC models and he picked one particular value of climate sensitivity from one of the GFDL models for illustrative purpose. There were many other simplifying assumptions so that an analytic result could be obtained. One of them is the assumption that ξ, the fraction of temperature change that is forced, remains constant in time as anthropogenic forcing increases. This would have required an increasing magnitude of internal variability. With this assumption, he was able to obtain the following formula:
Ocean heat uptake per unit forcing=Ocean heat uptake per unit forcing as if the entire temperature change were forced - (1-ξ)/ξ.
The last term is due to internal variability. It is negative, because ocean is supplying heat to the atmosphere to be radiated to space. Held estimated a typical value for the first term on the right-hand side to be ~0.3, from which he estimated that if ξ is smaller than 0.75 then the total ocean heat uptake would become negative. So the fraction of warming contributed by internal variability, (1-ξ), cannot be greater than 25% during a period when the ocean heat uptake is positive. This number can easily become ~40% if the forced response is slightly more efficient in storing heat in the ocean. Recent evidence of finding more and more of the forced warming in deeper and deeper ocean layers may suggest that the ocean is more efficient in storing heat than previously thought. Changing 0.3 to 0.5 would yield close to 40% for this upper bound.
KK Tung wrote " While Dikran may disagree with my summary, I think he has failed to come up with an example where our procedure fails to yield the right answer within the 95% confidence interval (CI) most of the time. "
This is simply incorrect. In the example here, the linear trend due to the anthropogenic component is estimated by the MLR procedure to be 0.0019 +/- 0.00039, the true value is 0.003, which is not in the 95% confidence interval. In this example, the MLR procedure underestimetes the anthropogenic component and the difference is statistically significant. Sadly there seems little point in continuing the discussion if this cannot be acknowledged and accepted, so I will leave it at that, so as not to distract from Prof. Tung's discussion with Dumb Scientist.
KK Tung.
I must admit to an error I made @170. The inter-annual wobbles from HadCRUT4 that I show on the graph linked @170 do not mysteriously feature on Tung&Zhou2013 Fig 5B. The data actually was scaled from Fig 2B from your first SkS post on this subject. I apologise for this error. (The appearance of the HadCRUT4 inter-annual wobbles in Fig 2B still remain unexplained but it is less 'mysterious' occurring on that graph than on Fig 5B.)
So I have double-checked and hope I make no error now, as I introduce another graph showing the data from Tung&Zhou2013 Figs 5A&B. It presents quite a few questions but I will kick off here by asking about the wobbles in the blue trace. This blue trace is the 10-year rolling average of residuals from the MLR obtained by subtracting the QCO2(t) function (introduced in your first SkS post) from the data presented in Fig 5B, and obviously re-based for clarity's sake.
According to Zhou &Tung 2013 which covers your MLR analysis more fully than T&Zh13 "The residual ... should only consist of climate noise if the MLR is successful..." This conforms to my understanding of it.
Yet the blue trace showing the residuals from the MLR analysis in Tung&Zhou2013 shows a lot more than "noise." There are distinct wobbles and these are not small wobbles being 43% that of the original HadCRUT4 wobbles (red trace). The reiduals thus contain a very significant part of the HadCRUT4 signal which the MLR analysis has failed to attribute.
A cynic would point to such wobbles within the residuals as being indicative of curve-fitting.
For myself, I am more charitable and rather see the problem being that these wobbles have gone unreported in Tung&Zhou2013. Indeed, a very similar trace can also be derived from Fig 1B Zhou&Tung2013 yet that paper says of the data in Fig 1B "The global-mean temperature adjusted this way shows mostly a monotonic trend with some scatter." This blue trace is definitely not "scatter."
(Note that the graph below features data derived from your Fig 5A&B in Tung&Zhou2013 as there are other feature beyond the blue trace that I see requiring explanation & which I hope we can address in later comments.)
Could you thus explain why this wobble is present in the residuals and why its presence has remained unreported?
Graph link
Thank you, MA Rodger, for your additional comments. I will take a look at this thread more carefully this weekend before replying.
In reply to MA Rodger at post 188: I had trouble understanding your original posts---that was the reason I didn't respond to them then. I may still not be understanding it; so please correct me if I misinterpret your points. You are looking at the interannual variation of the original data in HadCRUT4. This was shown in Figure 4A, not Figure 5A of Tung and Zhou (2013), PNAS. Figure 5A is the result of one round of MLR, after removal of ENSO, vol and solar influences. Figure 5B is the adjusted data, and it contains everything that remains after removal of ENSO, sol and solar, plus AMO influence. It should contain anthropogenic response plus climate noise ideally. In reality it also contains errors in observation and the interpolation that was used to come up with the global mean, especially in the early decades in the 20th century; the 50 years prior to that was especially bad, datawise. You can see that after 1970s, the variations about a linear trend do look smaller and like random noise.
KK Tung.
Your reply @190 describes itself as being a reply to me @188. I have to say that I am not entirely clear that it is.
I can see that it is a reply to me @170. But as I point out in my first paragraph @188, my comment @170 mistook Fig 2b in your 1st SkS post as being equivalent to Fig 5b of T&Zh13. And it is this Fig 2b that strangely still features the HadCRUT4 signal. Thus such a reply as yours @190 is commenting on a mistaken thesis - not a productive use of words.
My first paragraph @188 was solely by way of an apology for my mistaking that Fig 2b for Fig 5b (although the strangness of Fig 2b does remain unexplained and this may be an issue for yourself).
But enough of that initial paragraph @188.
You will surely note that @188 I present more than one paragraph. You will note that the second, third and fourth paragraph are the ones that lead up to my question which is the point at issue @188. Any response to my comment @188 would hopefully address these paragraphs and that question.
Now, it is not impossible that the final two sentences of your comment @190 could be construed as some sort of response to these final paragraphs. Yet they are so indirect and carry such implication that I find it hard to see them as a reply. If they are your reply, could you confirm as such. If they are not, a reply would be good.
In reply to MA Rodger at post 191:As I said, I didn't quite understand your question and so it would help if you could ask it again if my reply in post 190 was not satisfactory. In that reply I was trying to address your corrected version---note that it did not address the incorrect references to Figure 2. It contains two parts, the first part was that you should not take the wobbles in Figure5AB as the original interannual variation in HadCRUT4. It is Figure 4A that should serve that purpose. The second part was the last two sentences, which explain what the residual should contain in practice. Ideally, the residual (after the anthropogenic response) should contain only climate noise, but in practice, especially in early decades of the data record, it could contain data inadequacies. Some of these data problems could also be amplified by the MLR procedure: Some of the timing of the occurrences of El Nino warming events in the HadCRUT4 data may not be consistent with the ENSO index we used a century ago. So the MLR may produce a negative spike, while the warming spike still remains. We could allow a lag in response that optimizes the removal of ENSO variations in the early decades, but the same lag then messes up the recent decades, which have better data.
KK Tunk @192.
I think this dialogue would benefit from my restating of the question @188. If you feel that you have answered this question adequately @190 & @192 then do say (although I would be surprised if this were so).
I here introduce a graph below showing the data from Tung&Zhou2013 Figs 5A&B. It presents quite a few questions but I will kick off here by asking about the wobbles in the blue trace.
The blue trace is the 10-year rolling average of residuals from the MLR obtained by subtracting the QCO2(t) function (introduced in your first SkS post) from the data presented in Fig 5B, and obviously re-based for clarity's sake. According to Zhou &Tung 2013 which covers your MLR analysis more fully than T&Zh13 "The residual ... should only consist of climate noise if the MLR is successful..." This conforms to my understanding of it.
Yet the blue trace showing the residuals from the MLR analysis in Tung&Zhou2013 shows a lot more than "noise." There are distinct wobbles and these are not small wobbles being 43% that of the original HadCRUT4 wobbles (red trace). The residuals thus contain a very significant part of the HadCRUT4 signal which the MLR analysis has failed to attribute.
A cynic would point to such wobbles within the residuals as being indicative of curve-fitting.
For myself, I am more charitable and rather see the problem being that these wobbles have gone unreported in Tung&Zhou2013. Indeed, a very similar trace can also be derived from Fig 1B Zhou&Tung2013 yet that paper says of the data in Fig 1B "The global-mean temperature adjusted this way shows mostly a monotonic trend with some scatter." This blue trace is definitely not "scatter."
(Note that the graph below features data derived from your Fig 5A&B in Tung&Zhou2013 as there are other feature beyond the blue trace that I see requiring explanation & which I hope we can address in later comments.)
Could you thus explain why this wobble is present in the residuals and why its presence has remained unreported?
KK Tung.
With no reply from you to my questioning @193, I will assume that the comments @190 & @192 constitutes such a reply. While I take a little time to consider the full implications of those replies, I will present another aspect of the data graphed @193 which also requires some explanation. (And be advised that this is not the last of my enquiries about this data.)
The trace of the AMO signal shown in the graph @193 is obtained by subtracting the data presented in T&Zh13 Fig 5a from that in Fig 5b. This AMO signal raises two questions.
Firstly, this AMO signal used in your MLR is smoothed using LOWESS (as described in Zh&T13). This smoothing will smooth out inter-annual wobbles of ENSO or Sol or Vol that are present in the Enfield AMO data series. But such smoothing will not entirely remove ENSO, Sol & Vol. Indeed parts of these signals are still evident in your LOWESS smoothed AMO series. For instance, the inflection in the AMO signal 1980-90 is entirely the residual of two Volcanic wobbles (El Chi'chon & Pinatuba). Surely if AMO is to be used as a regressor then this LOWESS smoothing is allowing a smoothed and still significant ENSO, Sol & Vol signal to remain within that AMO signal. Can this be appropriate? Would it not be better to use, perhaps, MLR to remove ENSO, Sol & Vol from AMO prior to AMO's use in the HadCRUT4 MLR?
Secondly, there appears to be a problem with the more recent end of your smoothed AMO signal. I present the graph below by way of illustration. LOWESS smoothing of the AMO signal allows the signal to be smoothed to the very ends of the data.
The AMO signal has, of course, two ends. The 1856 end remains very flat despite the AMO index for 1856 averaging for more than a year 0.15 above your end-smoothed value. As a product of the smoothing process I have no problem with the flat 1856 end. Where things start to look awry is when this 1856 smoothing is compared with the smoothing at the 2000s end of the series.
The smoothed AMO signal from T&ZH13 Fig5 drops to its end 2007-2011 by 0.053. This is a considerable drop. In size it is over one sixth of the smoothed AMO's full value range. And it is crammed into a 4-year period. It is therefore a big drop.
This is all the more suprising as this drop is well over twice the drop of the smoothed AMO signal used in Zh&T13 Fig1 yet the inset in Zh&T13 clearly shows that Enfield AMO data to at least November 2011 has been used in Zh&T13. How then can T&Zh13 drop so much more than Zh&T13? In T&Zh13 the MLR does extend a further year to 2011 but, even if T&Zh13 included more recent data, any such extra data that is lower valued than your smoothed value (5 months worth) is far less significant than the 13 months-worth from 1856 that makes zero impact on the 1856 end. And, of course, the last year of Enfield AMO (some of which will post-date T&Zh13) is entirely above your smoothed value. As of now, there is no drop whatever!!
So can the large 2007-11 smoothed AMO drop used by T&Zh13 be explained?
In reply to MA Rodger at post 193:Ahh, I think I now understand your question. Figure 5B is the result of an MLR process, using a linear anthropogenic regressor. You wish to look at the residual of that MLR process, which was not shown in our PNAS paper. So you tried to reconstruct it by subtracting a posteri, an anthropogenic index QCO2, from a different set of MLR discussed in part 1 of my post, and found some significant wobbles. In that post I was trying to demonstrate the robustness of the adjusted data, which I said should ideally consist of anthropogenic response and climate noise, using very different anthropogenic regressors. It then follows that the residual---"climate noise"--- is compensating for the different anthropogenic regressor used. Therefore one cannot find out what the residual of one MLR is by subtracting out a different regressor. The QCO2 regressor was used only in part 1 off my post and a linear regressor was used in Figure 5 of our PNAS paper. I hope this answers your question.
Continued from post 195, the residual that you were looking for from the MLR analysis using QCO2 as the anthropogenic regressor was shown in Figure 3 in part 1 of my original post. No need to reconstruct.
KK Tung @ 195 & @196.
The question I posed @193 was "Could you thus explain why this wobble is present in the residuals and why its presence has remained unreported?"
You appear to agree @195 that the wobble is significant in that @195 you mention such phenomenon without disputing its existence within my graph @193.
But you say I am not graphing the residuals from T&Zh13 Fig 5 because that would require the subtraction of a linear function while I subtracted the QCO2(t) function. Yet I do not consider such detail relevant to my enquiry. If the subtraction is linear or QCO2(t), neither will make wobbles magically disappear.
@196 you suggest the inset at Fig 3 in your 1st SkS post usefully shows residuals. Let us examine these residuals as there can be no dispute that they are the actual residuals. In that 1st SkS post you describe these residuals in the inset as "Except for s a minor negative trend in the last decade in the Residual, it is almost just noise," but this is not correct.The residuals in Fig3 inset contains a wobble, a signal almost half the size of the original HadCRUT4 signal. This is illustrated in the attached graph where the residuals have been multipled by 2 to show how close they are to being half the size of the original HadCRUT4 signal.
A similar sized wobble is also present in the residuals of both the analyses graphed in Zh&T13 Fig 1 and T&Zh13 Fig 5. And the presence of such a wobble is important. After all, the final word of Zh&T13 was "Whether this method is successful can be judged by the reduced scatter in the adjusted data and by the residual’s resemblance to random noise."
So I repeat my question posed @193
Could you thus explain why this wobble is present in the residuals and why its presence has remained unreported?
KK Tung.
I did indicate @194 that I had further concerns stemming from the graph presened @193. With no prompt reply to the first two such concerns expressed @193/197 & @194 apparently forthcoming, perhaps presenting my remaining concerns would be helpful.
These last concerns from the graph @193 stem from the trace labelled SolVolENSO. This trace represents the total of the temperature changes attributed by the MLR to Solar, Volcanic & ENSO forcing and it is derived simply by subtracting the data within T&Zh13 fig5a from HadCRUT4. There are two features that I consider problematical within this SolVolENSO trace. Firstly its amplitude is so tiny. And secondly, along its entire series it is so flat.
Note that these two problems are also present in Zh&T13 fig 1a.
(1) In the graph @193, the spread of values in the SolVolENSO trace is visibly smaller than the spread of values in the HadCRUT4 trace labelled "Had oscillations" in that graph (which is HadCRUT4 - 10yearsAverageHadCRUT4). While there may be an explanation for this difference, Zh&T13 does say that it obtains results very close to the 1979-2010 results of Foster & Rahmsdorf 2011. (Zh&T13 does explain that its Fig 1a equivilant to T&Zh13 Fig5a is effectively the FR11 analysis but for 1856-2011). In FR11 the attributed temperatures & HadCRUT4 have very similar amplitude, and thus FR11 is able to attribute the majority of the fluctuations within the HadCRUT3 signal to Solar Volcanic & ENSO effects. It appears Zh&T13/T&Zh13 has failed to do likewise for HadCRUT4.
(2) The data used by T&Zh13 to create Fig 5a are as follows:- Sol = Wang et al 2005, Vol = Sato et al 1993 and ENSO = Cold Tongue Index. (As an aside, it would be interesting to learn how the lack of Cold Tongue data during the 1860s was overcome, given that the alternative MEI.ext was not chosen because it does not go back before 1871.) Given these three inputs, it would appear to me sensible to expect periods with long term trends within the SolVolENSO trace.
As an instance of this, consider the period 1910 to 1930. Solar forcing of course fluctuates with each solar cycle but there is a strong rising inter-cycle trend over solar cycles 14-19 which encompasses this entire 1910-30 period. Volcanic forcings also fluctuate with the individual volcanic eruptions yet these are diminishing over the period 1910-30 and would thus at the very least not counteract the rising Solar trend. CTI (and MEI.ext) also fluctuates but again too is rising significantly over the period 1910-30.
So why is it that when I plot SolVolENSO from T&Zh13 fig 5a, the 1910-30 plot does not feature any significant upward trend? Rather it is very flat, a flatness that extends over the rest of SolVolENSO with onlyshort sub-decadal trends being evident.
These two features of the MLR output SolVolENSO, coupled with the wobbles in the residuals (as discussed @193/197) and the problems with the AMO index used (as discussed @194) do, I feel, need some explanation. Otherwise the integrity of this MLR analysis becomes drawn into serious question.
I'm sorry for the long delay; my day job has consumed my life. I like your new simulation, and tried to reproduce it in R, though I used a Fourier transform band pass filter instead of wavelets. Regardless, the human and natural influences look similar to those in Dr. Tung's plots (which are sadly no longer visible in his comment).
My first tests had 10,000 Monte Carlo simulations each:
They varied so much that I ran a few tests with 10,000,000 simulations each:
I also tried matching ARMA(p,q) noise parameters to those of the real residuals.
I still don't know why the mean trends vary so much when using 10,000 Monte Carlo simulations. I agree with Dr. Tung that millions of runs shouldn't be necessary, but for some reason "merely" 10,000 runs yield wildly varying results. More disturbingly, none of the trends in either of the 10,000,000 runs overlap with the mean trend in some of the 10,000 run cases. Maybe I'm not using the random number generator correctly?
Without seeing how Dr. Tung's code differs from mine, I don't know how he was able to specify the percentage of 10,000 simulations that contained the true trend to two significant digits ("91%") when my estimates vary from 2% to 100%, and most of those 20,070,000 white noise simulations don't include the true trend.
That's a fair point; I should've qualified those statements as my opinion to avoid implying that everyone agrees. Personally, I read Huber and Knutti's statement as a criticism of the optimal fingerprint method because it doesn't consider or conserve the energy budget. This is an unusual situation where I've criticized fingerprints used by the IPCC and many researchers while agreeing with Dr. Pielke Sr. that ocean heat content is a better diagnostic than surface temperatures or stratospheric cooling fingerprints, etc. In my opinion, diagnostics more closely related to conservation of energy are more compelling. But you're right, this is just my opinion.
Why isn't this part based on a thermodynamic argument? Since CMIP3 models have internal ocean variability, aren't they're simulating heat transfer between the deep ocean and surface (i.e. thermodynamics)?
Attribution over the last 50 years is based on Fig. 3(c) from Huber and Knutti 2012:
Given mean radiative forcings (etc.), the upper bound on the post-1950 surface trend due to internal variability is 26%. The lower bound is -26%, implying that internal variability actually offset surface warming. Regarding the "+/-12%" Huber and Knutti state "The probabilistic ranges presented here account for uncertainties in the observations, radiative forcing, internal variability and model inadequacy (see Methods)."
Since the upper bound in Huber and Knutti is itself given as a probabilistic range, I don't see why Dr. Tung's singular estimate of "40%" should be compared to the upper bound of the upper bound rather than the best estimate of the upper bound.
Even if we compare your estimate to the upper bound on the upper bound of Huber and Knutti 2012, the probabilistic range on that upper bound at least attempts to account for "model inadequacy." And 38% here is the upper bound on the upper bound of all modes of natural variability summed together. Even if this upper bound on the upper bound is appropriate and needs to be expanded because it didn't fully account for model inadequacy... doesn't this leave very little room for the PDO (for instance) to affect surface temperatures (at the same phase)?
Yes, all thermodynamic estimates involve simplifications but in my opinion simplifications are preferable to not mentioning energy or heat altogether. And 40% here is the upper bound of all modes of natural variability summed together. Even if this upper bound needs to be expanded... doesn't this leave very little room for the PDO (for instance) to affect surface temperatures (at the same phase)?