Arguments
The greenhouse effect and the 2nd law of thermodynamics
What the science says...
| Select a level... |
Basic
|
Intermediate
| |||
|
The 2nd law of thermodynamics is consistent with the greenhouse effect which is directly observed. |
|||||
2nd law of thermodynamics contradicts greenhouse theory
"The atmospheric greenhouse effect, an idea that many authors trace back to the traditional works of Fourier 1824, Tyndall 1861, and Arrhenius 1896, and which is still supported in global climatology, essentially describes a fictitious mechanism, in which a planetary atmosphere acts as a heat pump driven by an environment that is radiatively interacting with but radiatively equilibrated to the atmospheric system. According to the second law of thermodynamics such a planetary machine can never exist." (Gerhard Gerlich)
At a glance
Although this topic may have a highly technical feel to it, thermodynamics is a big part of all our everyday lives. So while you are reading, do remember that there are glossary entries available for all thinly underlined terms - just hover your mouse cursor over them for the entry to appear.
Thermodynamics is the branch of physics that describes how energy interacts within systems. That interaction determines, for example, how we stay cosy or freeze to death. You wear less clothing in very hot weather and layer-up or add extra blankets to your bed when it's cold because such things control how energy interacts with your own body and therefore your degree of comfort and, in extreme cases, safety.
The human body and its surroundings and energy transfer between them make up one such system with which we are all familiar. But let's go a lot bigger here and think about heat energy and its transfer between the Sun, Earth's land/ocean surfaces, the atmosphere and the cosmos.
Sunshine hits the top of our atmosphere and some of it makes it down to the surface, where it heats up the ground and the oceans alike. These in turn give off heat in the form of invisible but warming infra-red radiation. But you can see the effects of that radiation - think of the heat-shimmer you see over a tarmac road-surface on a hot sunny day.
A proportion of that radiation goes back up through the atmosphere and escapes to space. But another proportion of it is absorbed by greenhouse gas molecules, such as water vapour, carbon dioxide and methane. Heating up themselves, those molecules then re-emit that heat energy in all directions including downwards. Due to the greenhouse effect, the total loss of that outgoing radiation is avoided and the cooling of Earth's surface is thereby inhibited. Without that extra blanket, Earth's average temperature would be more than thirty degrees Celsius cooler than is currently the case.
That's all in accordance with the laws of Thermodynamics. The First Law of Thermodynamics states that the total energy of an isolated system is constant - while energy can be transformed from one form to another it can be neither created nor destroyed. The Second Law does not state that the only flow of energy is from hot to cold - but instead that the net sum of the energy flows will be from hot to cold. That qualifier term, 'net', is the important one here. The Earth alone is not a "closed system", but is part of a constant, net energy flow from the Sun, to Earth and back out to space. Greenhouse gases simply inhibit part of that net flow, by returning some of the outgoing energy back towards Earth's surface.
The myth that the greenhouse effect is contrary to the second law of thermodynamics is mostly based on a very long 2009 paper by two German scientists (not climate scientists), Gerlich and Tscheuschner (G&T). In its title, the paper claimed to take down the theory that heat being trapped by our atmosphere keeps us warm. That's a huge claim to make – akin to stating there is no gravity.
The G&T paper has been the subject of many detailed rebuttals over the years since its publication. That's because one thing that makes the scientific community sit up and take notice is when something making big claims is published but which is so blatantly incorrect. To fully deal with every mistake contained in the paper, this rebuttal would have to be thousands of words long. A shorter riposte, posted in a discussion on the topic at the Quora website, was as follows: “...I might add that if G&T were correct they used dozens of rambling pages to prove that blankets can’t keep you warm at night."
If the Second Law of Thermodynamics is true - something we can safely assume – then, “blankets can’t keep you warm at night”, must be false. And - as you'll know from your own experiences - that is of course the case!
Please use this form to provide feedback about this new "At a glance" section. Read a more technical version below or dig deeper via the tabs above!
Further details
Among the junk-science themes promoted by climate science deniers is the claim that the explanation for global warming contradicts the second law of thermodynamics. Does it? Of course not (Halpern et al. 2010), but let's explore. Firstly, we need to know how thermal energy transfer works with particular regard to Earth's atmosphere. Then, we need to know what the second law of thermodynamics is, and how it applies to global warming.
Thermal energy is transferred through systems in five main ways: conduction, convection, advection, latent heat and, last but not least, radiation. We'll take them one by one.
Conduction is important in some solids – think of how a cold metal spoon placed in a pot of boiling water can become too hot to touch. In many fluids and gases, conduction is much less important. There are a few exceptions, such as mercury, a metal whose melting point is so low it exists as a liquid above -38 degrees Celsius, making it a handy temperature-marker in thermometers. But air's thermal conductivity is so low we can more or less count it out from this discussion.
Convection
Figure 1: Severe thunderstorm developing over the Welsh countryside one evening in August 2020. This excellent example of convection had strong enough updraughts to produce hail up to 2.5 cm in diameter. (Source: John Mason)
Hot air rises – that's why hot air balloons work, because warm air is less dense than its colder surroundings, making the artificially heated air in the balloon more buoyant and thereby creating a convective current. The same principle applies in nature: convection is the upward transfer of heat in a fluid or a gas.
Convection is highly important in Earth's atmosphere and especially in its lower part, where most of our weather goes on. On a nice day, convection may be noticed as birds soar and spiral upwards on thermals, gaining height with the help of that rising warm air-current. On other days, mass-ascent of warm, moist air can result in any type of convective weather from showers to severe thunderstorms with their attendant hazards. In the most extreme examples like supercells, that convective ascent or updraught can reach speeds getting on for a hundred miles per hour. Such powerful convective currents can keep hailstones held high in the storm-cloud for long enough to grow to golfball size or larger.
Advection
Advection is the quasi-horizontal transport of a fluid or gas with its attendant properties. Here are a couple of examples. In the Northern Hemisphere, southerly winds bring mild to warm air from the tropics northwards. During the rapid transition from a cold spell to a warm southerly over Europe in early December 2022, the temperatures over parts of the UK leapt from around -10C to +14C in one weekend, due to warm air advection. Advection can also lead to certain specific phenomena such as sea-fogs – when warm air inland is transported over the surrounding cold seas, causing rapid condensation of water vapour near the air-sea interface.
Figure 2: Advection fog completely obscures Cardigan Bay, off the west coast of Wales, on an April afternoon in 2015, Air warmed over the land was advected seawards, where its moisture promptly condensed over the much colder sea surface.
Latent heat
Latent heat is the thermal energy released or absorbed during a substance's transition from solid to liquid, liquid to vapour or vice-versa. To fuse, or melt, a solid or to boil a liquid, it is necessary to add thermal energy to a system, whereas when a vapour condenses or a liquid freezes, energy is released. The amount of energy involved varies from one substance to another: to melt iron you need a furnace but with an ice cube you only need to leave it at room-temperature for a while. Such variations from one substance to another are expressed as specific latent heats of fusion or vapourisation, measured in amount of energy (KiloJoules) per kilogram. In the case of Earth's atmosphere, the only substance of major importance with regard to latent heat is water, because at the range of temperatures present, it's the only component that is both abundant and constantly transitioning between solid, liquid and vapour phases.
Radiation
Radiation is the transfer of energy as electromagnetic rays, emitted by any heated surface. Electromagnetic radiation runs from long-wave - radio waves, microwaves, infra-red (IR), through the visible-light spectrum, down to short-wave – ultra-violet (UV), x-rays and gamma-rays. Although you cannot see IR radiation, you can feel it warming you when you sit by a fire. Indeed, the visible part of the spectrum used to be called “luminous heat” and the invisible IR radiation “non-luminous heat”, back in the 1800s when such things were slowly being figured-out.
Sunshine is an example of radiation. Unlike conduction and convection, radiation has the distinction of being able to travel from its source straight through the vacuum of space. Thus, Solar radiation travels through that vacuum for some 150 million kilometres, to reach our planet at a near-constant rate. Some Solar radiation, especially short-wave UV light, is absorbed by our atmosphere. Some is reflected straight back to space by cloud-tops. The rest makes it all the way down to the ground, where it is reflected from lighter surfaces or absorbed by darker ones. That's why black tarmac road surfaces can heat up until they melt on a bright summer's day.
Figure 3: Heat haze above a warmed road-surface, Lincoln Way in San Francisco, California. May 2007. Image: Wikimedia Commons.
Energy balance
What has all of the above got to do with global warming? Well, through its radiation-flux, the Sun heats the atmosphere, the surfaces of land and oceans. The surfaces heated by solar radiation in turn emit infrared radiation, some of which can escape directly into space, but some of which is absorbed by the greenhouse gases in the atmosphere, mostly carbon dioxide, water vapour, and methane. Greenhouse gases not only slow down the loss of energy from the surface, but also re-radiate that energy, some of which is directed back down towards the surface, increasing the surface temperature and increasing how much energy is radiated from the surface. Overall, this process leads to a state where the surface is warmer than it would be in the absence of an atmosphere with greenhouse gases. On average, the amount of energy radiated back into space matches the amount of energy being received from the Sun, but there's a slight imbalance that we'll come to.
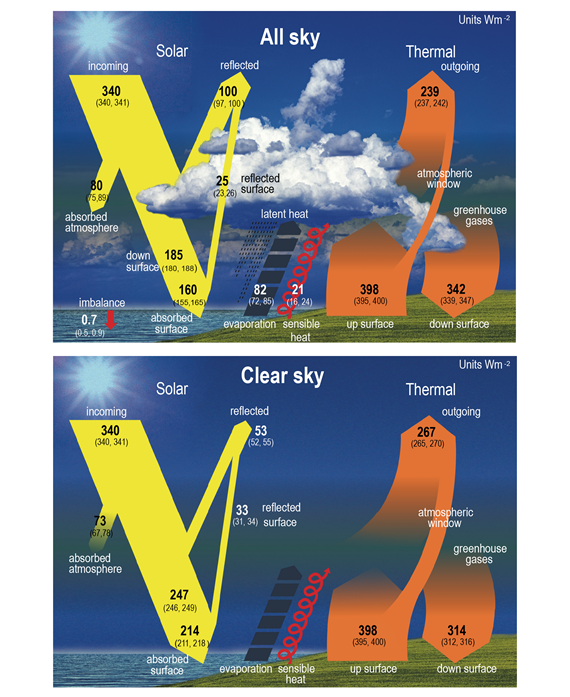
If this system was severely out of balance either way, the planet would have either frozen or overheated millions of years ago. Instead the planet's climate is (or at least was) stable, broadly speaking. Its temperatures generally stay within bounds that allow life to thrive. It's all about energy balance. Figure 4 shows the numbers.
Figure 4: Schematic representation of the global mean energy budget of the Earth (upper panel), and its equivalent without considerations of cloud effects (lower panel). Numbers indicate best estimates for the magnitudes of the globally averaged energy balance components in W m–2 together with their uncertainty ranges in parentheses (5–95% confidence range), representing climate conditions at the beginning of the 21st century. Figure adapted for IPCC AR6 WG1 Chapter 7, from Wild et al. (2015).
While the flow in and out of our atmosphere from or to space is essentially the same, the atmosphere is inhibiting the cooling of the Earth, storing that energy mostly near its surface. If it were simply a case of sunshine straight in, infra-red straight back out, which would occur if the atmosphere was transparent to infra-red (it isn't) – or indeed if there was no atmosphere, Earth would have a similar temperature-range to the essentially airless Moon. On the Lunar equator, daytime heating can raise the temperature to a searing 120OC, but unimpeded radiative cooling means that at night, it gets down to around -130OC. No atmosphere as such, no greenhouse effect.
Clearly, the concentrations of greenhouse gases determine their energy storage capacity and therefore the greenhouse effect's strength. This is particularly the case for those gases that are non-condensing at atmospheric temperatures. Of those non-condensing gases, carbon dioxide is the most important. Because it only exists as vapour, the main way it is removed is as a weak solution of carbonic acid in rainwater – indeed the old name for carbon dioxide was 'carbonic acid gas'. That means once it's up there, it has a long 'atmospheric residency', meaning it takes a long time to be removed.
Earth’s temperature can be stable over long periods of time, but to make that possible, incoming energy and outgoing energy have to be exactly the same, in a state of balance known as ‘radiative equilibrium’. That equilibrium can be disturbed by changing the forcing caused by any components of the system. Thus, for example, as the concentration of carbon dioxide has fluctuated over geological time, mostly on gradual time-scales but in some cases abruptly, so has the planet's energy storage capacity. Such fluctuations have in turn determined Earth's climate state, Hothouse or Icehouse – the latter defined as having Polar ice-caps present, of whatever size. Currently, Earth’s energy budget imbalance averages out at just under +1 watt per square metre - that’s global warming.
That's all in accordance with the laws of Thermodynamics. The First Law of Thermodynamics states that the total energy of an isolated system is constant - while energy can be transformed from one component to another it can be neither created nor destroyed. Self-evidently, the "isolated" part of the law must require that the sun and the cosmos be included. They are both components of the system: without the Sun as the prime energy generator, Earth would be frozen and lifeless; with the Sun but without Earth's emitted energy dispersing out into space, the planet would cook, Just thinking about Earth's surface and atmosphere in isolation is to ignore two of this system's most important components.
The Second Law of Thermodynamics does not state that the only flow of energy is from hot to cold - but instead that the net sum of the energy flows will be from hot to cold. To reiterate, the qualifier term, 'net', is the important one here. In the case of the Earth-Sun system, it is again necessary to consider all of the components and their interactions: the sunshine, the warmed surface giving off IR radiation into the cooler atmosphere, the greenhouse gases re-emitting that radiation in all directions and finally the radiation emitted from the top of our atmosphere, to disperse out into the cold depths of space. That energy is not destroyed – it just disperses in all directions into the cold vastness out there. Some of it even heads towards the Sun too - since infra-red radiation has no way of determining that it is heading towards a much hotter body than the Earth,
Earth’s energy budget makes sure that all portions of the system are accounted for and this is routinely done in climate models. No violations exist. Greenhouse gases return some of the energy back towards Earth's surface but the net flow is still out into space. John Tyndall, in a lecture to the Royal Institution in 1859, recognised this. He said:
As long as carbon emissions continue to rise, so will that planetary energy imbalance. Therefore, the only way to take the situation back towards stability is to reduce those emissions.
Update June 2023:
For additional links to relevant blog posts, please look at the "Further Reading" box, below.
Last updated on 29 June 2023 by John Mason. View Archives
In this model we have light entering a box (A) at an angle. It then strikes a mirror on the back of the box, is reflected of a mirror on the front of the box so placed that it does not block any incoming light. The now twice reflected light returns to the back of the box, striking the mirror once more. It then goes through a second transparent zone in the front of the box.
Assume the ideal case in which all apertures are 100% transparent, all mirrors are 100% reflective and flat, and in which the light is so angled that neither the incoming beam (A) nor the outgoing beam (C) strike any part of the mirror on the top of the box. In that case, after sufficient time for light to transit the box three times, and with a constant light source providing beam (A), then the box will have the following equalities:
1) Incoming light (A) = Outgoing light (C) (by virtue of conservation of energy).
2) Light reflected from the lid (D) = Outgoing light (C).
3) Light reflected from the back = light striking the underside of the lid (B) = light transmitted by the lid (C) plus light reflected by the lid (D) (by virtue of conservation of energy). This may require a little clarification. The lid consists of three sections in this model, two transparent, and one mirrored on the underside. One transparent section allows in the incoming light (A). The other allows out the outgoing light (C). So the light striking the back of the lid equals the light striking the mirrored section plus the light striking the transparent section through which the light exits.
Therefore
4) Light reflected from the back of the box (B) = light reflected from the back of the lid (D) plus Incoming light (A) = 2 x A (again, by conservation of energy.
Such a box clearly does not violate any law of thermodynamics. If it did violate such laws, so much the worse for those laws, for the box could be set up as a primary school science project, and will behave as advertised. As I assume that the scientists of the world are not part of a massive conspiracy to foist upon us "laws" that can be refuted by any primary school kid with a plate of glass and two mirrors, I will take it that this box does not violate the laws fo thermodynamics is beyond dispute.
However, having said that, we should notice that in each time interval equal to the time it takes a photon to travel from the lid to the back wall:
5) the accumulated photons at equilibrium is 4 times the number of photons that enter the light box at each time interval; and
6) at equilibrium the number of photons reflected in each time interval is 3 times the number that enter the light box in each time interval. Of those, 2 times that number are reflected of the back wall, and a number of photons equal to the number that enter are reflected of the lid. This ignores reflections of the side walls which are irrelevant to the overall issue.
Now, reconsider this model:
The description of the model is found in comment 615 above. Essentially, however, it is the same model as above, except the lid is replaced by a lid which lets in all light from outside and reflects exactly half of light from the inside, transmitting the remainder. The walls are perfectly mirrored.
After equilibrium is established (ie, in approximately 20 times the time it takes for light to travel from the lid to the back of the box, see Phil's comment @624 and my comments @626 and @640 above), the equalities (1) to (4) above hold of this box as well (with appropriate adjustment of wording - for exact wording see comment 615 above).
However, the facts (5) and (6) also hold of this box (see comment 647 above). Now, these two facts, according to some people, create a problem for this model. According to those people, they cause it to violate the laws of thermodynamics. But as we have seen, our first model (in this comment) has exactly these two properties, and does not violate the laws of thermodynamics. Therefore this model does not violate the laws of thermodynamics either. In fact, the only interesting difference between this model and the previous one is that this model takes about five times as long to reach equilibrium.
So, having established beyond reasonable doubt that the simple light box does not violate the laws of thermodynamics, consider the following model:
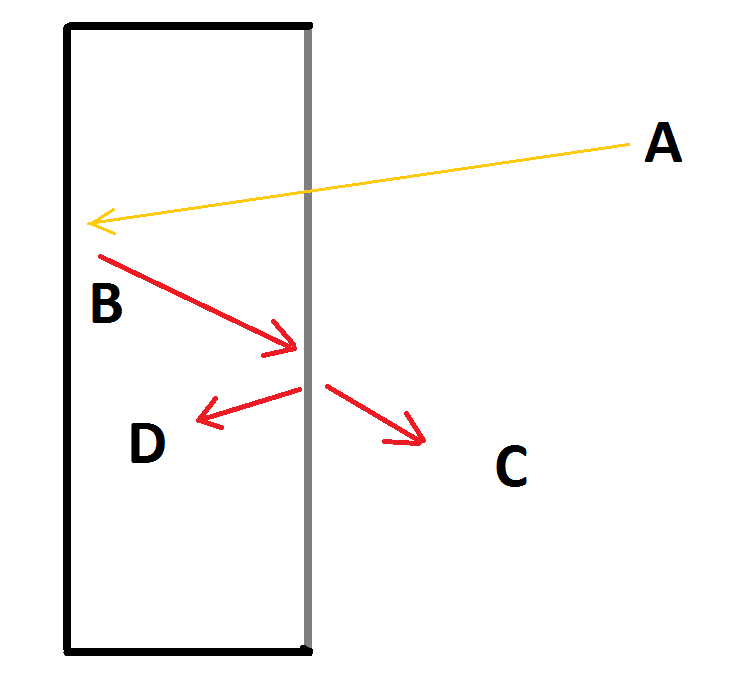This model is quite different from the preceding two. For a start, (in the ideal case) the back and walls are perfectly absorbing on the inside, and perfectly reflective at all wavelengths on the outside. This means any light entering the box will be absorbed by the box, warming the back of the box. We also suspend the box in a vacuum so that energy can only escape by radiation. Because the outside of the walls and back are perfectly reflective, this means they have zero emissivity and energy can only escape through the lid.
The lid itself has (in the ideal case)perfect thermal isolation from the sides, and back (which means the box contains a vacuum). It is perfectly transparent to all light below a certain wavelength, and perfectly absorbing for all wavelengths above that amount. It (and the back and walls of the box) is also a perfect thermal conductor so that its outside and inside have exactly the same temperature.
Importantly, the wavelength of the incoming light is less than the critical wavelength of the lid. Also, for simplicity, the total energy of the incoming light is less than the amount at which the shortest wavelength of a black body emission from the back and sides of the box is shorter than the critical wavelength.
Given these conditions, when you start shining light on the box, the back and sides will heat up and start emitting long wave length radiation. Because all of that radiation has a wavelength longer than the critical value of the lid, the lid will in turn start heating up and emit radiation. Eventually the energy emitted outwards (C) will equal the energy of the incoming light (A), at which time equilibrium has been reached.
At that time, the following equalities will hold:
1) Incoming energy (A) = Outgoing energy (C) (by virtue of conservation of energy).
2) energy radiated from the lid inwards(D) = Outgoing energy (C) (by virtue of both sides of the lid having the same temperature and emissivity).
3) energy radiated from the back = energy absorbed by the underside of the lid (B) = energy radiated outwards by the lid (C) plus energy radiate inwards by the lid (D) (by virtue of conservation of energy).
Therefore
4) Energy radiated from the back of the box (B) = energy radiated inwards by the lid (D) plus Incoming energy (A) = 2 x A (again, by conservation of energy).
It will also be true that:
5) The accumulated energy in the box in the form of radiation will be four times the energy carried into the box by incoming light in the time it takes for light to travel from the lid to the back of the box.
Indeed, an additional amount of energy will be stored in the back, sides and lids of the box depending on their heat capacity. That means the greater their heat capacity, the longer the box will take to reach equilibrium. That is simple a consequence of the incoming energy being diverted to heat the wall and lid, and therefore not being available to leave the box. It is only when the walls and lid reach a stable temperature that the energy is no longer used in the box, and will leave at the same rate it entered.
Now, very clearly, these 5 facts mirror the first 5 facts in our first, and second model. Therefore, if those five facts do not cause the first two models to violate the laws of thermodynamics (which they do not), then these facts cannot cause the third model to violate the laws of thermodynamics. In fact, the only thermodynamically interesting difference between the first two and the third model is that in the first two, the leaving energy had an almost identical entropy to the incoming energy, whereas in this model, the leaving energy has a much higher entropy in virtue of its much longer wavelengths.
The other interesting fact about this model is that it is an example of (not an analogy to, but an example of) the green house effect. It is a very simple example, but example it is none-the-less. And as this example does not violate any law of thermodynamics, it follows that the greenhouse effect does not violate any law of thermodynamics.
QED
Climate Myth...