Is the CO2 effect saturated?
What the science says...
| Select a level... |
 Basic
Basic
|
 Intermediate
Intermediate
|
 Advanced
Advanced
| ||||
|
The notion that the CO2 effect is 'saturated' is based on a misunderstanding of how the greenhouse effect works. |
|||||||
Climate Myth...
CO2 effect is saturated
"Each unit of CO2 you put into the atmosphere has less and less of a warming impact. Once the atmosphere reaches a saturation point, additional input of CO2 will not really have any major impact. It's like putting insulation in your attic. They give a recommended amount and after that you can stack the insulation up to the roof and it's going to have no impact." (Marc Morano, as quoted by Steve Eliot)
At-a-Glance
This myth relies on the use (or in fact misuse) of a particular word – 'saturated'. When someone comes in from a prolonged downpour, they may well exclaim that they are saturated. They cannot imagine being any wetter. That's casual usage, though.
In science, 'saturated' is a strictly-defined term. For example, in a saturated salt solution, no more salt will dissolve, period. But what's that got to do with heat transfer in Earth's atmosphere? Let's take a look.
Heat-trapping by CO2 in the atmosphere happens because it has the ability to absorb and pass on infra-red radiation – it is a 'greenhouse gas'. Infra-red is just one part of the electromagnetic spectrum, divided by physicists into a series of bands. From the low-frequency end of the spectrum upwards, the bands are as follows: radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays. Gamma rays thus have a very high-frequency. They are the highest-energy form of radiation.
As our understanding of the electromagnetic spectrum developed, it was realised that the radiation consists of particles called 'photons', travelling in waves. The term was coined in 1926 by the celebrated physicist Gilbert Lewis (1875-1946). A photon's energy is related to its wavelength. The shorter the wavelength, the higher the energy, so that the very high-energy gamma-rays have the shortest wavelength of the lot.
Sunshine consists mostly of ultraviolet, visible light and infra-red photons. Objects warmed by the sun then re-emit energy photons at infra-red wavelengths. Like other greenhouse gases, CO2 has the ability to absorb infra-red photons. But CO2 is unlike a mop, which has to be wrung out regularly in order for it to continue working. CO2 molecules do not get filled up with infra-red photons. Not only do they emit their own infra-red photons, but also they are constantly colliding with neighbouring molecules in the air. The constant collisions are important. Every time they happen, energy is shared out between the colliding molecules.
Through those emissions and collisions, CO2 molecules constantly warm their surroundings. This goes on all the time and at all levels in the atmosphere. You cannot say, “CO2 is saturated because the surface-emitted IR is rapidly absorbed”, because you need to take into account the whole atmosphere and its constant, ongoing energy-exchange processes. That means taking into account all absorption, all re-emission, all collisions, all heating and cooling and all eventual loss to space, at all levels.
If the amount of radiation lost to space is equal to the amount coming in from the Sun, Earth is said to be in energy balance. But if the strength of the greenhouse effect is increased, the amount of energy escaping falls behind the amount that is incoming. Earth is then said to be in an energy imbalance and the climate heats up. Double the CO2 concentration and you get a few degrees of warming: double it again and you get a few more and on and on it goes. There is no room for complacency here. By the time just one doubling has occurred, the planet would already be unrecognisable. The insulation analogy in the myth is misleading because it over-simplifies what happens in the atmosphere.
Please use this form to provide feedback about this new "At a glance" section. Read a more technical version below or dig deeper via the tabs above!
Further details
This myth relies on the use of a word – saturated. When we think of saturated in everyday use, the term 'soggy' comes to mind. This is a good example of a word that has one meaning in common parlance but another very specific one when thinking about atmospheric physics. Other such words come to mind too. Absorb and emit are two good examples relevant to this topic and we’ll discuss how they relate to atmospheric processes below.
First things first. The effect of CO2 in the atmosphere is due to its influence on the transport of 'electromagnetic radiation' (EMR). EMR is energy that is moving as x-rays, ultraviolet (UV) light, visible light, infrared (IR) radiation and so on (fig. 1). Radiation is unusual in the sense that it contains energy but it is also always moving, at the speed of light, so it is also a form of transport. Radiation is also unusual in that it has properties of particles but also travels with the properties of waves, so we talk about its wavelength.
The particles making up radiation are known as photons. Each photon contains a specific amount of energy, and that is related to its wavelength. High energy photons have short wavelengths, and low energy photons have longer wavelengths. In climate, we are interested in two main radiation categories - firstly the visible light plus UV and minor IR that together make up sunshine, and secondly the IR from the earth-atmosphere system.
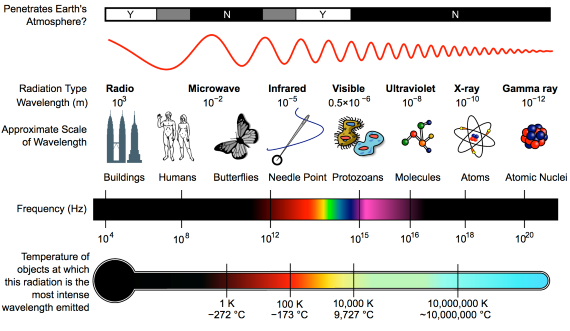
Fig. 1: diagram showing the full electromagnetic spectrum and its properties of the different bands. Image: CC BY-SA 3.0 from Wikimedia.
CO2 has the ability to absorb IR photons – it is a 'greenhouse gas'.So what does “absorb” mean, when talking about radiation? We are all familiar with using a sponge to mop up a water spill. The sponge will only absorb so much and will not absorb any more unless it's wrung out. In everyday language it may be described, without measurements, as 'saturated'. In this household example, 'absorb' basically means 'soak up' and 'saturated' simply means 'full to capacity'. Scientific terms are, in contrast, strictly defined.
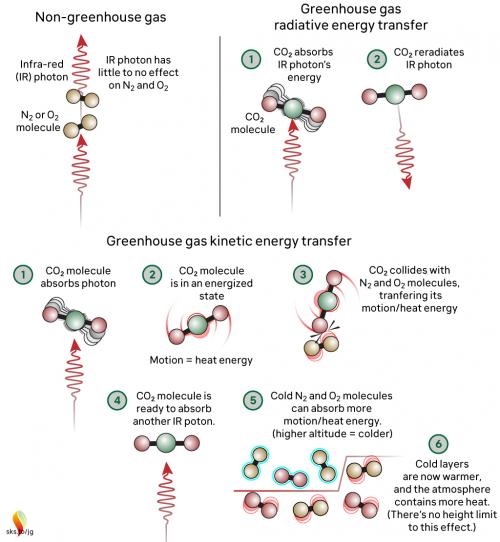
Now let's look at the atmosphere. The greenhouse effect works like this: energy arrives from the sun in the form of visible light and ultraviolet radiation. A proportion reaches and warms Earth's surface. Earth then emits the energy in the form of photons of IR radiation.
Greenhouse gases in the atmosphere, such as CO2 molecules, absorb some of this IR radiation, then re-emit it in all directions - including back to Earth's surface. The CO2 molecule does not fill up with IR photons, running out of space for any more. Instead, the CO2 molecule absorbs the energy from the IR photon and the photon ceases to be. The CO2 molecule now contains more energy, but that is transient since the molecule emits its own IR photons. Not only that: it's constantly colliding with other molecules such as N2 and O2 in the surrounding air. In those collisions, that excess energy is shared with them. This energy-sharing causes the nearby air to heat up (fig. 2).
Fig. 2: The greenhouse effect in action, showing the interactions between molecules. The interactions happen at all levels of the atmosphere and are constantly ongoing. Graphic: jg.
The capacity for CO2 to absorb photons is almost limitless. The CO2 molecule can also receive energy from collisions with other molecules, and it can lose energy by emitting IR radiation. When a photon is emitted, we’re not bringing a photon out of storage - we are bringing energy out of storage and turning it into a photon, travelling away at the speed of light. So CO2 is constantly absorbing IR radiation, constantly emitting IR radiation and constantly sharing energy with the surrounding air molecules. To understand the role of CO2, we need to consider all these forms of energy storage and transport.
So, where does 'saturation' get used in climate change contrarianism? The most common way they try to frame things is to claim that IR emitted from the surface, in the wavelengths where CO2 absorbs, is all absorbed fairly close to the surface. Therefore, the story continues, adding more CO2 can’t make any more difference. This is inaccurate through omission, because either innocently or deliberately, it ignores the rest of the picture, where energy is constantly being exchanged with other molecules by collisions and CO2 is constantly emitting IR radiation. This means that there is always IR radiation being emitted upwards by CO2 at all levels in the atmosphere. It might not have originated from the surface, but IR radiation is still present in the wavelengths that CO2 absorbs and emits. When emitted in the upper atmosphere, it can and will be lost to space.
When you include all the energy transfers related to the CO2 absorption of IR radiation – the transfer to other molecules, the emission, and both the upward and downward energy fluxes at all altitudes - then we find that adding CO2 to our current atmosphere acts to inhibit the transfer of radiative energy throughout that atmosphere and, ultimately, into space. This will lead to additional warming until the amount of energy being lost to space matches what is being received. This is precisely what is happening.
The myth reproduced at the top – incorrectly stating an analogy with roof insulation in that each unit has less of an effect - is misleading. Doubling CO2 from 280 ppm to 560 ppm will cause a few degrees of warming. Doubling again (560 to 1130 ppm) will cause a similar amount of additional warming, and so on. Many doublings later there may be a point where adding more CO2 has little effect, but recent work has cast serious doubt on that (He et al. 2023). But we are a long, long way from reaching that point and in any case we do not want to go anywhere near it! One doubling will be serious enough.
Finally, directly observing the specific, global radiative forcing caused by well-mixed greenhouse gases has - to date - proven elusive. This is because of irregular, uncalibrated or limited areal measurements. But very recently, results have been published regarding the deep reinterrogation of years of data (2003-2021) from the Atmospheric Infrared Sounder (AIRS) instrument on NASA's Aqua Satellite (Raghuraman et al. 2023). The work may well have finally cracked the long-standing issue of how to make finely detailed, consistent wavelength-specific measurements of outgoing long-wave radiation from Earth into space. As such, it has opened the way to direct monitoring of the radiative impact (i.e. forcing + feedback) of greenhouse gas concentration changes, thereby complimenting the Keeling Curve - the longstanding dataset of measured CO2 concentrations, down at the planet's surface.
Note: Several people in addition to John Mason were involved with updating this basic level rebuttal, namely Bob Loblaw, Ken Rice and John Garrett (jg).
Last updated on 31 December 2023 by John Mason. View Archives































 Arguments
Arguments





































OldHickory @ 646 and 648
Although you have not explicitly stated your definition of "saturation", the reference you provide to Barton Paul Levenson's web page suggests that you are making the argument based on transmission through a finite distance of a medium, as calculated from the Beer-Lambert law.
The Beer-Lambert Law is an exponential decay, and as a result the absorption never reaches 100%. Thus, to use it as an argument for "saturation", you need to make an argument of the form "this is close enough to 100% for all practical purposes". On Levenson's page, he uses 99% to perform the calculations he presents in his table 1.
The catch is, for any given distance you choose where absorption is 99% (and transmission is 1%), I can give you a shorter distance where absorption is less than 99% - even as low as 1%, if I make it short enough. Even if you choose something more that 99%, I can always choose a shorter path with a much lower absorption total.
Let's call your distance L1, and my distance L2. Your "saturation" argument is that increasing CO2 will have a negligible change on tramission through the layer to L1, since it is already almost 100%. But it will have an effect. If the original result is 99%, and increasing the absorption so that it is now 99.6%, is the change important? Well, you will probably argue that 99% and 99.6% are "the same for all practical purposes" - in fact, your "saturation" argument is completely dependent on making such a claim.
But what is the difference if we look at my distance. L2? What was 1% absorption is now 1.2%, and your saturation argument also depends on claiming that 1% and 1.2% are "the same for all practical purposes". The catch is, they are not. We are nowhere close to "saturation", and absorbing 1.2X greater radiation is significant.
One of the major factors in the radiative transfer equations is that absorbed radiation energy will most likely eventually be emitted again, and that emission will be equally likely to be up or down. Small changes in absorption lead to a larger number of absorbed/reemitted cycles before radiation is lost to space from the upper atmosphere, and as that number increases, so does the radiative greenhouse effect.
Your "saturation" argument depends on looking at the process as a single layer, thick enough that you reach "close enough to 100% for all practical purposes", and it fails because you are rolling the effect of many atmospheric layers into one.
I suggest that you read this post on the Beer-Lambert Law (including the comments).
OldHickory:
Further to your comment 646, you say
This is also incorrect, for more than one reason. When the lower atmosphere warms, if will hold more water vapour. More water vapour will affect radiation transfer, because your "saturation" argument is wrong. And since the lower and upper atmosphere are linked together into a complex energy balance, what happens in the lower atmosphere does not stay in the lower atmosphere. We do not require that the warming happen in the upper atmosphere - in fact I have already given you a reference to a paper and a figure (in comment 645) that shows that the upper troposphere does not warm in response to increased CO2.
Manabe and Wetherald, 1967
That paper gives extensive discussion of the role that water vapour plays. In fact, the title of that paper "Thermal Equilibrium of the Atmosphere with a Given Distribution of Relative Humidity" is a direct indication of the purpose of that study. It contrasts with an earlier paper that assumed constant absolute humidity - i.e., no water vapour feedback. The earlier paper is:
Manabe and Strickler, 1964
Read those two papers. Look at the figures, sort out why the two models are different and why their results are different.
[BL] OldHickory has been identified as a sock puppet of a previously banned user, so no further comments will be appearing from him.
CloudySky @653 (and recent others) :
You yourself will be "heavily funded" [your quote] by the Nobel Committee for Physics, just as soon as you publish your scientific paper showing that the surface temperature of Venus [about 460 degreesC] is due to your secret newly-discovered physics (which excludes greenhouse effects).
(The incident sunlight i.e. solar irradiation at Venus is amost exactly twice that at Earth.)
Perhaps a double-header Nobel Prize is coming your way, CloudySky? You could also garner the Nobel Prize for Medicine, if you can show that Venus's feverish temperature is due to an . . . ah . . . ahem . . . Venereal condition.
I hope your legislators vote to cool the charade of global warming, by at least 1 degree.
[BL] The comment you responded to has been deleted, due to it being another incarnation of a banned user.
@MA Rodger 639
Sorry for taking so long to get back.
You said "The essential mechanism is that the CO2 greenhouse effect operates higher up in the atmosphere, above the bulk of of the atmospheric water vapour. Thus it is CO2 which determines the altitude from which the IR in this band is emitted into space, thus the amount of this IR emitted into space (determined by the atmospheric temperature of the point of emission) and thus it is CO2 which determines the amount of greenhouse warming from this waveband."
Could you explain what is the action of CO2 at those altitudes where the air is 1/10th the density and thus I guess there is a proportionate amount of CO2. With that little CO2 and the fact that it well might have lost a lot of energy by then, I don't understand how such a small amount of ~15um radiation is such a control factor for the whole atmosphere.
Thanks
[BL] You are again asserting things that make no sense.
Have you actually looked to see at what altitude the air density is 1/10th of the surface value? This is easy stuff to look up.
Early Google hit: https://www.engineeringtoolbox.com/standard-atmosphere-d_604.html
Density is 1/10 of surface value at an altitude between 30 and 40 km. The same table tells you that this is well into the stratosphere, where temperature is now decreasing with height. This is not "the upper atmosphere" that MA Rodger is referring to. The troposphere, where nearly all water vapour is found, is the first 10-12 km. In fact, most of the water vapour is found in the first few km. You are off by an order of magnitude.
You are also acting (again) as if 15um is the only wavelength of importance. It is not. And the upper atmosphere (troposphere) is not working in isolation. It is linked to the rest of the atmosphere. Scientists look at this in its entirety - not as isolated compartments of tidbits of information.
You can use this link to MODTRAN to examine how different parameters and variables affect IR radiation transfer. You would be far better off using your time to experiment with that web site and try to answer your own questions.
Until you learn how the atmosphere works as a system, you will continue to fail to understand these issues. I suggest that you get yourself an introductory climate and/or weather text book suitable for an undergraduate program, and read it.
I looked up the preassure at the tropopause. My bad assumption that that was the altitude of water. The chart said .1 bar. Pressure at sea is 1 bar. Your chart shows 2km. I agree. I still have the question about how does CO2 in such small amounts, .04%, act as the control knob for the atmosphere when water is so completely overwhelming? Is CO2 more populated above 2km? And I add at any altitude. It doesn't hold the energy. It loses it to surrounding air very rapidly, if it happens to get hit with a photon. Where is the emperical evidence or laboratory experiment that proves it has caused the increase in temperature? I read your page at https://skepticalscience.com/CO2-trace-gas.htm. No emperical evidence just a loose correlation and assumption that because temp went up 1.5F since 1880 and CO2 concentration went up that CO2 caused the increase in temperature. Recent temperatures have been flat or falling since 2015 and CO2 concentration has continued to climb.
[BL] Confusion between air pressure and air density would be avoided by reading pretty much any introductory meteorology text.
You ask how CO2 absorbing photons heats the atmosphere, while in the same breath saying that the energy is lost to the surroundings. Exactly. The energy gets added to surrounding molecules by collision, so the entire atmosphere at that location gets heated. In turn, a more heated atmosphere has more energy, and when energy is transferred to GHG molecules by collision with other molecules, the GHG molecules will sometimes emit that energy as radiation. Those are the fundamentals of radiative transfer in the atmosphere. Then, climate scientists add in all the other energy transfers involved (atmospheric motions, evaporation, condensation, etc.), and - gee golly - adding CO2 causes warming.
You can read about this absorption process in detail over at Eli Rabett's blog.
As for temperatures: you link to a site that says "It uses unadjusted surface temperatures." The site gives absolutely no indication on that main page how it handles spatial representation of individual stations, or how varying station numbers or locations affect the result over time. Adjustments are absolutely necessary to account for instrumentation, location, and sampling changes. THe source of data they use - METARS - is real-time weather observations, which have not gone through much QA/QC to weed out bad data. Without this information, it is impossible to know the validity of the analysis and methodology. Honest scientists publish the methodology they use.
Recently, in response to another comment here, I posted a link to RealClimate's analysis of observed temperatures versus model predictions. They provide an image that includes four reputable global temperature analyses:
The only way you can get "no warming since 2015" is by cherry-picking a peak in the noise. By the same methodology, I could say "oh, my, look at how fast it has been warming since 2017!!!". The same "no warming..." claims were being made in the years after 1998 (a huge El Nino year) - until it became obvious that warming was continuing. Then when the post-2015 period came along, the fake skeptic industry appeared to do a search-and-replace, substituting 2015 for 1998. You don't do trend analysis on a noisy by cherry picking a peak (especially one from a known cause - no more than you would conclude that the tide is no longer rising because the water level on the beach isn't as high as it was at the crest of the last wave.
Guess. what? We have a page on that, too.
And we have a graphic and a name for the tactic: the Escalator. (It's down the right hand side of every page here.) You can read about how the graphic is constructed here.
I've done it again. I'll move any other questions to https://skepticalscience.com/water-vapor-greenhouse-gas.htm
Likeitwarm @654&655,
My comment @639 was specifically tailored and indeed a little nuanced to keep discussion within the thread's topic. So straying beyond that topic in a response would not be unsurprising.
One point to make is that the pressure at the tropopause is usually given as a fifth of surface pressure (200 hPa) and certainly not a tenth. And its altitude commonly given as 12km.

But more exactly, the tropopause changes in height and pressure a lot by latitude and also a bit by the seasons. It can be as high as 17km with pressures down to 110 hPa over the tropics and as low as 8km over the poles with pressures up to 310 hPa.
CO2 is well mixed in the atmosphere up to the top of the stratosphere at 50km altitude. (The bulk of atmospheric water vapour rains out low down in the troposphere, as demonstraed by the moderator-appended graphic @654.)
You still seem concerned that high up in the atmosphere, the CO2 at altitude is well spread out as the pressure falls (so about a fifth the density at the tropopause) and also colder so there would be less thermal energy.
And it is fundamentally this reduction in energy with altitude that drives the greenhouse effect.
The greenhouse effect is all about the altitude at which upward-emitted IR can find holes inbetween the greenhouse gases above**, allowing the IR to escape from the atmosphere and exit into space.
If that altitude were low down, the atmosphere will indeed be relatively warm and thus thermally energetic. This energy means the CO2 gets a lot of the thumping from air mollecules that sends it into the flap that can emit IR in the 15 micron wave band. And warmer air at this emissions altitude means there is a lot of the flapping CO2 at the emission altitude and thus a lot of IR pouring through the holes into space, cooling the planet.
Note this emission altitude will always have the same amount of CO2 above. It is this physical presence determines the altitude where those holes appear to allow IR into space.
When you then add CO2, the altitude with holes out to space becomes higher. And as the troposphere cools with altitude, and the air higher up is less energetic, it gives the CO2 less of a thumping, so with this dropping temperature there is less CO2 flapping and so there is less IR pourng out into space because of that additional CO2. That means less cooling so the planet will have to warm to find a new hotter equilibrium temperature.
And don't think of this reduction as a small effect. There is 3,000,000,000,000 tons of CO2 in tha atmosphere and ~20% of it (so 600 billion tons) is up there playing a planet-warming game of 'catch the photon' high in the upper troposphere and today shooting something like 5,000TW out into space. (By comparison, today mankind's global primary energy use is 18TW.)
Add more CO2 and it will still be the top 600 billion tons of it playing that game of catch, but being now higher and thus colder, playing it with a little less vigour and so shooting a little less out into space.
(** The emission altitude isn't constant across the 15 micron wave band. The very centre of it, a narrow band on 15 microns, emits into space from way up in the stratosphere while the outer edges of the wave band still allow IR into space low down in the troposphere. These all move upwards with extra atmospheric CO2.)
@MA Rodger 657
Again, my apologies for going off topic.
Thanks for the lengthy and indepth explanation. I don't think I have seen such an explanation anywhere else I've looked. I think it should be more prominently displayed for those like myself who do not understand how GHG's work to warm the atmosphere.
It'll take me a 7 days of studying and contemplating your explanation, but I'm sure to have better understanding then.
Best to you.
[BL] I have added a lengthy moderators comment to your earlier post.
GreenEarth @659 :
In general, a CO2 molecule radiates a 15 micron photon after gaining energy from impact with a neighbouring O2 or N2 molecule. This type of impact happens at all levels of the troposphere/stratosphere. (The similar mechanism also applies with all the other greenhouse gasses.)
Therefore your stated supposition about altitude and radiation of photonic energy is entirely wrong. (But I am curious where you got such an erroneous idea from. Can you elaborate? )
[BL] Snipped portions that are a direct response to a deleted comment
Note that this issue of absorbed radiation being transferred to other molecules has been discussed recently in this thread. A detailed explanation of at Eli Rabbet's was previously pointed out in the moderation comments on comment 655.
GreenEarth @659,
The quote from the 'Advanced' rebuttal you make continues:-
And this is then followed by description of a simplistic model of a spreading absorption band caused by increased CO2. (It isn't perhaps the best of descriptions but the physics is both complex and novel for general consumption so what is 'best' will always be debatable.)
The continuation of your quote is saying that it the altitude from which IR is emitted into space that is the important, this being the effective radiative "top of the atmosphere".
And adding more CO2 (which is well-mixed up to the top of the stratosphere at 50km) puts more high-up CO2 in the way of the IR that would previously have exited to space. So more CO2 pushes the CO2 "TOA" further up not lower down.
If you consider the additional CO2 near the surface, more CO2 does indeed reduce the path length of IR before it encounters a CO2 molecule to absorb it. But because CO2 both emits and absorbs IR in equal measure**, while the IR has a shorter path length, with added CO2 more IR is being emitted. At a constant temperture, the shorter path length and the increased emissions cancel out. (**As Eclectic @660 says, CO2 emits due to collisions with other air mollecules. These collisions also absorb the energy from almost all absorbed IR. Because of this, the level of IR emission is determined by temperature and not by IR emissions from the surface.)
[BL] Note that this is a response to deleted comment.
Hi GreenEarth (@661) ,
Offhand, I am not sure which would be the best page here to point you to ~ IIRC this information can be found on a number of threads (and perhaps a kindly Moderator can indicate some suitable ones).
What we are talking about is very basic stuff known by all physicists having any connection with radiation & atmosphere (in other words, climate science).
In short, the atmospheric molecules are all knocking about against each other. Likewise for the various molecules of the Earth's surface ~ energy passes from surface to atmosphere, and vice versa, by these impacts. There is also bi-directional energy exchange between the planetary surface and adjacent air, via radiated photons. (Of course, there is also short-wave photonic energy coming from the sun ~ including from clouds, dispersion by dust etcetera in the air.)
The surface loses "heat" upwards by convection, by evaporation/condensation, and by radiation (mostly by radiation into the atmosphere, but a small amount by direct radiation out to space via the "window" band around 10 microns). The so-called "sensible heat" loss (producing warm air and thus convection) derives from molecular impacts as well as the limited-range radiation you have mentioned earlier.
Once the energy has risen to the so-called Top Of Atmosphere [TOA] it can then be radiated out into space (the TOA altitude level is different for CO2, H2O, CH4 , and other greenhouse gasses).
I hope I have not been repeating too much stuff that you already know.
The essential point is that because the greenhouse gas molecules are so thinly distributed among the bulk of N2/O2 air molecules, they are speeding/ slowing/ vibrating owing to impacts with the N2/O2 molecules which are moving at the (average) speed determined by the local air temperature. In effect, CO2 [for example] is able to broadcast 15 micron photons by gaining energy from local air (and by radiating, effectively cools the adjacent air). Almost all the energy for radiation comes from impact energy ~ and only a minuscule amount is contributed from a received/absorbed 15 micron photon from a "distant" CO2 molecule.
This is the reason why the concentration of CO2 at near-surface altitude is irrelevant to the greenhouse warming effect ~ because the concentration at TOA is the important determiner of the planetary effect. Then we get to the importance of the temperature at TOA and the actual altitude at TOA combined with the Lapse Rate temperature gradient.
GreenEarth, my apologies if my condensed explanation is not as clear as you would like, but I hope it sets you off in a useful direction of exploration of the basic concepts. And I would be interested to know where the incorrect ideas you got were coming from.
[BL] Portions snipped. Note that this is a response to a deleted comment. The poster in question has been pointed to appropriate places may times, but has not shown a positive learning slope.
Thanks MARodger @662 ~ sorry to have cross-posted with you.
The more the merrier, I hope. As you indicate, the subject is not particularly intuitive, and I hope to learn something more from GreenEarth's previous experience at other internet sites.
[BL] Response to deleted comment
GreenEarth @661,
As Eclectic @ 663 says, your "mystery" is a 'phycisist' thing. You would get a reply from a physicist that it is well known that all thing which absorb photons likewise emit them. And to provide authority for such a statement they would cite Beer's Law.
This is true, but most folk would not find this entirely helpful.
Consider the specrum of light. It is well known to have absorption lines which provide the fingerprint of the gases which cause those apsorption lines. But these are identical to the less-well known emission lines of those gases, the lines being caused by the difference in temperature of the gases and the more distant 'background emitter'. If the gases are cooler than the background, the lines will show as absorpion. If the gases are hotter they will show as emitters.
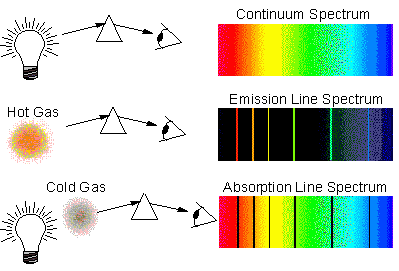
See also this 'Lesson Explainer' which may help.
At lower temperatures (and thus lower energies) where only IR is being emitted, the more simple molecules like N2, O2 & Ar are entirely transparent, neither absorbing nor emitting IR.

Greenhouse gases are more complex molecules so can waggle in more complex ways than mono- & bi-atomic molecules, these waggles defining the basic absorption wavelengths. Thus for CO2, the waggles, (top to bottom in the diagram) v1, v2 & v3, are caused by abrosbing IR at 2.7 microns, 15 microns and 4.3 microns. They are also caused (and in our atmosphere overwhelmingly so) by collisions with other air mollecules, collisions which also overwhelmingly de-waggle the CO2. A CO2 molecule getting the chance to de-waggle by emitting an IR photon is comparatively rare (although there is loads of CO2 molecules so IR is emitted).
Our atmosphere is too cold to give a strong enough bash to the CO2 to impart the v1 & v3 waggles, so it is only the 15 micron v2 that concerns us. The v1 waggle is induced in the atmosphere by sunlight which is just about still significant at 2.7 microns, but our atmosphere is not hot enough to create v1 waggles so there are no IR emissions at 2.7 microns. And by 4.3 microns the sunlight is entirely weak while the atmosphere is still too cold, so v3 falls between the terrestrial and solar energies and is absent here on Earth.
[BL] Note that comments have been moving around a bit due to deletions. Eclectic's comment 663 is now at 661.
Before anyone spends a lot more time on responses to some of these questions, it may be worth waiting to see if the comment survives moderation. We've seen a lot of thread-bombing on this particular subject in the past 2-3 months, seeing the same tired old "criticisms" of basic science. Although posed as questions, the commenter(s) rarely have any desire to learn the science.
TheSpook @664 ,
again and again in this thread, you seem to be struggling to understand the concept of saturation and its relevance to GHE. This is stuff which is in textbooks and it is straightforward, if you put your mind to it. And yet your thoughts seem locked in a futile circle of misunderstanding, and therefore you are wasting your time with excessive repetition.
Best if you start with a clean sheet ~ firstly define the term saturation (as you understand the meaning and significance of the term). Then link that to the concepts of the mechanism of GHE.
Somewhere, you yourself have a semantic and/or logical problem which is impeding your your understanding of what is basically a straightforward concept, namely GHE (of one or several gasses).
[BL] Response to deleted comment.
@666 , once again you demonstrate a disconnect from GHE concept.
The fault is not in your stars, but in yourself [excuse Caesar misquote].
Please start afresh. Forget "saturation". Look at the molecules, look at the intermolecular distances, look at the absorptions & radiations. Think about what is going on at that basic level. This is basic physics. This is reality. Scientists (excluding Angstrom) understand GHE because it is straightforward ~ when you stop to think it through.
[BL] Response to deleted comment.
@668 ,
you are mistaken ~ I do not object to your postings. They are entertaining to a certain extent, but do not rise above Bronze Medal for skill of disingenuousness.
[BL] Response to deleted comment.
Spooker @667 & many now evanescent posts :-
You are far too modest about your PhD in Physics (Acoustics, I hear?). And you are even more modest about your double Laureate ~ which is in the pipeline (as I hear, from friends in Stockholm).
Which all makes it so puzzling that your confidence you understand "saturation" (re GHE) seems in a clear contradiction to your evident failure to comprehend GHE.
(~ At least, as far as can be determined from your many posts.) But perhaps you can clarify why you think some form of "saturation" is relevant to GHE . . . and at the same time clarify how & why you are correct about GHE while the generality of atmospheric physicists are grossly wrong about GHE.
[BL] The comment in question has been deleted.
The commenter currently shown @667 and naming themself 'Spooker' claims to have been awarded a PhD in Physics and asks whether it should have occurred to others that perhaps 'Spooker' "already know(s) the basic science behind the GHE."
It is not unknown for those who are very well versed in Physics to be for some reason incapable of grasping the mechanisms of the greenhouse effect and deny it exists. William Happer was such a one (I think recently he has been used as a co-author in work that does present the existence of AGW but of a much diminished form, a la the likes of Dickie Lindzen), although he does have the excuse of being very old and, as the adage goes, 'you can't teach an old dog new tricks'.
What I would ask this commenter presently calling themself Spooker, and ask in a sciency-physics sort of way, if all the IR emitted by the planet surface is absorbed by the CO2 in the atmosphere above within metres of the surface (which for the central specrtum of the CO2 emissions spectrum at ~666cm^-1 is true) and thus cannot impact the planetary energy balance at the top of the atmosphere, where does all the other IR come from? For instance, what is the source of all the downwelling IR that can be seen by instruments on the surface.
The graphic demonstrating such measurement below was sourced from here.
[BL] Snipped portions that referred to a comment that has been deleted. Informative sections left intact.
It is easier to interpret radiant energy leaving the top of the atmosphere (TOA) toward space than to track it after being emitted from the surface. Radiant energy intensity as a function of wavelength depends only upon the composition and temperature of the emitting source. In other words, the emitted energy in the 14-16 micron band that is emitted to space comes from CO2 in the tropopause near the lower stratosphere. There are sufficient CO2 molecules in this layer to bring the emissivity to 1.0 and the temperature is about 220K. The TOA is the system boundary for the global energy balance. At most other wavelengths, CO2 has an emissivity of 0, so IR emissions are due to another substance which may or may not be emitting at a different temperature. That is why it is easier to explain IR loss to space by looking at the downward from the TOA instead of trying to track IR leaving the surface, which gets absorbed and re-emitted and re-absorbed and re-emitted again.
I see several previous references to MODTRAN in this thread. Great. It is an easy-to-use free, public access online program for modeling radiant energy in the atmosphere. The hardest part to grasp is that it is not an energy balance model that calculates the surface temperature, but a radiation model that calculates the radiant energy flow for a specified surface temperature and atmospheric temperature profile. Much can be learned from using it, including the saturation effect for CO2 and CH4, effect of water vapor and water vapor feedback, and radiant energy flow upward and downward through the atmospheric, and the importance of the atmospheric temperature profile for the greenhouse effect. Note that the saturation effect can be observed as widening the 14-16 micron trough with increasing CO2, while the depth of the trough is set by the emission temperature. While the saturation effect tends to be logarithmic, it has not plateaued for CO2. For CH4 at 18. ppm, any saturation effect has barely started. That is what makes CH4 such a powerful greenhouse gas.
The short answer to the question about downward IR is that it comes from radiated energy from GHG in the lower atmosphere. To fully understand the upward and downward flow of IR, try exercising MODTRAN at different altitudes and switch between looking at the spectrum upward and downward.
Charlie_Brown:
One minor clarification. You say "Radiant energy intensity as a function of wavelength depends only upon the composition and temperature of the emitting source."
Yes, this is correct for radiant energy emitted locally, but when it comes to measuring radiant energy at a point, you get both the locally-emitted energy plus any energy at that wavelength that was emitted elsewhere and has been transmitted through the atmosphere to that point - i.e., it has not been absorbed by the intervening atmosphere. At some wavelengths, where atmospheric absorption is large, it will be mostly locally-emitted. At wavelengths where atmospheric absorption is small, it will be mostly transmitted from elsewhere.
The complication that you refer to in terms of what is seen at any particular height in the atmosphere is that it includes both components (local emission plus transmission). From measurements of radiant energy alone you cannot know how much is from each. For that, you need models that incorporate temperature, all gases and their emission spectra, etc.
And, as you state, models such as MODTRAN will do that for you - but they are not energy balance models. You need to specify the temperature profile (and cloud profile, and gases) and then you can get the profile of radiative energy (upward and downward fluxes, absorption and emission rates).
If that radiative energy transfer does not balance (local absorption and emission are not equal), then locally you will have either heating or cooling. At that point, you can iteratively warm or cool that layer (and all other layers), recalculate the temperature profile, recalculate the radiative transfer, etc until you find a temperature profile that is at equilibrium.
And people have done this. Classic early references are from roughly 60 years ago (and have been linked to earlier in this long comments thread).
Manabe and Strickler 1964
Manabe and Wetherald 1967
If you only consider radiatve transfer, the atmosphere would stabilize at a much steeper temperature gradient than exists. If you adjust for this (Manabe et al's "convective adjustment") you get a very good fit to actual global mean temperature. Figure 1 from Manabe and Strickler shows these two scenarios clearly, as well as the iterative process of radiative calculations, determining heating/cooling, radiative calculations, etc:
An interesting paper appeared in BAMS earlier this month, looking at the historical importance of this early work by Manabe.
Certain stubbornly-ignorant self-proclaimed experts that have repeatedly invaded this thread seem to lose sight of the fact that the atmosphere also emits radiation in the wavelengths that are strongly-absorbed. It's easy to deny that the Greenhouse Effect exists if you deny that CO2 is a strong emitter as well as a strong absorber.
[BL] Due to a recently-noted bug in the SkS code, the link to this comment, as it appears in "Recent Comments" will take you to the wrong page. For the convenience of anyone trying to follow the thread, here is the correct link (note the p=27 part):
https://skepticalscience.com/argument.php?a=82&p=27#139813
Further minor note:
The radiative-convective model work of Manabe et al does include both IR radiative transfer and solar radiation. This is necessary for a proper energy balance model. The stratospheric heating seen in the above figures is largely due to ozone absorption of UV radiation.
MODTRAN, as linked to earlier in comments, focusses on IR radiation.
Bob Loblaw
Good clarifications, thank you. I should have said “Emitted radiant energy intensity as a function of wavelength depends only upon the composition and temperature of the emitting source.”
Also, thank you for the references to Manabe’s work and to the BAMS paper. Manabe’s approach demonstrated the effect of stratospheric cooling and tropospheric warming from CO2 doubling. Since MODTRAN uses a specified atmospheric temperature profile, this version of the model can’t be changed to show this effect. One always needs to be mindful of the purpose and limitations of any model that is used.
Those who deny that “CO2 is a strong emitter as well as a strong absorber” should be reminded of Kirchhoff’s Law that absorptance equals emittance, although precisely only when there is thermodynamic equilibrium. This is a very good approximation in the atmosphere, but it means that any slight imbalance between photon absorptance and emittance will be manifested as a temperature change. Conservation of energy is rigorous, but not conservation of photons. This is one reason why tracking the path of photons emitted from the surface is problematic. The simple fact is that CO2 in the tropopause absorbs and emits radiant energy based on the cold temperature at that altitude.
Yes, the U Chicago link to MODTRAN I gave above does not allow you to enter in an arbitrary temperature profile. You can choose "Locality" from a pre-set list, and a variety of pre-set values for cloud and precipitation conditions. This will alter the temperature profile displayed on the right - but the online interface has its limitations as far as user preferences go.
The stratospheric cooling in response to increased CO2, illustrated in figure 16 of Manabe and Wetherald 1967 (linked in previous comments, but included here again for convenience) is largely due to more CO2 in the stratosphere emitting more IR at the same temperature, so the same outward IR flux to space can be accomplished at lower temperatures.
Great post and discussion! Thank you
I'm rather new to this and have been struggling with finding a sound rebuttal to the reasonable sounding claims in this paper. As far as I understand it there is a weak saturation-claim to be found here:
Link to van Wijngaarden and Happer paper
thanks!
[BL] Glad that you found the relevant discussion in the comments.
Created a link to the paper. The web software here does not automatically create links. You can do this when posting a comment by selecting the "insert" tab, selecting the text you want to use for the link, and clicking on the icon that looks like a chain link. Add the URL in the dialog box.
I've just seen a discussion of this from post 587 onwards...
[BL] Here is a direct link to comment 587 in this thread.